© h.hofstede (h.hofstede@hogeland.nl)

De ζ-functie.
       
De zeta-functie (meestal geschreven als  ζ(s))  is erg eenvoudig gedefinieerd. Zeg maar gerust verraderlijk eenvoudig:
       

       
Dus dan krijg je dit soort dingen:
       

enzovoort.
Laten we de functiewaarden langzaamaan één voor één gaan onderzoeken....
 

ζ(1) = ∞
   

Dat de reeks voor s = 1 divergeert was al ongeveer vanaf 1350 bekend.

Dat het inderdaad klopt kun je makkelijk zien door de termen te gaan groeperen.

Doe dat als volgt:
       
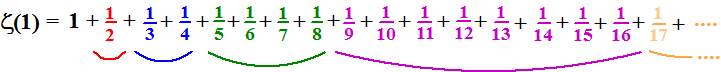Vanaf de 1/2 neem je groepjes van 1 (rood) , 2 (blauw), 4 (groen) , 8 (paars), 16 (oranje) ... termen bij elkaar.
• Het blauwe groepje bestaat uit twee termen die beiden groter dan of gelijk aan 1/4 zijn (want 1/4 is de kleinste), dus samen is dat groter of gelijk aan 2 • 1/4 = 1/2
• Het groene groepje bestaat uit vier termen die allen groter dan of gelijk aan 1/8 zijn (want 1/8 is de kleinste), dus samen is dat groter of gelijk aan 4 • 1/8 = 1/2
• Het paarse groepje bestaat uit acht termen die allen groter dan of gelijk aan 1/16 zijn (want 1/16 is de kleinste), dus samen is dat groter of gelijk aan 8 • 1/16 = 1/2
En zo gaat dat alsmaar door.
De hele reeks wordt dan groter of gelijk aan 1 + 1/2 + 1/2 + 1/2 + .....  en dat wordt inderdaad oneindig groot.

De convergentie van deze reeks is ontzettend sloom. Na 10 miljard termen zijn we pas gekomen tot nog niet eens 24. Om 100 te halen heb je ongeveer 15000000000000000000000000000000000000000000  termen nodig!!!
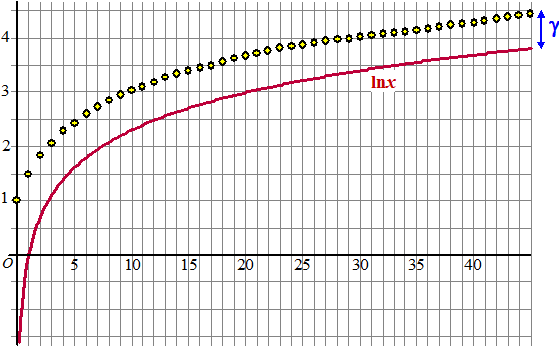
Euler toonde zo rond 1750 aan dat deze reeks ongeveer even snel verloopt als de natuurlijke logaritme ln(n).
       

       

Het verschil tussen beide grafieken wordt constant:  de beroemde constante van Euler:  γ
Dat is, na π en e,  misschien wel de belangrijkste wiskundige constante is die bestaat.
       
γ = 0,577215664901532......
       
ζ(2) = 1/6π²
       
Het berekenen van z(2) is meteen een flink stuk moeilijker dan ζ(1). Pas in 1734 kwam de oplossing. Van niemand anders dan ...... Euler natuurlijk!!

Een prachtig stukje wiskunde.

Euler begon met de reeksontwikkeling voor sinx:

En toen had hij een geniale ingeving:  hij dacht "Als ik nou x vervang door √x dan worden die machten van x groter met in plaats van 2 machten per stapje nog maar met 1 macht per stapje". Om de machten mooi geheel te maken, bekeek Euler de reeksontwikkeling voor  sin√x/√x :

Oké;  mooi oplopende machten, maar wat heb je eraan?

Het mooie komt als je de nulpunten van sin√x/√x gaat opsporen.
Dat is nul als  √x = π, 2π, 3π, 4π, .....  dus dan is x = π2 , 4π2, 9π2, 16π2, .....  (niet bij x = 0  want  sinx/x gaat naar 1 voor x naar 0)
Dus moet dat polynoom daar ook de nulpunten hebben.
Dan kun je dat polynoom schrijven als   (1 - x/π²) • (1 - x/4π²) • (1 - x/9π²) • (1 - x/16π²)    ....    (dat zegt de factorstelling, want de eerste term van de reeks is 1)
Laten we beginnen de haakjes weg te werken, vanaf links. Let daarbij vooral op de termen waar een x in komt
   (1 - x/π²) • (1 - x/4π²) • (1 - x/9π²) • (1 - x/16π²).... 
= (1 -  x/π²  - x/4π² + hogere machten van x ) •  (1 - x/9π²) • (1 - x/16π²).... 
= (1 -  x/π²  - x/4π²  - x/9π²  + hogere machten van x ) •  (1 - x/16π²).... 
enz.
       
De coëfficiënt van x wordt gelijk aan  -(1/π² + 1/4π² + 1/9π² + 1/16π² + ....)
Maar volgens de reeksontwikkeling van sin√x/√x  moet dat gelijk zijn aan  -1/3! = -1/6
-(1/π² + 1/4π² + 1/9π² + 1/16π² + ....) = -1/6
1 + 1/4 + 1/9 + 1/16 + .... = 1/6π2
ζ(2) = 1/6π2  

Mooi toch?
       
ζ(4) en ζ(6) en ζ(8) en...
       
Die zijn een stuk lastiger........
Meer iets voor een  volgende les.......
       

© h.hofstede (h.hofstede@hogeland.nl)