Machtsfuncties.

© h.hofstede (h.hofstede@hogeland.nl)

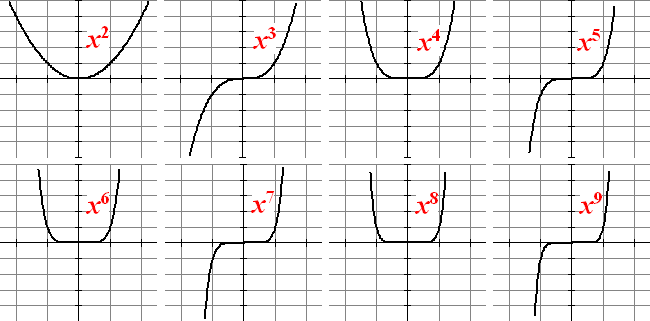
We beginnen met het plotten van de grafieken van y = x2, y = x3, y = x4 , y = x5  enz.:

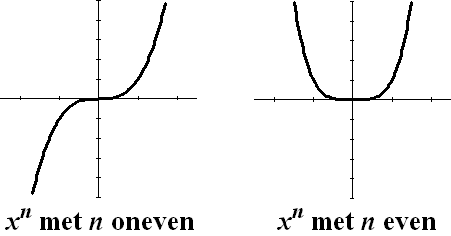
Het patroon is wel duidelijk, denk ik: de even machten (x2, x4, x6 , ...)  hebben allemaal een soort van dalparabool-vorm en de oneven machten  (x3, x5, x7, ...) hebben de vorm van een soort "golfje". Dat is ook nogal logisch als je het volgende bedenkt:
• De grafieken gaan allemaal door (0,0).
• Voor hele grote x-waarden wordt y ook heel groot, dus aan de rechterkant schieten de grafieken omhoog.
• Voor grote negatieve x-waarden worden de oneven machten ook negatief maar de even machten positief.
De oneven grafieken lopen dus aan de linkerkant omlaag en de even omhoog.

Wat zijn de gevolgen?
De vorm van deze grafieken heeft gevolgen voor het oplossen van vergelijkingen.
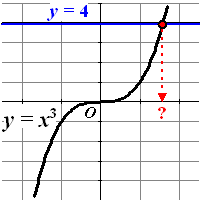
Als we bijvoorbeeld de vergelijking x3 = 4 proberen op te lossen, dan zoeken we eigenlijk het snijpunt van de lijn y = 4  met de grafiek van y = x3 .
In de figuur hiernaast vind je de oplossing bij het rode vraagteken.

Uit de lessen over het rekenen met machten weten we al dat :
xn = p   ⇒  x = p1/n

In dit geval is de oplossing dus  x = 41/3    (≈ 1,5874...)

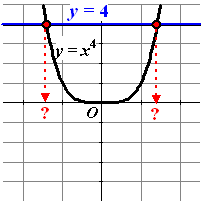
Maar kijk wat er gebeurt bij even machten.
Als we op dezelfde manier proberen op te lossen x4 = 4 dan geeft dat de grafiek hiernaast.

En nu zijn er ineens TWEE oplossingen!
Dat komt natuurlijk omdat een negatief getal tot de vierde macht ook weer positief wordt, dus ook 4 kan opleveren.
Die oplossingen zijn  x = 41/4  (≈ 1,4142...)  maar ook  x = -41/4 (≈ -1,4142...)
Het vervelende is, dat we met de regel xn = p   ⇒  x = p1/n  maar één oplossing vinden (de positieve). Er zit niets anders op: We moeten gewoon zelf onthouden dat er een tweede oplossing is bij even machten.

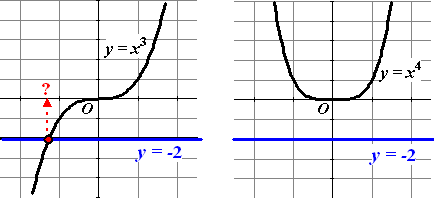
Die even machten zijn maar vervelende dingen, want er is nóg een complicatie.
Dat zie je als je probeert op te lossen xn = p met p een negatief getal.  Hieronder staan grafieken die horen bij x3 = -2 en x4 = -2.

Links zie je dat er bij x3 = -2 geen problemen zijn: er is gewoon één oplossing en dat is  x = (-2)1/3   (≈ -1,2599...)
Maar rechts zie je dat die even machten alwéér ellende geven: er is geen oplossing.
Dus de oplossing die je zou verwachten:  x = (-2)1/4   Die bestaat helemaal niet!!!

Samengevat:

xn = p
 
Als n oneven is: één oplossing
Als n even is: als p > 0
als p < 0		 twee oplossingen
géén oplossing
   
OPGAVEN
1. Los op:
a.  x5 = 8

81/5
f.   x3 + 4 = 5x3 + 16

(-3)1/3
b.  x6 = 7

71/6 of -71/6
g.  6x10 - 8 = 4

20,1 of -20,1
c.  4x8 = 64

161/8 of -161/8
h.  x5 + 12 = -x5 + 2

-50,2
d.  2x4 + 6 = 0

geen opl.
i.   0,5x6  + 4 =  1

geen opl.
  e.  3x3 + 8 = 2

(-2)1/3
j.   0,1x4  - 3 = 2

501/4 of -501/4
       
   

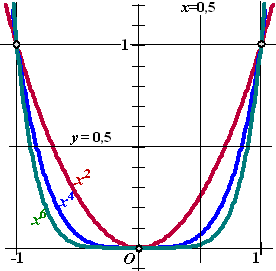
2.

Hiernaast staan de grafieken van y = x2 en y = x4 
en  y = x6 getekend. Zoals je ziet gaan ze allemaal door (0,0) en (1,1) en (-1,1)

     
  a. Hoe lang zijn de stukjes van de lijn  y = 0,5 die zich tussen de grafieken van y = x2 en y = x4 bevinden?
Geef je antwoord in 3 decimalen.
 

elk 0,134
b. Hoe lang is het deel van de lijn  x = 0,5 dat zich tussen de grafieken van y = x4 en y = x6 bevindt?
 

3/64
Als je de rij grafieken zou uitbreiden met x8, x10 , enz. Dan zijn er twee opeenvolgende grafieken zodat het deel van de lijn x = 0,5 dat zich tussen deze grafieken bevindt minder is dan 0,001.
 
c. Voor welke twee opeenvolgende grafieken is dat voor het eerst zo?

x9 en x10
 
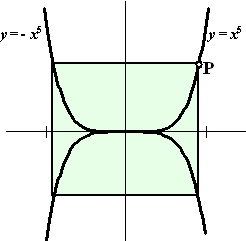
3. Hiernaast staan de grafieken getekend van y = x5 
en  y = -x5 getekend.
Vanaf een punt P op de grafiek van y = x5 wordt een rechthoek getekend als in de figuur hiernaast.

Als de x-coördinaat van P gelijk is aan p dan is de oppervlakte van deze rechthoek gelijk aan  4p6

     
  a. Toon aan dat dat klopt.
   
  b. Voor welk punt P is de oppervlakte van deze rechthoek gelijk aan 12?  Geef je antwoord in twee decimalen.
 

p ≈ 1,20
       
4. Stel dat bekend is dat de ongelijkheid  g1 • g2 • ... • gn  < 1/5   juist is als  n > 4 en niet juist als n ≤ 4 
Welke waarden kan g dan hebben?
Geef een algebraïsche berekening, en je antwoord in vier decimalen nauwkeurig.
     

g > 0,7647
       
5. Examenvraagstuk HAVO Wiskunde B, 2002
       
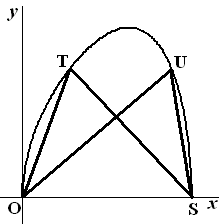
  Gegeven is de functie  f (x) = √(27x - x4)
De grafiek van  f  heeft met de x-as twee punten gemeen; de oorsprong O en een punt S.
Op de grafiek van f liggen twee punten T en U zodanig dat de oppervlaktes van driehoek OST en van driehoek OSU gelijk zijn aan 6.
Zie de figuur hiernaast.

     
  Bereken de coördinaten van T en U. Rond in je antwoord getallen die niet geheel zijn af op twee decimalen.
     

2,77 en 0,60
       
6. We bekijken in deze opgave de massa van een aantal kubussen met straal r

De massa MH van een houten kubus wordt gegeven door  MH = 0,6r3
De massa MD van een  draadmodel van een kubus wordt gegeven door  MD = 2,4r
De masse MP van een holle kubus van plexiglas wordt gegeven door  MP = 1,2r2
       
  a. Bereken bij welke ribbenlengte de kubus van plexiglas dezelfde massa heeft als de kubus van  hout.
     

1,59
  b. Bereken bij welke ribbenlengte de massa van de houten kubus de helft is van het draadmodel.
     

0,58
  c. Leg uit waarom de machten in de formules logisch zijn.  
       
7. Examenopgave VWO,Wiskunde A, 2018-I  (gewijzigd)

Sommige mensen hebben een schildpad als huisdier. Bepaalde soorten houden onder natuurlijke omstandigheden een winterslaap. De eigenaar kan ervoor kiezen om zijn schildpad ook in winterslaap te laten gaan, omdat hij anders de hele winter extra licht en warmte moet geven aan zijn huisdier. Een schildpad moet een gezond gewicht hebben bij het begin van zijn winterslaap, anders is er een kans dat hij het niet overleeft. Om vast te stellen of de schildpad een gezond gewicht heeft, wordt vaak de Jackson Ratio gebruikt.

De Jackson Ratio R wordt berekend met de formule  R = G/L³

Hierin is G het gewicht van de schildpad in gram en L de lengte van het schild van de schildpad in cm.
Voor de Griekse landschildpad geldt de volgende vuistregel: een schildpad kan veilig aan een winterslaap beginnen als zijn Jackson Ratio tussen 0,18 en 0,22 ligt.

Jesse heeft een Griekse landschildpad met een gewicht van 700 gram en wil hem een winterslaap laten houden.
       
  a. Bereken in mm nauwkeurig tussen welke waarden zijn schildlengte dan mag liggen volgens de vuistregel.
     

147 - 157
  De lengte van het schild moet recht gemeten worden, bijvoorbeeld door de schildpad met ingetrokken kop tussen een schuifmaat te zetten (zie foto 1). Veronderstel dat iemand toch de lengte over het schild heen meet (zie foto 2).
       
 

       
  b. Beredeneer of een schildpad door op die manier te meten een grotere of een kleinere Jackson Ratio krijgt dan hij in werkelijkheid heeft.
       
 

Op een Engelse website staat het volgende: als je het gewicht meet in Engelse ponden (lbs) en de schildlengte in inches, kun je de Jackson Ratio berekenen met de formule  R = c • W/l³

Hierin is W het gewicht in Engelse ponden en l de schildlengte in inches.
1 Engels pond (lb) ≈ 454 gram en 1 inch = 2,54 cm.
De Jackson Ratio moet dan ook weer dezelfde waarde opleveren.
       
  c. Bereken de waarde van c in deze formule. Rond je antwoord af op één decimaal.
     

27,7
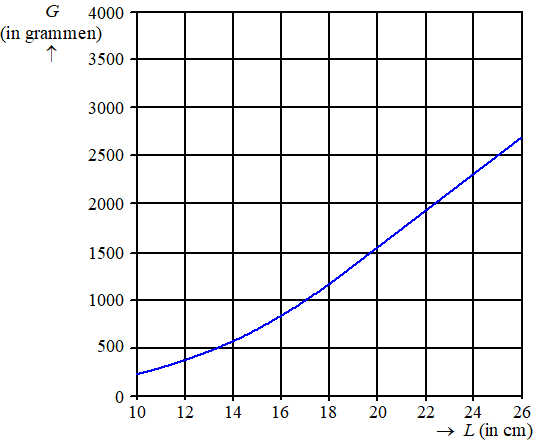
  Een andere manier om te bepalen of een Griekse landschildpad veilig aan een winterslaap kan beginnen, is met behulp van de grafiek in onderstaande figuur. De grafiek geeft het gewicht van gezonde schildpadden als functie van de schildlengte. Als een schildpad met zijn lengte en gewicht in de buurt van deze grafiek zit, is het veilig om hem in winterslaap te laten gaan.
       
 

       
  We vragen ons af of de grafiek van de figuur bij benadering overeenstemt met de eerder genoemde vuistregel. Om dit te onderzoeken kunnen we in de figuur de grafieken tekenen van de onder- en de bovengrens die horen bij de eerder genoemde vuistregel en vervolgens het gebied dat hoort bij die vuistregel in de figuur aangeven.
       
  d. Geef in de figuur het gebied aan waarin een schildpad zich volgens de vuistregel met zijn schildlengte en gewicht moet bevinden om veilig aan een winterslaap te kunnen beginnen.
     

© h.hofstede (h.hofstede@hogeland.nl)