| |
|
|
|
| 5. |
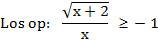 |
| |
|
|
|
| |
|
|
|
| 6. |
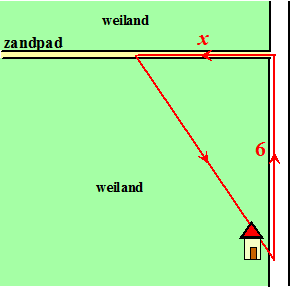
Een hardloper loopt elke week een
zelfde soort rondje.
Hij begint vanaf zijn huis met en stuk van 6 km over een
verharde weg.
Dan slaat hij linksaf (90°)
en loopt een stuk van lente x km over een zandpad.
Op een gegeven moment heeft hij daar genoeg van, en loopt hij
direct in een rechte lijn door het weiland terug naar zijn huis.
Voor de totale gelopen afstand geldt dan
A = x
+ 6 + √(36 + x2) |
 |
| |
|
|
| |
a. |
Toon dat aan. |
| |
|
|
| |
b. |
Bereken algebraïsch welke afstand de loper over
het zandpad moet lopen om in totaal 24 km te lopen. |
| |
|
|
| |
|
|
|
| 7. |
Als je een voorwerp van een toren
met hoogte 51 meter naar beneden laat vallen, dan geldt voor de
valtijd t (met t in seconden en t = 0 op het
moment van loslaten) als functie van de hoogte h (in
meters) de volgende formule:
t = √(10,20 - 0,20h) |
| |
|
|
|
| |
a. |
Hoe hoog is het voorwerp na 2 seconden? |
|
| |
|
|
|
| |
b. |
Na hoeveel seconden bereikt het
voorwerp de grond? |
| |
|
|
|
| |
c. |
Ook voor een toren met hoogte 80
meter geldt een formule van de vorm
t =
√(a - 0,20h)
Bereken de waarde van a bij deze toren. |
| |
|
|
|
| |
|
|
|
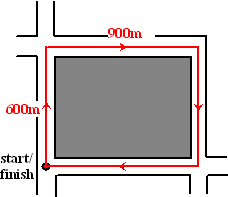
| 8. |
Bij een
hardloopwedstrijd moeten de deelnemers een aantal rondjes lopen.
Het rechthoekige parcours zie je hiernaast. De start en finish
zijn op dezelfde plaats. Eén rondje is precies 3 km.
Een bepaalde loper loopt zijn eerste rondje met een gemiddelde
snelheid van maar liefst 18 km per uur. Voor zijn afstand s
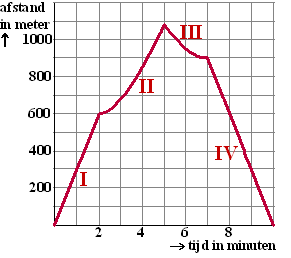
(hemelsbreed) tot de start/finish geldt tijdens dat rondje de
grafiek hiernaast (onder). Daarin staat de tijd in minuten en de afstand
in meter.
Zoals je ziet bestaat de grafiek uit drie delen. |
 |
| |
|
|
|
| |
a. |
Leg uit hoe je uit die grafiek kunt afleiden
dat
zijn snelheid inderdaad 18 km/uur is. |
 |
| |
|
|
| |
Voor deel II geldt de formule:
s = √(90000t2
- 360000t + 720000) |
| |
|
|
| |
b. |
Toon dat aan. |
| |
|
|
| |
c. |
Bereken algebraïsch wanneer de afstand van de
atleet tot de start voor het eerst groter is dan 800 meter
geef je antwoord in seconden nauwkeurig. |
| |
|
|
| |
|
|
|
| 9. |
Kleine
Laurens groeit als een wortel.
Letterlijk in dit geval, want zijn lengte L wordt gegeven door: L
= 16 • √(t + 9)
daarin is t in maanden met t = 0 als tijdstip van zijn
geboorte, en L in cm. |
| |
|
|
|
| |
a. |
Welke invloed
heeft het getal 9 op de grafiek van L? |
| |
|
|
|
| |
b. |
Bereken
algebraïsch wanneer Laurens 100 cm lang zal zijn. Rond je antwoord af op
twee decimalen. |
| |
|
|
|
| |
|
|
|
| |
Op de
geboortedag van Laurens heeft zijn trotse vader een boompje in de
tuin geplant. Dat boompje was toen 60 cm hoog. Het boompje groeit
lineair en zal na twee jaar 69,6 cm hoog zijn. Laurens is dan langer dan
het boompje. |
| |
|
|
|
| |
c. |
Hoeveel procent
is Laurens op dat moment langer dan het boompje? |
| |
|
|
|
| |
d. |
Stel een formule
op voor de lengte van het boompje en bepaal daarna op welk tijdstip
Laurens en het boompje even lang zijn. |
| |
|
|
|
| |
|
|
|
| 10. |
Examenopgave.
Door
stijging van de gemiddelde temperatuur op aarde worden gletsjers steeds
kleiner. Het ijs verdwijnt van plaatsen die eeuwenlang door de gletsjer
waren bedekt. Waar het ijs is verdwenen ontstaan vaak korstmossen. Met
behulp van deze mossen is het vaak mogelijk bij benadering het jaartal
te bepalen waarop het ijs verdwenen is. De mosgroei treedt min of meer
cirkelvormig op en er is een duidelijk verband tussen de diameter van
het mos en de leeftijd. Hoe groter de diameter van het mos, hoe ouder
het mos is, en dus hoe langer het geleden is dat die plaats nog door een
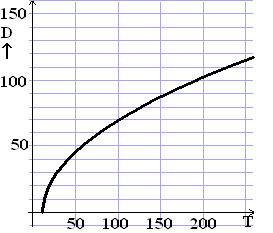
gletsjer was bedekt. Op grond van een aantal metingen is de grafiek
hiernaast getekend.
Deze grafiek geeft een verband tussen het aantal jaren (T in jaren) dat
een plaats ijsvrij is en de diameter (D in mm) van het korstmos op die
plaats. |
 |
| |
Een formule die het verband beschrijft is D = 6,9 • √(T
- 12)
De grafiek hiernaast en de formule geven voor T = 100
verschillende diameters.
|
| |
|
|
|
| |
a. |
Bereken
hoeveel procent de diameter uit de formule afwijkt van de diameter uit
de grafiek. |
| |
|
|
|
| |
b. |
Bereken
exact hoeveel jaar een plaats waar het korstmos 82,8 mm diameter heeft
volgens de formule ijsvrij is. |
| |
|
|
|
| |
Volgens
een ander model begint de diameter van het korstmos te groeien 12
jaar nadat het ijs verdwenen is, maar is deze groei lineair met 0,8 mm
per jaar. |
| |
|
|
|
| |
c. |
Bepaal
voor welke diameter beide modellen hetzelfde aantal jaren
voorspellen. Doe dat zowel met de grafiek hierboven als met de
formule voor D. |
| |
|
|
|
| |
|
|
|
 |
 |
| |
|
|
|