| |
 |
|
Vergelijkbare rijen. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
Het idee er achter is eigenlijk
heel simpel:
Als twee rijen an en bn zich (wat
convergeren en divergeren betreft) op ongeveer dezelfde manier gedragen,
dan zal de verhouding tussen die rijen nooit oneindig groot of nul
worden.
Officieel: |
| |
|
|
|
| Als an en bn
twee rijen zijn met an, bn
> 0 |
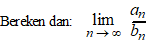 |
Als deze limiet positief en niet 0 of
¥ is, dan gedragen de
rijen an en bn
zich hetzelfde;
óf ze convergeren beiden, óf ze divergeren beiden. |
|
|
| |
|
|
|
Bewijs.
Noem die limiet L, dan komt (vanaf bepaalde n) de waarde
van an/bn dus willekeurig
dicht bij L te liggen. |
Op een getallenlijntje in de
buurt van L ziet dat eruit als hiernaast.
Er zijn dan wel getallen k en g (kleiner en
groter dan L) te vinden zodat vanaf bepaalde n al
die an/bn in het groene
gebied van de getallenlijn hiernaast liggen.
Dus er zijn getallen k en g te vinden zodat geldt
k < an/bn < g. |
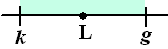 |
Maar dan geldt
k bn < an < g bn
Als bn nu divergeert, dan doet k bn
dat ook, en omdat an > k bn
divergeert an dan ook.
Als bn nu convergeert, dan doet g bn
dat ook, en omdat an < g bn
convergeert an dan ook.
Ze gedragen zich dus hetzelfde.
N.B.
Ik hoop dat je hebt gezien dat de rollen van an en
bn in dit hele verhaal volledig symmetrisch zijn. Bij de
opgaven mag je dus steeds zelf kiezen wat je an noemt
en wat bn. Dus welke de teller wordt en welke de
noemer. |
| |
|
|
|
| Voorbeeld. |
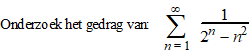 |
Als je daar zo naar
kijkt, dan vermoed je misschien wel dat die 2n de boel
gaat bepalen. Die wordt namelijk veel groter dan n2 .
Daarom vermoed ik dat deze rij vergelijkbaar zal zijn met de rij 1/2n.
Als je dat wilt onderzoeken, dan kun je kiezen uit twee breuken,
afhankelijk van welke je an noemt en welke bn:
|
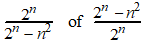 |
| Die tweede lijkt me
makkelijker, omdat je daar kunt uitdelen. |
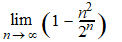 |
Maar dat laatste stuk
gaat naar nul (2n wint van n2) dus
uit de limiet komt 1.
Dat is een positief getal, en niet 0 of ∞ dus
de rijen zijn vergelijkbaar. Omdat we verder weten dat 1/2n
convergeert zal deze rij dat ook doen. |
| |
|
|
|
|
|