|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Omdat onze 3D-ruimte
nou eenmaal drie richtingen heeft, heb je dus ook voor een vector 3
kentallen nodig. Je moet om een "pijl" vast te leggen aangeven wat de verplaatsing in de x-richting, in de y-richting en in de z-richting is. Dat gebeurt (zo is nou eenmaal de afspraak) van boven naar beneden in deze volgorde. In deze les zullen we bekijken welke dingen die we al weten voor tweedimensionale vectoren nog steeds gelden, en welke veranderingen we moeten maken. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. De vectorvoorstelling van een lijn. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
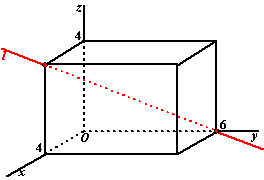
| Het basisprincipe is
gelijk: kies één punt als "beginpunt" (de steunvector) en tel daar een
aantal (l) keer een richtingsvector bij op. Hiernaast zie je een rode lijn l in een ruimtelijke figuur. Mogelijke vectorvoorstellingen van die lijn zijn: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
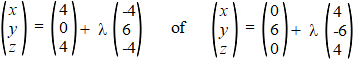| Een variabel punt van die lijn zou je kunnen weergeven door (4-4λ, 6λ, 4-4λ) of (4λ, 6-6λ, 4λ). Er zijn natuurlijk nog oneindig veel meer mogelijkheden.... | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. Lengte van een vector. Nog steeds niets nieuws onder de zon. Gewoon weer Pythagoras, alleen nu met 3 kentallen in plaats van 2. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
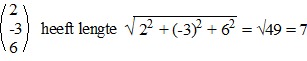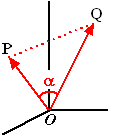
| 3. Inproduct en hoeken. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Alweer gelijk aan de 2D-versie. Hiernaast zie je twee vectoren waarvan de beginpunten in de oorsprong zijn gelegd (dat maakt voor de hoek natuurlijk niets uit). De cosinusregel in driehoek OPQ geeft: PQ2 = OP2 + OQ2 - 2OP • OQ • cosα Stel dat P = (a, b, c) en Q = (d, e, f ) dan geeft de cosinusregel: (d - a)2 + (e - b)2 + (f - c)2 = (a2 + b2 + c2) + (d2 + e2 + f 2) - 2OP • OQ • cosα |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Haakjes wegwerken en vereenvoudigen (al die kwadraten vallen weg): -2ad - 2be - 2cf = -2OP • OQ • cosα | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
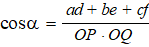| En die OP en OQ zijn weer de lengtes van beide vectoren. Dat in de teller is weer het inproduct. Mooi zo! Dat geeft precies dezelfde regel als bij 2D-vectoren. Ik hou van steeds dezelfde regels!! | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
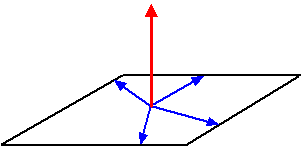
| 4. Normaalvector. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Kijk, nou komt er een
enorm verschil met 2D-vectoren! In drie dimensies heeft een vector niet meer EEN normaalvector. Je kunt er oneindig veel vinden die er loodrecht opstaan. Die rode vector hiernaast staat loodrecht op dat getekende vlak. Maar dan staat hij loodrecht op alle blauwe vectoren in dat vlak, en dat zijn er oneindig veel! Dus een 3D-vector heeft oneindig veel normaalvectoren. (die liggen dan trouwens wél altijd in één plat vlak) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Voor het vinden van een normaalvector kun je nog wel steeds de regel "inproduct = nul" gebruiken. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (Doe me een plezier: controleer even dat al die inproducten inderdaad nul worden). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
