© h.hofstede (h.hofstede@hogeland.nl)
De oppervlakte tussen grafieken
Twee grafieken
Hieronder staan een paar mogelijke liggingen van de grafieken waartussen je de oppervlakte wilt berekenen. In zulke gevallen bekijken we het steeds in etappes:

Stel dat de vraag is hoe groot de gele oppervlakte tussen de grafieken van f en g  is (in de linkerfiguur). 
In het midden hebben we de rode oppervlakte (onder de grafiek van f) uitgerekend. 
Maar nu hebben we duidelijk teveel. Wat moet er weer af?
Juist! De blauwe oppervlakte onder de grafiek van g rechts. 

In de volgende twee gevallen gebruiken we steeds dit principe. Daarbij moet je eraan denken dat bij een oppervlakte onder de x-as er een minteken voor de integraal moet staan.

En nou komt het opvallende: op de onderste regel van deze drie plaatjes (bij de integralen) staat steeds hetzelfde!!!
plaatje 1:   f - g
plaatje 2:  f + (-g)  en dat is ook  f - g
plaatje 3:  -g - (- f)  en dat is  -g + f  en jawel hoor!  Ook al  f - g
Conclusie:
Het is steeds "Bovenste - Onderste"

Tweede conclusie:

De plaats van de x-as doet er niet toe
1. a. De grafieken van f(x) = x2 - 5 en  g(x) = -2x - 2 sluiten samen een vlakdeel in (zie figuur linksonder).
Bereken algebraïsch de oppervlakte van dat vlakdeel.

102/3
b. De grafieken van  f(x) = 2√x - 2  en  g(x) = 4 - √x sluiten, samen met de y-as een vlakdeel in (zie figuur midden onder).
Bereken algebraïsch de oppervlakte van dat vlakdeel.

8
c. De grafieken  van f(x) = 6x2 - 2x - x3 - 4  en  g(x) = 2x2 - 14x - 4 sluiten samen twee vlakdelen in (zie figuur rechtsonder).
Bereken algebraïsch de oppervlakte van deze beide vlakdelen.

91/3 en 180

       
2.
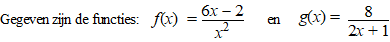  Bereken vervolgens algebraïsch de oppervlakte van het vlakdeel dat wordt ingesloten door de grafieken van f en g en de lijn x = 4. Geef je antwoord in twee decimalen nauwkeurig.
     

2,96
       
3. De Lorentzkromme.
De Lorentzkromme is een grafiek uit de economie Hij geeft de verdeling van inkomens van een bepaalde groep weer.  Zet alle mensen op volgorde van laag naar hoog inkomen. Op de x-as zet je nu hoeveel procent van de mensen je hebt gehad, en op de y-as hoeveel procent van het totaalinkomen die mensen hebben. 
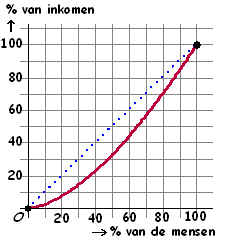
Hiernaast zie je een typische Lorentzcurve. Er is bijvoorbeeld in af te lezen dat  de 30% minst verdienende mensen samen slechts 15% van het inkomen verdienen.

De blauwe lijn hoort bij de meest gelijke inkomensverdeling: als iedereen precies evenveel verdient. De meest ongelijke verdeling zou je vinden als één persoon alles verdient, en dat zou de x-as van 0 tot 100 zijn plus een stip bij (100, 100)

Als getal om de inkomensongelijkheid van een groep weer te geven gebruiken economen de zogenaamde Gini-coëfficiënt.
Dat is de oppervlakte tussen beide grafieken gedeeld door de oppervlakte onder de blauwe lijn (en die is 5000).

Voor de Lorentzkromme van een land geldt ongeveer  f(x) = 0,02512x1,8
Bereken de Gini-coëfficient van dat land.
     

0,286
       
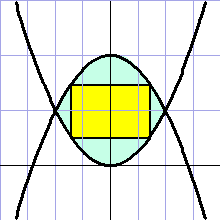
4. Tussen de twee parabolen
y = 0,25x2  en  y = 2 - 0,25x2  wordt een rechthoek getekend waarvan de hoekpunten op de parabolen liggen en waarvan de zijden evenwijdig aan de coördinaatassen zijn.

Hoeveel procent van de oppervlakte tussen beide parabolen wordt maximaal door de rechthoek in beslag genomen?

     

38,9%
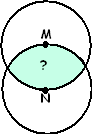
5. Twee cirkels met straal 3 doorsnijden elkaar zó dat het middelpunt van elke cirkel op de andere ligt. De vraag is: hoe groot is de doorsnede?

De vergelijking van een cirkel met middelpunt de oorsprong en straal 3 is
y2 + x2 = 9  ofwel  y = ±√(9 - x2).
Voor de bovenste helft van de cirkel geldt het plusteken, voor de onderste helft het minteken.

Kies als oorsprong punt N.  Dan is de cirkel met middelpunt M over afstand 3 omhoog geschoven.
       
a. Geef vergelijkingen voor de bovenste helft van de cirkel met middelpunt N en de onderste helft van de cirkel met middelpunt M.
     

y = √(9 - x2)
y = 3 - √(9 - x2)
b. Bereken de x-coördinaten van de snijpunten van beide cirkels.
     

±2,598
  c. Benader de oppervlakte tussen beide cirkels in twee decimalen nauwkeurig.
     

11,02
       
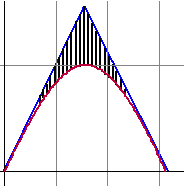
6. Hiernaast zie je een deel van de grafiek van
y = sinx met daarbij de raaklijnen
in x = 0 en x = π.
Bereken de exacte waarde van de oppervlakte van het gearceerde gebied.

     

0,25π2 - 2
       
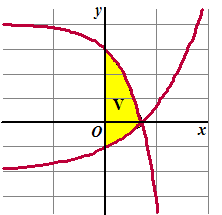
7. De grafieken van  y = ex - 2  en   y = 4 - e2x  en de y-as sluiten een vlakdeel V in.

Bereken algebraïsch de oppervlakte van V.

     

6ln2 - 2,5
       
8. Bereken de gezamenlijke oppervlakte van alle vlakdelen die worden ingesloten door de grafieken van y = 2x2 + 10 en y = 4x + 16 en x = -2 en x = 5
     

142/3
       
9. Examenvraagstuk VWO Wiskunde B, 2002

Gegeven is de functie:  f(x) = √(x - 1)

De lijn k raakt de grafiek van f in het punt P(10,3). Zie de figuur hieronder.
   
 

       
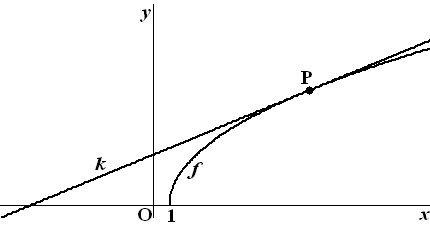  a. Stel met behulp van differentiëren een vergelijking op van k.
     

y = 1/6x + 11/3
  De grafiek van f, de lijn k en de x-as sluiten een vlakdeel in.
       
  b. Bereken exact de oppervlakte van dit vlakdeel.
     

32/3
       
Meer dan twee grafieken.
Stel dat we de oppervlakte van het gebied V tussen de drie grafieken hiernaast willen uitrekenen.
De grafieken horen bij de functies
f(x) = 8/x  en  g(x) = 4x  en  h(x) = x2

Dan kan dat niet in één keer met een oppervlakte tussen twee grafieken, omdat het gebied V niet steeds tussen dezelfde twee grafieken in ligt.
De oplossing is simpel:  Splits het gebied in stukken waarbij dat wél zo is!!!

Hieronder staat in een uitgebreid "stripverhaal"  hoe je dat een beetje systematisch kunt doen.

In het gebied V zijn verticale zwarte streepjes getekend.
In het linkerplaatje hierboven lopen die streepjes steeds van de blauwe naar de rode grafiek. De oppervlakte zal daar dus gelijk zijn aan de oppervlakte tussen de blauwe en de rode grafiek.
In het middelste plaatje is het grensgeval bereikt. Als we nu nog verder naar rechts gaan verandert de situatie, want dan gaan de streepjes tussen de blauwe en de groene grafiek lopen
In het rechterplaatje is dat het geval, dus is de oppervlakte gelijk aan de oppervlakte tussen de blauwe en de groene grafiek.
Als je berekent dat de snijpunten van de grafieken liggen bij x = √2 en x = 2 en x = 4  (doe dat zelf maar), dan geeft dat dus:

Uitrekenen is nog slechts een formaliteit, doe dat zelf maar (er komt trouwens 8 uit).
10. Gegeven zijn de functies:   f(x) = x2 - 4x  en  g(x) = -2x + 3  en  h(x) = x

De grafieken van deze drie functies sluiten samen drie vlakdelen in.
Bereken van ieder van die vlakdelen de oppervlakte. Doe dat algebraïsch.

131/6 en 71/2 en 131/3

 
11. De grafieken van y = 4x2 en  y = 7,5x + 1 en y = 1/2x sluiten een aantal vlakdelen in. 
Bereken algebraïsch de oppervlakte van vlakdeel V dat hiernaast is aangegeven.

 
   

63/20 + 1/2ln(2/5)
12. Examenvraagstuk VWO Wiskunde B, 2004

Gegeven zijn de functies:  f(x) = x2  en  g(x) = √x, beide met domein [0,→〉.
In de figuur hieronder zijn de grafieken van f  en  g  en ook de lijn y = 6 - x getekend.
Het gebied, ingesloten door de grafiek van f, de grafiek van g, en de lijn y = 6 - x, is in de figuur grijs gekleurd.
     
 

     
  Bereken algebraïsch de exacte oppervlakte van dit gebied.
   

32/3
     
 

© h.hofstede (h.hofstede@hogeland.nl)