| |
 |
| Verschuiven
van grafieken. |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
|
De grote vraag vandaag is "Wat
gebeurt er met de formule die bij een grafiek hoort, als je de grafiek
opzij of omhoog of omlaag verschuift?"
Daar hebben we meteen al 2 verschillende gevallen:
1. Omhoog of omlaag verschuiven.
2. Naar links of naar rechts verschuiven. |
 |
|
|
| Geval 1. Omhoog of
Omlaag verschuiven. |
|
|
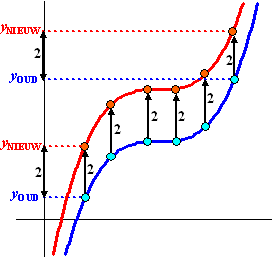
Laten we als voorbeeld een grafiek bekijken
die 2 omhoog wordt geschoven. Zie de figuur hiernaast.
De blauwe grafiek wordt 2 omhoog geschoven.
Dat betekent dat alle rode punten 2 hoger liggen dan hun blauwe
partners. Alle zwarte pijlen hebben dus lengte 2.
Op de y-as zie je bij twee zulke koppeltjes dat dan geldt dat yNIEUW ook
2 hoger ligt dan yOUD. Dus:
Maar de y is eigenlijk de uitkomst van de hele formule, dus
staat hier eigenlijk: NIEUWE
FORMULE = OUDE FORMULE +
2 |
 |
En wat voor 2 geldt, geldt natuurlijk voor elk
getal.
Conclusie: |
|
|
|
Grafiek a omhoog
schuiven ⇒ f(x)
wordt f(x) + a |
|
|
|
| En als de grafiek a
omláág wordt geschoven dan wordt dat natuurlijk f(x)
- a maar dat snapte je waarschijnlijk al wel. |
|
|
| Geval
2: Naar links of naar rechts schuiven. |
|
|
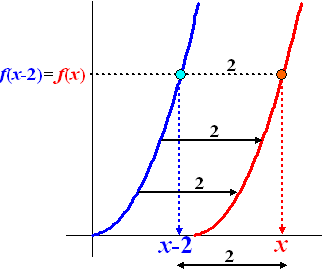
Laten we als voorbeeld een
grafiek bekijken die 2 naar rechts wordt geschoven. Zie de figuur
hiernaast. De blauwe grafiek gaat over in de rode.
Bekijk nu een punt van de nieuwe grafiek bij de rode x.
De y-waarde die daarbij hoort is dan fNIEUW(x).
Maar in de figuur zie je dat dat de y
van de blauwe grafiek is, die hoort bij x
- 2, dus dat is fOUD(x
- 2)
Conclusie: fNIEUW(x)
= fOUD(x
- 2)
In woorden: je krijgt het nieuwe functievoorschrift van de
verschoven grafiek door in het oude de x te vervangen door x
- 2.
En wat voor 2 geldt, geldt natuurlijk voor elk getal.
Je kunt het ook zo beredeneren:
|
| Als je x vervangt door (x-2), dan
moet je van de x die je wilt invullen eerst 2 aftrekken.
Dus om dezelfde y-waarde als bij de oorspronkelijke
grafiek te vinden, moet x dan juist 2 groter zijn. |
|
|
 |
| Conclusie: |
|
|
|
|
Grafiek a naar rechts
schuiven
⇒ x
vervangen door (x - a) |
|
|
|
• Het zal je niet verbazen
dat je de grafiek a naar links kunt schuiven door in de formule x
te vervangen door (x+ a).
• Als er meerdere x-en in de formule staan moet je ze allemaal
vervangen door (x ± a) |
| |
|
|
OPGAVEN |
|
|
|
|
|
|
| 1. Schets zonder de GR te
gebruiken de grafieken van de volgende functies: |
| |
|
|
|
|
|
a. |
y = (x - 3)2 |
e. |
f(x) = √(x
- 3) |
|
b. |
y = x2 - 4 |
f. |
y = 3 + √(x
+ 2) |
|
c. |
f(x) = 1/(x - 5) |
g. |
f(x) = 4 + 1/(x
+ 2) |
|
d. |
y = (x + 2)2 + 3 |
h. |
f(x) = (x + 1)3 |
|
|
|
|
| 2. |
Als je de lijn y = 2x
+ 4 over een afstand 3 naar rechts schuift krijg je
precies dezelfde grafiek als wanneer je hem 6 omlaag
schuift.
Toon dat aan! |
|
|
|
|
| 3. |
De top van een parabool is het punt
(3, 6). Geef een mogelijke vergelijking van zo'n parabool. |
|
|
|
|
| 4. |
a. |
De grafiek van y = x3
wordt zó verschoven dat hij door het punt (2, 1) gaat
Geef een mogelijke formule voor de grafiek die dan ontstaan is. |
| |
|
|
|
b. |
De grafiek van y = 1/x
wordt zo verschoven dat hij door (-1, 6) gaat.
Geef een mogelijke formule voor de grafiek die dan ontstaan is. |
| |
|
|
| |
c. |
De grafiek van y = √x
wordt 3 omhoog geschoven en daarna een afstand opzij.
Na afloop gaat de grafiek door (9, 8)
Hoeveel is de grafiek opzij geschoven, en welke kant op? |
| |
|
|
| 5. |
Examenvraagstuk HAVO
Wiskunde B, 2023-II
De
functie f wordt gegeven door f(x) =
x3 + 6x2
- 36x
- 88. Door de
grafiek van f twee naar rechts te verschuiven
ontstaat de grafiek van de functie g.
Een formule voor g is g(x) = x3
- 48x. |
| |
|
|
| |
a. |
Bewijs
dat dit een formule is voor g. |
| |
|
|
| |
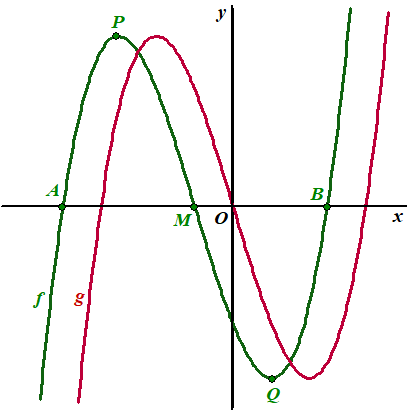
In de
volgende figuur zijn de grafieken van f en g
weergegeven. |
| |
|
|
| |
 |
| |
|
|
| |
Het
middelste snijpunt van de grafiek van g met de x-as
ligt in de oorsprong.
De grafiek van f heeft behalve punt M nog twee
snijpunten met de x-as: het punt A en het punt
B. De coördinaten van die snijpunten zijn met de
functie f moeilijk te berekenen. Met behulp van de
functie g zijn de coördinaten van deze snijpunten wel
te berekenen. |
| |
|
|
| |
b. |
Bereken
exact de x-coördinaten van A en B. |
| |
|
|
|
|
 |
|
|
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
|