| 1. |
Schets de grafieken van de volgende
functies en leg uit via welke transformaties (en in welke
volgorde) zij zijn ontstaan uit een basisgrafiek. |
| |
|
|
|
|
|
a. |
y = (x + 1)2
- 2 |
e. |
y = 5 - √(x
+ 3) |
|
b. |
f(x) = 3
- 2/x |
f. |
f(x) = (2x + 6)2 |
|
c. |
y = 4 - (2x)3 |
g. |
f(x) = 4 + 1/(x
+ 2) |
|
d. |
y = √(2x
- 4) |
h. |
f(x) = 2(4
- x)2
+ 1 |
|
|
|
|
|
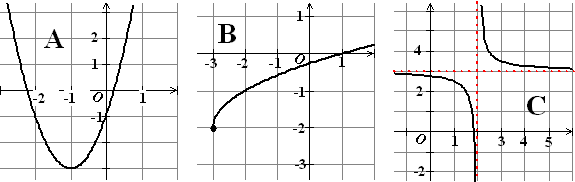
| 2. |
Geef een mogelijke formule voor
onderstaande grafieken. |
|
|
|
|
|
|
|
|
|
|
| 3. |
a. |
De grafiek van y
= 1/x wordt eerst 2 naar rechts geschoven, daarna
gespiegeld in de x-as en tenslotte wordt de afstand tot
de y as gehalveerd. Geef een functievoorschrift van de
grafiek die dan is ontstaan. |
| |
|
|
|
b. |
De grafiek van y = x2
wordt gespiegeld in de x-as. Daarna wordt hij 3 omhoog
geschoven en tenslotte wordt de afstand tot de y-as drie
keer zo groot gemaakt. Geef een functievoorschrift van de
grafiek die dan is ontstaan. |
| |
|
|
|
c. |
De grafiek van y =
√x
wordt 2 omlaag geschoven en 3 naar rechts. Daarna wordt de
afstand tot de x-as verdubbeld. Geef een
functievoorschrift van de grafiek die dan is ontstaan. |
| |
|
|
|
|
|
|
|
| 4. |
a. |
Als je de grafiek van y
= 3x afstand 2 naar links schuift krijg je
precies hetzelfde resultaat als wanneer je de afstand tot de x-as
9 keer zo groot maakt. Toon aan dat dat inderdaad zo is. |
| |
|
|
|
b. |
Je kunt de grafiek van y = x3
vermenigvuldigen en opzichte van de x-as met factor 8.
Je kunt de grafiek van y = x3 ook
vermenigvuldigen ten opzichte van de y-as met factor a.
Wat moet je voor a kiezen zodat het resultaat van deze
tweede vermenigvuldiging hetzelfde is als van de eerste? |
| |
|
|
|
|
|
|
|
| 5. |
Bekijk de volgende vier
transformaties: |
|
A:
B:
C:
D: |
4 naar rechts schuiven
afstand tot de y-as verdubbelen
3 omlaag schuiven
spiegelen in de x-as |
|
|
|
|
|
|
Van welk van deze transformaties doet
de volgorde er niet toe en van welke wél? |
|
|
|
|
| 6. |
Geef formules voor de
volgende grafieken: |
|
|
|
|
|
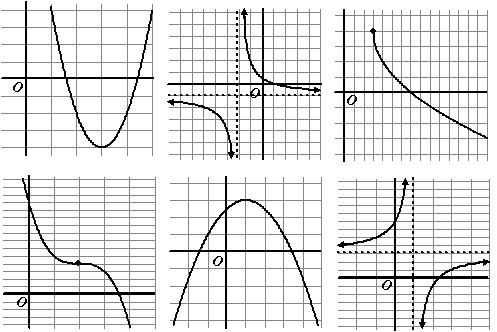
|
| |
|
|

|
| |
|
|
|
| 7. |
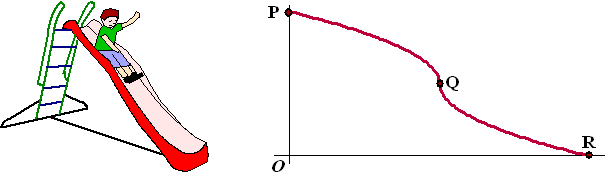
De
meeste glijbanen zijn nogal saai, zoals in de figuur linksonder.
Ik besluit een leukere glijbaan te ontwerpen….
Die staat in de figuur rechtsonder. Hij heeft in het midden bij
punt Q een spectaculaire
daling. Zoals je ziet is hij symmetrisch ten opzichte van punt
Q. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Als ik de oorsprong kies zoals in de figuur, dan voldoen de twee
delen van mijn glijbaan aan de volgende vergelijkingen: |
| |
PQ: y = 2 +
√(4 - 2x)
QR: y = 2 - √(2x
- 4) |
| |
|
|
|
| |
a. |
Bereken de hoogte van punt
Q. |
| |
|
|
|
| |
b. |
Leg uit hoe de grafiek van QR is ontstaan uit de grafiek van
y =
√x |
| |
|
|
|
| |
c. |
Leg uit hoe de grafiek van QR is ontstaan uit de grafiek van PQ. |
| |
|
|
|
| 8. |
examenvraagstuk HAVO
wiskunde B, 2016-I |
| |
|
|
|
| |
De functie f is gegeven
door f (x) = 3x
−1 − 2 . |
| |
|
|
|
| |
a. |
Schets de grafiek van f
en geef vergelijking(en) van de asympto(o)t(en) van deze
grafiek. |
| |
|
|
|
| |
De functie g is gegeven door g(x)
= 3x.
Op de grafiek van g worden de volgende
transformaties uitgevoerd: eerst de verschuiving 6 omlaag, gevolgd
door de vermenigvuldiging met 1/3
ten opzichte van de x-as. Op deze manier ontstaat de grafiek
van de functie h. |
| |
|
|
|
| |
b. |
Toon op algebraïsche wijze aan dat h
dezelfde functie is als f. |
| |
|
|
|
| |
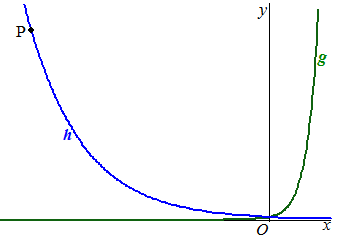
De grafiek van g wordt met a
vermenigvuldigd ten opzichte van de y-as.
Hierdoor ontstaat de grafiek van de functie k. Het punt P(−20,
81) ligt op de grafiek van k. Zie onderstaande figuur.
|
 |
| |
|
|
| |
c. |
Bereken exact
de waarde van a. |
| |
|
|
|
|
|
|
 |