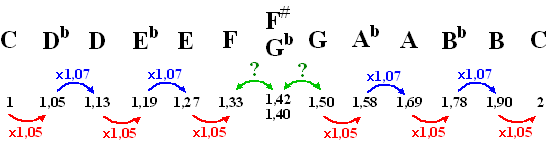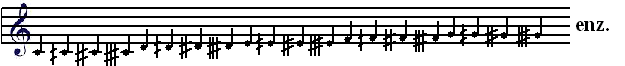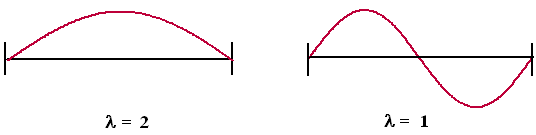
Toonsystemen.

© h.hofstede (h.hofstede@hogeland.nl)

       
Als je een snaar aanslaat, dan zal die op een bepaalde manier gaan trillen. De vorm van de snaar zal een staande golf in de vorm van een sinusgrafiek zijn, en omdat de uiteinden vastzitten weet je dat daar de nulpunten van die grafiek moeten zitten. Maar dat geeft nog steeds meerdere mogelijke grafieken. Hieronder zie je de eenvoudigste twee:
       

       
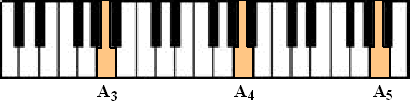
Eerst even een paar termen:   De golflengte (l) is de breedte van zo'n sinusgrafiek. De frequentie (f) is het aantal trillingen per seconde en is omgekeerd evenredig aan de golflengte. 

Als je de lengte van de snaar 1 noemt, dan heeft de eerste een golflengte van l = 2 en de tweede een golflengte van l  = 1
Maar de golflengte is omgekeerd evenredig aan de frequentie (f ) van de toon.  Dus als de golflengte van de tweede toon de helft is van de eerste, dan is de frequentie het dubbele.
Dus als je een toon van een bepaalde frequentie hebt, dan is de meest natuurlijke die daarbij hoort de toon met dubbele frequentie (of met halve frequentie). Die tonen hebben we daarom dezelfde naam gegeven. De afstand ertussen noemen we een "octaaf"  (omdat we deze afstand straks in 8 stukjes gaan verdelen).

Laten we bijvoorbeeld de toon A nemen. De laagste A-toon die onze muziek kent noemen we A0 en die heeft een frequentie van  27,5 Hz.  Dat betekent dat de eerstvolgende A een frequentie heeft van A1 = 2 • 27,5 = 55 Hz. En daarop volgen dan A2 = 110 Hz, A3 = 220 Hz,  A4 = 440 Hz, A5 = 880 Hz enz.
       

       
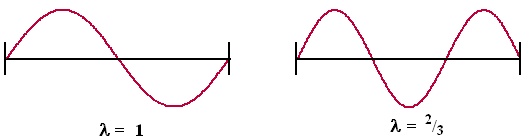
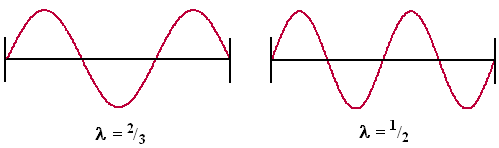
Laten we de volgende stap nemen. De volgende meest simpele sinusgrafiek die op zo'n snaar past zie je hier:
       

       
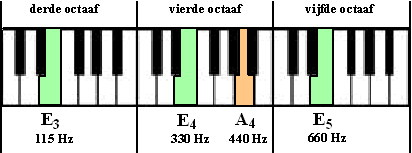
De golflengte wordt 2/3 en dat betekent dat de frequentie 1,5 keer zo groot wordt. Dus als we hebben A4 = 440 Hz is de volgende interessante toon de toon met 440 • 1,5 = 660 Hz. Die volgende toon heet E5, en de afstand tussen A4 en E5 noemen we een kwint. En vanaf  E5 kun je door verdubbelen-halveren natuurlijk ook makkelijk E4, E6, E3, E2 enz vinden.
       

       
Die volgende E  na A4 heet E5 en niet E4 omdat we tussen de tonen C tellen. Zoals je hierboven ziet ligt de E met frequentie 660 Hz in het volgende octaaf, daarom noemen we hem E5. Maar door de E5 door 2 te delen krijgen we toch een E-toon (namelijk E4) in het vierde octaaf.

Volgende stap bij de snaar:
       

       
Hier gaat de golflengte van 2/3 naar 1/2  dus de frequentie van 3/2 naar 2  Dat is een vermenigvuldiging met 4/3.
Maar omdat verdubbelen dezelfde toon geeft, kunnen we onze "nieuwe" toon ook vinden door te vermenigvuldigen met 2/3.

Maar kijk! Dat is hetzelfde als delen door 3/2.  Oftewel: het is de kwint de "andere kant op" (omlaag in plaats van omhoog). Die heet in onze muziektheorie een "kwart".  

Pythagoras vond dit het mooiste wat er maar kon gebeuren.  Hij was nogal gek op gehele getallen en de verhoudingen daartussen. En kijk wat er hier gebeurt:

•  De verhouding tussen een toon en zijn octaaf is  1 : 2
•  De verhouding tussen een toon en zijn kwint is   2 : 3
•  De verhouding tussen een toon en zijn kwart is   3 : 4. 

Mooier kan eigenlijk niet!!!
('t is natuurlijk eigenlijk niets anders dan de verhouding van de golflengtes van die sinusgrafiekjes hierboven)

Laten we daarom vanaf een centrale toon (de C4)  kwinten omhoog  gaan maken.
Stel de frequentie van die C4 voorlopig gelijk aan 1.
Dat geeft de volgende stijgende kwinten (steeds ´1,5).
       

       
Als je alle tonen binnen het vierde octaaf (tussen C4 en C5) wilt terugbrengen dan moet je die D5 en A5 dus door twee delen, en die E6 en B6 door 4 en die F#7 zelfs door 8.  Dat geeft:
G4 =  3/2 ≈ 1,5000
D4  =  1/2 • (3/2)2 =   9/8 ≈ 1,1250
A4  =  1/2 • (3/2)3 =  27/16 ≈ 1,6875
E4  =   1/4 • (3/2)4 =   81/64 ≈ 1,2656
B4  =  1/4 • (3/2)5  = 243/128 ≈ 1,8984
F#4 =  1/8 • (3/2)6 = 729/512  ≈ 1,4238
       
Laten we ook zes stappen omlaag gaan.  Dat geeft de volgende dalende kwintenlijn (steeds ×2/3). Je moet hem dus van rechts naar links lezen.
       

       
En weer terugbrengen tot het octaaf tussen C4 en C5:
       
F4  =   2 • 2/3 ≈ 1,3333
Bb4  =  4 • (2/3)2 =   16/9 ≈ 1,7778
Eb4  =  4 • (2/3)3 =  32/27 ≈ 1,1852
Ab4  =  8 • (2/3)4 =   128/81 ≈ 1,5802
Db4  =  8 • (2/3)5  = 256/243 ≈ 1,0535
Gb4 =  16 • (2/3)6 = 1024/729  ≈ 1,4047
       
Zetten we alle tot nu toe gevonden tonen op volgorde vanaf C, dan geeft dat:
       

       
De factoren zijn regelmatig om en om ongeveer 1,05 (exact 256/243) en 1,07 (exact 2187/2048)
Maar daar in het midden past het niet aan elkaar! Die F# en die Gb zitten ongeveer op dezelfde plaats, maar niet precies.
Als je van F naar G gaat kun je eerst met 1,05 vermenigvuldigen en dan met 1,07, dat geeft Gb.
Als je van F naar G gaat kun je ook eerst met 1,07 vermenigvuldigen en daarna met 1,05, dat geeft F#.
Die twee groene pijlen leveren samen een rode en een blauwe op, maar in welke volgorde?

Dit kleine verschuil tussen F# en Gb (van ongeveer 0,02) heet het "Pythagoreïsch komma".
Twaalf kwinten verschil geeft bij Pythagoras een factor  (3/2)12 = 129,7463379
Dat zou hetzelfde zijn als 7 octaven:  27  = 128. En dat is dus niet zo. Het scheelt een  factor  (1.5)12 /27 = 1,013643265  
 
Als je wilt vasthouden aan die "mooie" verhoudingen van de Pythagoreërs, dan zijn F# en Gb niet dezelfde toon. Maar als je vanaf F# nog een kwint hoger gaat krijg je C#  en dat is dan ook niet dezelfde toon als een kwint omhoog vanaf  vanaf Gb (dat is Db). En zo gaat dat alsmaar door!

Gelijkzwevende Stemming. (equi-tempered scale)

In deze stemming wordt elke kwint verlaagd met 1/12 van het Pythagoreïsch komma. Die 1,0136... verschil wordt als het ware uitgesmeerd over alle kwinten. Dat zorgt ervoor dat, als je 6 kwinten omhoog gaat, en ook zes omlaag (12 kwinten) dat dan die Gb en F#  wél precies passen. Twaalf kwinten geeft nu wél precies zeven octaven.
In dit geval geldt dus voor de vermenigvuldigfactoren  g12 = 2  ofwel  g = 21/12 = 1,059463094.

Tegenwoordig is het gebruikelijk om uit te gaan van een A4 = 440Hz.
Dat geeft met de gelijkzwevende stemming de volgende frequenties:
       
C C#/Db D D#/Eb E F F#/Gb G G#/Ab A A#/Bb B C
261,63 277,18 293,66 311,13 329,63 349,23 369,99 391,99 415,30 440 466,16 493,88 523,25
       
Zoals je ziet is C5 = 523,25 nu precies het dubbele van C4 = 261,63.
Vergelijk met de "Zuivere"stemming van Pythagoras:
       
  C Db D Eb E F F#/Gb G Ab A Bb B C
gelijkzwevend 261,63 277,18 293,66 311,13 329,63 349,23 369,99 391,99 415,30 440 466,16 493,88 523,25
zuiver 260,74 274,69 293,33 309,03 330 347,65 371,25
366,25		 391,11 412,03 440 463,54 495 521,48
       
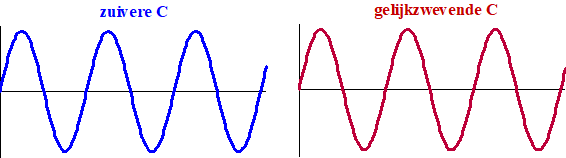
Hier is een geluidsfragment waarin je het verschil tussen de zuivere stemming en de gelijkzwevende stemming kunt horen.

Voor de meer visueel ingestelde "luisteraars (?)".

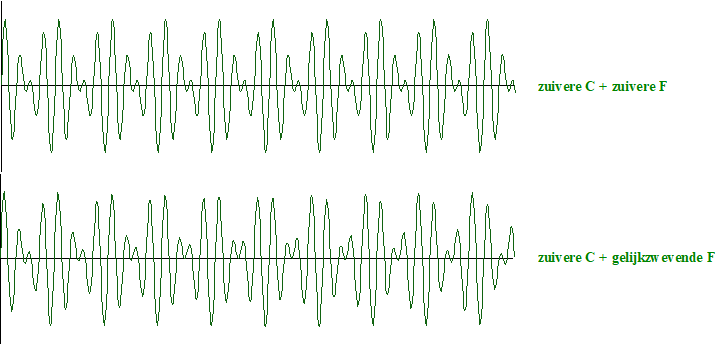
Hieronder zie je de snaar met een zuivere C en met een gelijkzwevende C. Je ziet er eigenlijk geen verschil tussen. Zelfs als je ze op elkaar zou leggen dan zien nog maar één golf; het verschil is kleiner dan de dikte van de tekenlijn.
       

       
En voor de zuivere F en de gelijkzwevende F geldt precies hetzelfde.

Maar kijk wat er gebeurt als je een zuivere C met een zuivere F samenneemt, OF als je een zuivere C met een gelijkzwevende F samenneemt:
       

       
De oplettende kijker ziet nu wel verschillen (net zoals de oplettende luisteraar verschillen kan horen).
       
           
   OPGAVEN
           
1. De kwarttoonverdeling verdeelt een octaaf (ook gelijkzwevend) in 24 verschillende tonen, waarvoor de volgende notatie is verzonnen (ook met mollen in plaats van kruizen is er trouwens zo'n soort notatie):
 

   
  a. Bereken de frequentie van de tonen tussen de A en de B, waarbij de A weer 440Hz is.
     
  b. Christiaan Huygens ontwikkelde een 31-toonssysteem (gelijkzwevend).
Welke tonen uit zijn systeem zullen het dichtst bij "onze" tonen liggen?
     
   
2. Praktische Opdracht.

Ga eens op zoek naar een aantal andere toonsystemen, en leg de werking en de verschillen daartussen duidelijk uit.
Dit zijn mogelijke trefwoorden:
•  Bohlen-Pierce-schaal.
•  Middentoonsstemming.
•  Werckmeister.
           
       

© h.hofstede (h.hofstede@hogeland.nl)