| |
 |
| Tekenbeeld. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
Bij het bepalen van de extremen van een functie hebben we gevonden:
|
| Bij een maximum of
minimum van f geldt f '
= 0 |
|
|
|
|
|
| Maar ehmm.... Hoe weet je nou of 't
een maximum of een minimum is ?
Daar kun je op twee manieren achter komen.
De simpelste manier is om de grafiek te plotten en gewoon te kijken of er
een top of een dal zit bij de x die je hebt berekend. De tweede (en
iets nettere) manier is om een zogenaamd tekenbeeld van de
afgeleide functie te maken. Dat gaat als volgt:
|
|
| • |
Teken een getallenlijn met de x-en waar
de functie en de afgeleide bestaan (let op het domein). Zet kruisjes bij
eventuele x-waarden waar f of f '
niet bestaan. |
| • |
Zet stippen met een 0 erboven bij de x-waarden
waar de afgeleide nul was (die heb je net uitgerekend). |
| • |
Zet plustekens boven de lijn op de plaatsen
waar de afgeleide positief is, mintekens waar hij negatief is. Of de
afgeleide positief of negatief is bij een deel van de lijn kun je
ontdekken door gewoon een x te proberen (invullen in de
afgeleide) |
|
|
Voorbeeld:
Gegeven is de functie f(x) = 2x3 +
3x2 - 36x
De afgeleide is f '(x) = 6x2 +
6x - 36
Dat is nul als x = 2 of x = -3 (doe maar
met de ABC-formule of ga ontbinden)
Het domein van de functie is "alles". Teken daarom een lijn
met stippen met een nul erboven bij x = 2 en x = -3.
Links van x = -3 zit bijvoorbeeld x = -4, en als je
dat invult in de afgeleide komt eruit f '(-4) = 36 en dat
is positief dus daar zetten we plustekens neer.
Tussen x = -3 en x = 2 zit bijvoorbeeld x = 0, en
omdat f '(0) = -36 zetten we daar mintekens neer.
Rechts van x = 2 zit bijvoorbeeld x = 3, en omdat f '(3)
= 36 zetten we daar plustekens neer.
Dat geeft het volgende tekenbeeld van de afgeleide: |
|
|
|

|
|
|
Omdat rechts van x = 3
plustekens staan is de afgeleide daar positief, dus de functie zelf
stijgend. Rechts van -3 is de afgeleide negatief dus de functie zelf
dalend. Dus bij x = -3 gaat de functie over van stijgend naar
dalend.
Dat kan alleen als bij x = 3 een maximum zit!!!
Op dezelfde manier kun je beredeneren dat de functie bij x = 2
een minimum zal hebben. |
|
|
Nog een voorbeeld
Gegeven is de functie f(x) = x√x
- 6x
Dat is gelijk aan f(x) = x1,5
- 6x dus de afgeleide is f '(x) = 1,5
• x0,5 - 6 en dat is 1,5√x
- 6
1,5√x - 6 = 0 ⇒
√x = 4 ⇒
x = 16.
f(x) bestaat alleen voor x ≥
0.
f '(1) = -4,5 dus daar staan mintekens. f '(25) =
1,5 dus daar staan plustekens.
Dat geeft het volgende tekenbeeld van de afgeleide: |
|
|
|
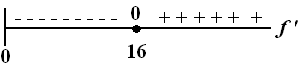
|
|
|
| Bij x = 16 gaat de functie
van dalend naar stijgend, dus daar zal een minimum zitten. |
|
|
Nou, nog ééntje dan...
Gegeven is de functie f(x) = 3x
+ 12/x
Dat is gelijk aan f(x) = 3x + 12x -1
dus de afgeleide is gelijk aan f '(x) = 3 - 12x
-2 = 3 - 12/x²
3 - 12/x² = 0 ⇒
12/x² = 3 ⇒
x2 = 4 ⇒ x
= 2 ∨ x = -2
f(x) bestaat overal, behalve bij x = 0.
f '(-3) = 12/3 dus daar staan plustekens.
f '(-1) = -9 dus daar staan mintekens.
f '(1) = -9 dus daar staan mintekens.
f '(3) = 12/3 dus daar staan plustekens.
Dat geeft het volgende tekenbeeld voor de afgeleide: |
|
|
|
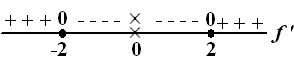
|
|
|
De conclusie is dat deze functie
bij x = -2 een maximum heeft en bij x = 2 een minimum.
Speciaal geval.
Bij de volgende functie gebeurt er iets raars.
Kijk maar.
Neem f(x) = x3 - 9x2 +
27x
De afgeleide is f ´(x) = 3x2
- 18x + 27
3x2 - 18x + 27 = 0 ⇒
x2 - 6x + 9 = 0 ⇒
(x - 3)(x - 3) = 0 ⇒
x = 3.
f '(2) = 3 dus daar staan plustekens, en f '(4) = 3 dus
daar staan ook plustekens.
Dit is het tekenbeeld van f ' :
|
|
|
|
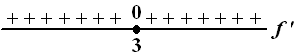
|
|
|
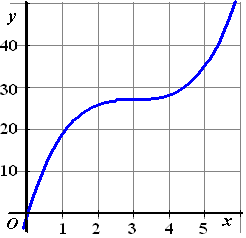
Links van x = 3 stijgt de
grafiek en rechts van x = 3 ook. Alleen bij x = 3
zélf is de raaklijn horizontaal. De grafiek staat
hiernaast geschetst.
We hebben hier dus een geval waarbij wél geldt dat f
' = 0 maar waarbij er toch geen maximum of minimum is.
Kortom; de regel bovenaan dit hoofdstuk mag je niet zomaar
omdraaien: als er een maximum of minimum is, dan is de afgeleide
nul, maar als de afgeleide nul is, dan hoeft er nog geen
maximum of minimum te zijn. |
|
|
| |
|
| En
f zélf; kun je daar ook een tekenbeeld van maken? |
| |
|
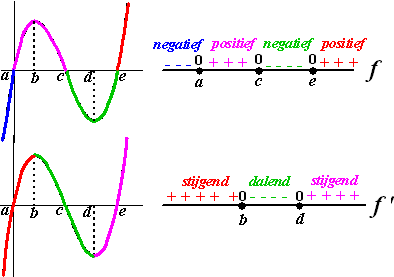
| Natuurlijk. Bedenk je alleen wél dat een
tekenbeeld zegt of de formule een positief of negatief antwoord geeft.
Een tekenbeeld van f zelf zegt daarom of de y positief of
negatief is, dat wil zeggen of de grafiek boven of onder de x-as
zit. De punten waar f = 0 zijn de snijpunten met de x -as
(de nulpunten). Hieronder zie je een grafiek met het
tekenbeeld van f en ook dat van f ' dat bij die grafiek
hoort. |
| |
|
| |
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
Geef de extremen van onderstaande
functies. Laat steeds met een tekenbeeld zien of er sprake is
van een maximum of minimum of geen van beiden. |
|
| |
|
| a. |
f(x) = 2x3
- 15x2 + 24x - 8 |
| |
|
| b. |
f(x) = 32/x²
- 12 + 2x2 |
| |
|
| c. |
f(x) = x2 •
(√x - 4) |
|
| |
|
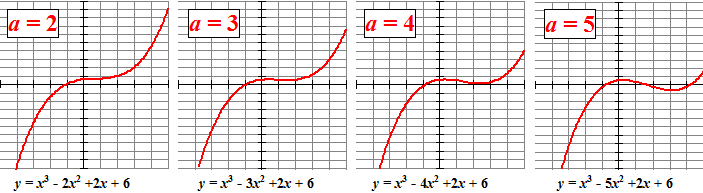
| 2. |
Hieronder staat een serie grafieken bij functies
van de vorm y = x3 - ax2
+ 2x + 6 |
| |
|
|
|
|
|
| |
|
|
|
| |
Bij grote a (4 en 5) lijkt de
grafiek een maximum en een minimum te hebben. Bij a = 2
lijkt de grafiek constant te stijgen. Bij a = 3 is het
een beetje slecht te zien......
Bereken algebraïsch voor welke waarden van a de grafiek
van deze functie een maximum en een minimum heeft. |
| |
|
|
|
| 3. |
Hieronder zie je vier keer onder
elkaar een tekenbeeld van f en ook van f '.
Schets een mogelijke grafiek die bij deze tekenbeelden zou
kunnen horen. |
| |
|
|
|
| |
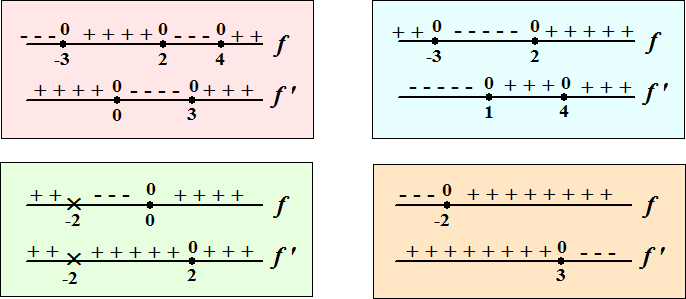
|
| |
|
|
|
| 4. |
Er zijn zelfs functies waarbij in
het tekenbeeld f wel bestaat, maar f '
niet!!!
Vreemd toch: er is wel een grafiek maar hij heeft geen
helling!!!??? |
| |
|
|
| |
a. |
Denk daar eens minstens 10 minuten
over na en probeer zo'n functie/grafiek te verzinnen. |
| |
|
|
| |
b. |
Schets de grafiek van y =
x1/3 . |
| |
|
|
| |
c. |
Bereken de afgeleide van x1/3
en schets de grafiek van deze afgeleide. |
| |
|
|
| |
d. |
Kun je in het algemeen zeggen voor
welke functies xn de functie zelf wel ergens
bestaat maar de afgeleide niet? |
| |
|
|
|
| 5. |
Gegeven zijn de functies fp(x)
= 1/3x3 + px2
|
| |
|
|
|
|
a. |
Bereken algebraïsch de coördinaten
van de punten op de grafiek van f1 waar de
richtingscoëfficiënt van de raaklijn aan deze grafiek gelijk
is aan 3. |
| |
|
|
|
b. |
Voor welke p heeft fp
een extreme waarde 36? Onderzoek of dit een maximum of
een minimum is. |
|
|
|
|
| |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|