|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Voor de tangens van een hoek
α geldt tanα
= sinα/cosα Dat volgt bijvoorbeeld direct al uit sos-cas-toa: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
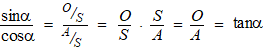| Dat tangens een breuk is heeft
belangrijke gevolgen voor de grafiek van y = tanx. Immers
als de noemer van een breuk nul is, dan bestaat die breuk niet, en dat
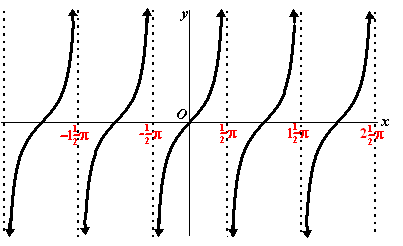
geeft in de grafiek een verticale asymptoot. Dus op de plaatsen waar cosx = 0 zal de grafiek van tanx een asymptoot hebben. Dat is bij x = 1/2π en x = 11/2π (en natuurlijk dan ook 21/2π, 31/2π, enz.). De tangensgrafiek ziet er daarom uit als hieronder: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Je ziet dat de periode van deze grafiek niet 2π is zoals bij sinx en cosx, maar π. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vergelijkingen met tangens. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dat periodiek zijn van de grafiek
heeft gevolgen voor het oplossen van vergelijkingen. Als je moet oplossen tanx = a dan kun je één oplossing natuurlijk makkelijk vinden met x = tan-1a, net zoals bij sinus en bij cosinus. Maar omdat de periode van de tangensgrafiek gelijk is aan π, zijn alle waarden x = tan-1a + kπ óók oplossingen. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Voorbeeld. Los op in [0, 2π]: 2 + 4tan(2x + 1) = 10. Geef je antwoord in twee decimalen. 2 + 4tan(2x + 1) = 10 ⇒ 4tan(2x + 1) = 8 ⇒ tan(2x + 1) = 2 ⇒ 2x + 1 = 1,11 + k • π (hier is dus tan-1(2) gebruikt om die 1,11 te vinden) ⇒ 2x = 0,11 + k • π ⇒ x = 0,55 + k • 0,5π Dat geeft in interval [0, 2π] vier oplossingen: 0,55 en 2,12 en 3,70 en 5,27. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| OPGAVEN | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6.
