© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. 5 - 2tan(1 - x) = 8
-2tan(1 - x) = 3
tan(1 - x) = -1,5
1 - x = -0,98 + kπ
-x = -1,98 + kπ
x = 1,98 + kπ
In interval [0, 2π] geeft dat de oplossingen  {1.98, 5.12}
       
  b. 2 + tan(2x + 8) = 12
tan(2x + 8) = 10
2x + 8 = 1,47 + kπ
2x = -6,53 + kπ
x = -3,26 + k • 1/2π
In interval [0, 2π] geeft dat de oplossingen {1.45, 3.02, 4.59, 6.66}
       
  c. 4tan2x  - 16 = 0
4tan2x = 16
tan2x = 4
tanx = 2  ∨   tanx = -2
x = 1,11 + kπ  ∨  x = -1,11 + kπ
In interval [0, 2π] geeft dat de oplossingen  {1.11, 2.03, 4.25, 5.18}
       
  d. 3tan(0,5x) =  5 - tan(0,5x)
4tan(0,5x) = 5
tan(0,5x) = 1,25
0,5x = 0,90 + kπ
x = 1,79 + k4π
In interval [0, 2π] geeft dat de oplossing  {1.79}
       
2. a. 2tan2x + 1 = 7
2tan2x  = 6
tan2x = 3
tanx = √3  ∨   tanx = -√3
x = 1/3π + kπ  ∨   x = -1/3π + kπ
In interval [0, 2π] geeft dat de oplossingen  {1/3π, 2/3π,  11/3π, 12/3π} 
       
  b. tan2x - tanx = 0
tanx(tanx - 1) = 0
tanx = 0  ∨  tanx = 1
x = 0 + kπ  ∨  x = 1/4π + kπ
In interval [0, 2π] geeft dat de oplossingen {0, 1/4π, π, 11/4π}
       
  c. 2tan(x- 1/2π) = 2/3√3
tan(x - 1/2π) = 1/3√3
x - 1/2π = 1/6π + kπ
x = 2/3π + kπ
In interval [0, 2π] geeft dat de oplossingen {2/3π, 12/3π}
       
  d. tan(2x + π) = tan(1/3π + x)
2x + π = 1/3π + x + kπ
x = -2/3π + kπ
In interval [0, 2π] geeft dat de oplossingen {1/3π, 11/3π}
       
3. a. tanx = 2sinx
sinx/cosx = 2sinx
sinx = 2sinxcosx
sinx - 2sinxcosx = 0
sinx(1 - 2cosx) = 0
sinx = 0   cosx = 1/2
x = 0 + k2π  ∨   x = π - 0 + k2π  ∨   x = 1/3π + k2π  ∨   x = 2π - 1/3π + k2π
In interval [0, 2π] geeft dat de oplossingen {0, 1/3π, π,  12/3π, 2π}
       
  b. tanx • sinx = cosx
sinx/cosx • sinx = cosx
sin2x = cos2x
sinx = cosx  Ú  sinx = -cosx
sinx = sin(1/2π - x)   ∨  sinx = sin(-1/2π + x)
x = 11/2π - x + k2π  ∨  x = π - (1/2π - x) + k2π  ∨  x = -1/2π + x + k2π  ∨  x =  π - (-1/2π + x) + k2π   
2x = 1/2π + k2π ∨  0 = 1/2π + k2π  ∨  0 = -1/2π + k2π  ∨  2x = 11/2π + k2π
x = 1/4π + kπ  ∨  x = 3/4π + kπ
In interval [0, 2π] geeft dat de oplossingen  {1/4π, 3/4π, 11/4π, 13/4π}
       
  c. 3tanx + 2cosx = 0
3 • sinx/cosx + 2cosx = 0
3sinx + 2cos2x = 0
3sinx + 2(1 - sin2x) = 0
3sinx + 2 - 2sin2x =  0    noem  sinx = p
-2p2 + 3p + 2 = 0
ABC-formule:  p = (-3 ±√(9 + 16))/-4 = (-3 ± 5)/-4  =  2  of  -1/2
sinx = 2 kan niet, dus blijft over sinx = -1/2
x =11/6π + k2π  ∨   x = π - 11/6π + k2π
In interval [0, 2π] geeft dat de oplossingen  {11/6π,15/6π}
       
  d. tanx = 2/3sin2x
sinx/cosx = 2/3sinxcosx
sinx = 2/3sinxcos2x 
sinx = 2/3sinx(1 - sin2x)
sinx = 2/3sinx - 2/3sin3x   noem nu  sinx = p
1/3p + 2/3p3 = 0
1/3p(1 + 2p2) = 0
p = 0 ∨  p2 = -1/2
p = 0
sinx = 0 
x = 0 + k2π ∨ x = π + k2π
In interval [0, 2π] geeft dat de oplossingen  {0, π, 2π}
       
  e. tanx = 3sinx - sin2x
sinx/cosx = 3sinx - 2sinxcosx
sinx = 3sinxcosx - 2sinxcos2x
sinx - 3sinxcosx - 2sinxcos2x = 0
sinx(1 - 3cosx - 2cos2x) = 0
sinx = 0  ∨  1 - 3cosx - 2cos2x = 0  noem in deze laatste vergelijking  cosx = p
sinx = 0  ∨   -2p2 - 3p + 1 = 0
sinx = 0  ∨  p = (3 ±√(9 + 8))/-4  =  -1,78  of  0,28
sinx = 0  ∨  cosx = 0,28
x = 0  + k2π ∨  x = π + k2π ∨  x = cos-1(0,28) = 1,29   ∨   x = 2π - 1,29 = 5,00
In interval [0, 2π] geeft dat de oplossingen  {0, 1.29,  π,  5.00, 2π}
       
  f. 1/2sin2x = √3cos2x
 1/2 • 2sinxcosx = √3•cos2x
sinxcosx = √3cos2x
sinxcosx - √3cos2x = 0
cosx (sinx - √3cosx) = 0
cosx = 0 ∨  sinx = √3cosx
cosx = 0  ∨  sinx/cosx = √3
cosx = 0  ∨  tanx = √3
x = 1/2π ∨  x =11/2π  ∨  x = 1/3π  ∨  x = 11/3π  
       
4.
       
5. sinx/cosx = 3  dus  sinx = 3cosx
maar ook is  sin2x + cos2x = 1
(3cosx)2 + cos2x = 1
10cos2x = 1
cos2x = 0,1
cosx = √0,1   (positief omdat x tussen 0 en 1/2π ligt)
sinx = 3cosx = 3√0,1
sin2x = 2sinxcosx = 2 • √0,1 • 3√0,1 = 6 • 0,1 = 0,6 
       
6. Er zijn oplossingen als  tegelijk geldt:  tanx - asin2x = 0  en   sinx ≠ 0
tanx = asin2x
sinx/cosx = 2asinxcosx
sinx = 2asinxcos2x
sinx = 2asinx(1 - sin2x)
sinx = 2asinx - 2sin3x
0 = sinx(2a - 1)  - 2sin3x
0 = sinx(2a - 1 - 2sin2x)
sinx =  0  ∨  2a - 1 - sin2x = 0
sinx = 0  ∨  sin2x = 2a - 1
De oplossingen aan de linkerkant voldoen niet want sinx ≠ 0
De rechterkant heeft geen oplossing als  2a - 1 > 1  of als 2a - 1 < 0  want sinx zit altijd tussen -1 en 1 dus sin2x zit tussen 0 en 1.
dat is zo als  a > 1 of als  a < 1/2.
       
7. tan(90º - x) = sin(90º - x)/cos(90º - x) = cosx/sinx = 1/tanx

tan1° • tan2° • tan3° • ... • tan89° 
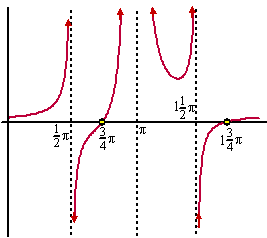
= (tan 1º • tan 89º) • (tan2º • tan88º) • (tan3º • tan87º) • .... • (tan44º • tan46º) • tan45º
Elke factor hierin is 1, dus als je ze allemaal met elkaar vermenigvuldigt komt er nog steeds 1 uit.
       
8. (1 + tanx)/(1 + cosx) = 0
1 + tanx = 0   (en 1 + cosx ¹ 0)
tanx = -1  (en x ¹ π)
x = 3/4π  ∨   x = 13/4π
Hiernaast staat de grafiek van  y = (1 + tanx)/(1 + cosx)

Dat is groter of gelijk aan  nul voor;
[0, 1/2π〉  en  [3/4π, π〉  en  〈π, 11/2π〉 en   [13/4π, 2π]
       
9. sin2x = 2sinxcosx  dus  sinx = 2sin1/2xcos1/2x
cos2x = 2cos2x - 1  dus   cosx = 2cos2(1/2x) - 1
Dat gaan we hier gebruiken:
 
       
10.
       
11.
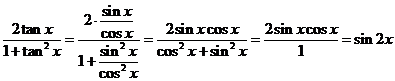  daarbij is in de tweede stap alles vermenigvuldigd met cos2x
       

© h.hofstede (h.hofstede@hogeland.nl)