|
|
 |
|
Stochasten optellen. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
Deze les gaan we kijken wat er
gebeurt als je meerdere dingen die van kansen afhangen (stochasten) bij
elkaar optelt.
Laten we beginnen twee volomen verschillende dingen bij elkaar op te
tellen.
Zomaar als experiment. |
| |
|
Stel dat ik uit de vaas hiernaast willekeurig
4 knikkers pak, en tel hoeveel roden erbij zijn. Daarna draai ik de
schijf, en tel het getal dat de schijf oplevert bij dat aantal rode
knikkers op. Dan krijg ik een nieuw getal.
Hoe zit het met dat nieuwe getal?
Wat is het gemiddelde?
Wat is de standaarddeviatie? |
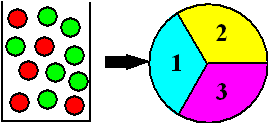 |
| |
|
Eerst maar eens apart
uitrekenen.....
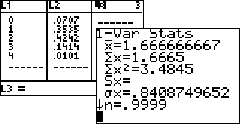
Voor het aantal rode knikkers geldt de volgende kansverdeling (je had
uiteraard het vaasmodel herkend toch?) |
| |
|
| aantal rood |
0 |
1 |
2 |
3 |
4 |
| kans |
0,0707 |
0,3535 |
0,4242 |
0,1414 |
0,0101 |
|
 |
| |
| Rechts zie je dat geldt E = 12/3
en
σ = 0,841 |
| Precies hetzelfde voor de schijf is nog
eenvoudiger: |
|
| |
|
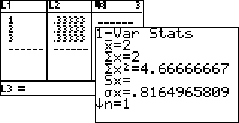
| cijfer van de schijf |
1 |
2 |
3 |
| kans |
1/3 |
1/3 |
1/3 |
|
 |
| |
| Rechts zie je dat geldt E = 2 en
σ = 0,816 |
| |
|
En daarna bij elkaar opgeteld....
Als je het aantal rode ballen optelt bij het getal van de schijf, dan
variëren de mogelijke uitkomsten nu van 1 (nul rode en schijf 1)
en tot en met 7 (4 roden en schijf 3).
Dat geeft de volgende kansverdeling: |
| |
|
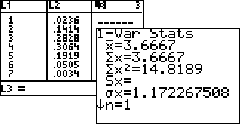
| som |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| kans |
0,0236 |
0,1414 |
0,2828 |
0,3064 |
0,1919 |
0,0505 |
0,0034 |
|
 |
| |
| Rechts zie je dat geldt E = 32/3
en
σ = 1,172 |
| |
|
Wat hebben die getallen met elkaar
te maken?
Nog even samengevat:
We vonden E1 = 12/3
en E2 = 2 en Esom = 32/3
En we vonden
σ1 = 0,841 en
σ2 = 0,816 en
σsom
= 1,172
Ik denk dat je het verband tussen die E's wel ziet: Esom
is gewoon die andere beide E's bij elkaar opgeteld.
Maar hoe zit het met de standaarddeviaties?
Wat is het verband tussen
0,841 en 0,816 en 1,172 ???
Dat is lastig te zien.
Totdat je je realiseert dat de standaarddeviatie werd uitgerekend als de
wortel van iets.
Neem de drie standaarddeviaties in het kwadraat, dan krijg je
0,707 en 0,666 en 1,374.
Waarschijnlijk valt nu op dat die laatste de som van die andere twee is
(het kleine verschil komt door afrondfouten).
Ofwel:
σsom2 =
σ12 +
σ22 . Kortom: |
| |
|
|
Esom = E1 +
E2
+ ...
σsom2 =
σ12 +
σ22 + ... |
|
| |
|
| Een (nogal lastig) bewijs dat dat
altijd zo is staat hiernaast. Daarvoor moet je nog wel weten hoe die
standaarddeviatie ook alweer werd berekend... |
| |
 |
|
Speciaal geval: Dezelfde dingen bij elkaar optellen. |
| |
|
| Dat komt erg vaak voor, namelijk
elke keer als je een "experiment" vaker uitvoert. Een eenvoudig
voorbeeld is bijvoorbeeld het gooien van 5 dobbelstenen en de ogen ervan
optellen. Dat is natuurlijk precies hetzelfde als vijf keer één
dobbelsteen gooien. |
Voor het gooien van één dobbelsteen is de
kansverdeling erg eenvoudig, dus zijn de verwachtingswaarde en de
standaarddeviatie makkelijk uit te rekenen.
Hiernaast zie je dat geldt E = 3,5 en
σ = 1,7078
Dan geldt voor de som van vijf dobbelstenen:
E = 3,5 + 3,5 + ... = 5 · 3,5
= 17,5
σ2 = 1,70782 +
1,70782 + ... = 5 ·
1,70782 = 14,5829 dus
σ
= 3,82
Dat gaat een stuk makkelijker dan als je een kansverdeling voor alle
vijf de stenen samen moet maken!!! |
 |
| |
|
Als we n dezelfde
dingen bij elkaar optellen geeft dat:
Esom = E1 + E2 + .... =
E + E + .... =
n · E
σsom2 =
σ12 +
σ12 + .... =
σ2 +
σ2
+ ..... = n ·
σ2 dus
σsom = √(n
· σ2)
=
σ√nDit laatste heet de
√n - wet: |
|
tel n dezelfde dingen bij elkaar
op:
Esom = nE
σsom =
σ√n
|
|
| |
|
|
De binomiale verdeling.
Dat laatste: dingen bij elkaar optellen gebeurt eigenlijk altijd
bij de binomiale verdeling. Daar werden het "aantal successen" geteld
bij n experimenten.
Als je nou de verwachtingswaarde en de standaarddeviatie van het aantal
successen bij één experiment weet, dan kun je met bovenstaande regels
voor E en
σ makkelijk uitbreiden naar n
experimenten (bij de binomiale verdeling zijn die n experimenten
allemaal gelijk, dus je telt automatisch alleen dezelfde dingen bij
elkaar op).
Laten we E en
σ voor één experiment gaan
uitrekenen.
Als de kans op succes gelijk is aan p, dan ziet de kansverdeling
daarvan er zó uit: |
| |
|
| één experiment, kans op succes p |
| aantal successen X |
kans |
0
1 |
1 - p
p |
|
| |
|
De verwachtingswaarde is dan
E = 0 · (1 - p) + 1
· p = p
Voor de standaarddeviatie gaan we de tabel uitbreiden met (X -
E) en (X - E)2 : |
| |
|
| één experiment, kans op succes p |
| aantal successen X |
kans |
(X - E) |
(X - E)2 |
0
1 |
1 - p
p |
0 - p
1 - p |
p2
(1 - p)2 |
|
| |
|
De gemiddelde kwadratische
afwijking is dan (1 - p)
· p2 + p
· (1 - p)2 = p2
- p3 + p - 2p2 + p3
= p - p2 = p(1 - p)
De standaarddeviatie bij één experiment is daar dan de wortel van:
σ = √(p(1 -
p))
Bij n dezelfde experimenten kunnen we nu de eerder gevonden
regels voor de verwachtingswaarde en de standaarddeviatie gebruiken:
Esom = n · E = n
· p en
σsom
=
σ√n = √(p(1
- p)) ·
√n
= √(np(1 - p)).
Conclusie: |
| |
|
|
voor de binomiale verdeling
geldt:
E = n
· p en
σ =
√(np(1
- p)) |
|
| |
|
|
De standaardafwijking van een
gemeten kans. |
| |
|
Het kan natuurlijk ook dat we de
kans ergens op willen bepalen.
Stel dat je 40 keer met een valse dobbelsteen gooit en 12 zessen krijgt.
Dan schat je natuurlijk de kans op 6 voor deze valse steen in op 12/40 =
0,30
Wat doe je dan eigenlijk?
Nou,. je deelt de gemeten verwachtingswaarde E door het aantal
experimenten n.
Maar als zo'n E een standaardafwijking van σ = √(np(1
- p)) heeft, dan moet je voor die berekende
p de standaardafwijking delen door n.
Dat geeft: |
|
|
| |
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
Als ik 20 dobbelstenen maak zoals
op de bouwplaat hiernaast, en ik gooi al die 20 dobbelstenen op
tafel, wat zullen dan het gemiddelde en de standaarddeviatie van
de som van al die ogen zijn? |
 |
| |
|
|
|
| |
|
|
|
| 2. |
Koos en Francien willen beiden graag een
willekeurig getal van 2 t.m.12 hebben.
Koos gooit twee dobbelstenen en telt het totaal aantal ogen.
Francien heeft een vaas met ballen, genummerd 2 t.m.12 en trekt
er willekeurig een bal uit. |
| |
|
|
|
| |
a. |
Beredeneer zonder berekening te
maken wie van beiden de grootste standaarddeviatie zal krijgen. |
| |
|
|
|
| |
b. |
Bereken beide standaarddeviaties. |
| |
|
|
|
| |
|
|
|
| 3. |
Een dronkeman staat in een lange
straat en is volledig zijn oriëntatie kwijt.
Hij neemt elke keer een stap óf vooruit, óf achteruit. Beiden
hebben kans 50%.
Neem aan dat zijn stappen allemaal even groot zijn. |
| |
|
|
|
| |
Na 10 stappen heeft hij een aantal
stappen naar voren gedaan. Het gemiddelde daarvan is uiteraard
5. |
| |
|
|
|
| |
a. |
Hoe groot is de standaarddeviatie van dit
aantal? |
|
| |
|
|
|
| |
b. |
Op een gegeven moment is de
standaarddeviatie van het aantal stappen naar voren gelijk aan
3. Hoe groot is het gemiddeld aantal stappen naar voren
op dat moment? |
| |
|
|
|
| |
Na 10 stappen heeft hij een bepaalde
afstand tot zijn beginpunt. |
| |
|
|
|
| |
c. |
Wat zijn de standaarddeviatie en de
verwachtingswaarde van die gemiddelde afstand? |
| |
|
|
|
| |
|
|
|
| 4. |
Bij een casino is de draaischijf
verdeeld in de getallen 0 tm 36
Het getal nul is groen, en van de overige 36 getallen zijn er 18
rood en 18 zwart.
Een gokker gaat naar het casino en is van plan €10,- te gaan
besteden, maar twijfelt nog over twee verschillende tactieken om
zijn geld in te zetten.
• tactiek 1: zet elke keer €1,- op zwart. Als
dat lukt krijgt hij €2,- terug van het casino, anders niets.
• tactiek 2: zet elke keer €1,- op het getal 8. Als
dat lukt krijgt hij €36,- terug van het casino, anders niets.Het geld dat
hij terugkrijgt legt hij apart en gebruikt hij dus niet om
verder mee te spelen. In totaal zal hij bij beide tactieken dus
10 keer gaan spelen. |
| |
|
|
|
| |
a. |
Bereken voor beide tactieken de
verwachtingswaarde en de standaarddeviatie van het totale bedrag
dat de gokker na 10 keer spelen apart zal hebben gelegd. |
| |
|
|
1:
9,73 en 3,16
2: 9,73 en 18,46 |
| |
b. |
Het casino heeft natuurlijk het
liefst een vaste stabiele bron van inkomsten. Welke tactiek zal
het casino daarom het liefst bij zijn klanten zien? Geef
een wiskundige uitleg en maak daarin gebruik van het begrip
standaarddeviatie. |
| |
|
|
|
| 5. |
Iemand heeft een
verzameling van 6 dobbelstenen waar je 1 tm 8 mee kunt gooien
plus nog 3 dobbelstenen waar je 1 tm 4 mee kunt gooien, zoals je
in het plaatje hiernaast ziet. Als je al deze 9 dobbelstenen
in één keer gooit, en het totaal aantal ogen telt, wat zijn dan
de verwachtingswaarde en de standaarddeviatie van het aantal
ogen?
|
 |
| |
|
|
|
| 6. |
a. |
Zes voetbalvrienden hebben naar een
wedstrijd elk een aansteker, een tomaat en een ei meegenomen om
naar de scheidsrechter te gooien. Bij de eerste in hun
ogen foute beslissing gooien ze alle zes één van hun voorwerpen
naar de scheidsrechter.
X is het aantal eieren dat er op dat moment gegooid wordt.
Bereken de verwachtingswaarde en de standaarddeviatie van X. |
| |
|
|
|
| |
b. |
Een voetbalfan heeft naar een
wedstrijd een zak met 4 aanstekers, 4 tomaten en 4 eieren
meegenomen om naar de scheidsrechter te gooien. Bij de in zijn
ogen eerste foute beslissing gooit hij vier willekeurig gekozen
voorwerpen uit zijn tas naar de scheidsrechter.
X is het aantal eieren dat hij op dat moment gooit.
Bereken de verwachtingswaarde en de standaarddeviatie van X. |
| |
|
|
|
| |
|
|
|
| |
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|