| |
 |
| |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
De standaardnormale verdeling. |
|
|
| |
|
|
|
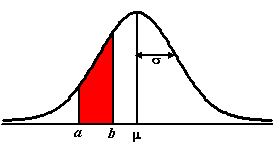
| Die normale verdeling
is eigenlijk maar knap lastig, om een oppervlakte uit te rekenen heb je
een gemiddelde m nodig en een
standaarddeviatie
σ, en een ondergrens en een
bovengrens, en dan pas kun je aan 't rekenen. Niet iets wat je zomaar
even in een tabelletje opzoekt. |
 |
| |
|
Als je dat zou willen moet je
voor elke
μ en
σ
combinatie een aparte tabel maken. Dat worden er nogal veel. Daarom gaan
we deze les proberen of we niet één eenvoudige
μ-σ
tabel kunnen maken waar we dan al die anderen uit kunnen afleiden.
Dat gaat lukken! (of verraad
ik nou alles?) |
| |
|
|
|
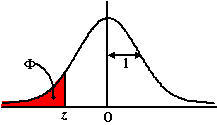
We beginnen gewoon met de
allersimpelste normale verdeling die er te verzinnen is, en dat is
die met een gemiddelde van 0 en een standaarddeviatie van 1.
Dat noemen we de "standaardnormale verdeling". De x
daarbij wordt meestal z genoemd, en de oppervlakte naar links toe
heet
Φ, zoals je in de figuur hiernaast kunt
zien.
Als je nou één tabel hebt voor allerlei z-waarden met
bijbehorende
Φ, dan kun je daaruit alle
andere normale verdelingen afleiden. |
 |
| |
|
|
|
Om dat te doen gaan we
gewoon een willekeurige normale verdeling (met
μ
en
σ) stap voor stap veranderen in de
standaardnormale verdeling. Dat gaat in twee stappen, en laten we
daarbij in de gaten houden wat er met een willekeurige x gebeurt.
• Eerst schuif je de klokvorm m naar
links. Dan komt die x terecht bij x - μ
• Daarna maak je de afstand van elk punt tot de y-as
1/σ keer zo groot. Dan
komt die x - μ terecht
bij 1/σ
• (x
-
μ)
Hieronder zie je wat er gebeurt (met als voorbeeld
μ > 0 en
σ > 1,
maar met andere waarden gaat het precies zo). |
| |
|
|
|
|
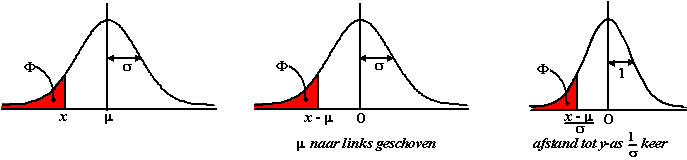 |
| |
|
|
|
Daar rechts is de
standaardnormale verdeling verschenen.
En het mooie is: omdat die
Φ een
percentage voorstelt (de rode oppervlakte als percentage van de totale
oppervlakte) is die niet veranderd. Het percentage rood in de
rechterfiguur is gelijk aan dat in de linkerfiguur.
Conclusie: een willekeurige normale verdeling met
μ en
σ geeft
bij een bepaalde x-waarde dezelfde oppervlakte naar links als de
standaardnormale verdeling bij z = (x -
μ)/σ. |
| |
|
|
|
|
|
| |
|
|
|
|
De Grafische Rekenmachine. |
| |
|
|
|
Op de TI kun je natuurlijk gewoon
voor de standaardnormale verdeling gebruiken normalcdf(a, b,
0, 1). Er is echter ook een "omgekeerde" berekening en dat gaat met de
optie invNorm. Die vind je bij
2nd
-
distr
- 3: invNorm(
Als je achter invNorm een percentage intoetst (een oppervlakte
Φ), dan geeft de GR je als antwoord bij welke
waarde van z dat percentage vanaf links van de klokvorm wordt
bereikt. Dus invNorm(Φ) = z |
 |
| |
|
|
|
|
| |
|
|
|
Dat heeft als
voordeel dat je, als je een oppervlakte weet, niet dat hele gedoe met
intersect hoeft te gebruiken. Het heeft alleen als nadeel dat je de
gevonden z wel weer moet omrekenen naar een x.
Voorbeeld.
Het gemiddelde CSE cijfer Wiskunde was vorig jaar een 6,4 met een
standaarddeviatie van 1,6
Welk cijfer moet je gehaald hebben om bij de beste 20% van Nederland te
horen?
Als je bij de beste 20% hoort, dan heb je 80% achter je gelaten, en
daarbij hoort invNorm(0,80) = 0,8416 = z
Dus (x - 6,4)/1,6 = 0,8416
⇒ x - 6,4 = 1,3466
⇒ x = 7,746 dus je moet
minstens een 7,8 hebben gehaald. |
| |
|
|
|
Wááááát? Is dat alles?
Moet ik daar deze hele les voor leren??
Kon ik ook met Intersect!!! |
| |
|
|
|
Rustig, rustig, neem
even een slokje water.
Er zijn ook vragen die je alleen maar met deze invNorm kunt oplossen.
Dat zijn problemen waarbij zowel
μ als
σ onbekend zijn.
|
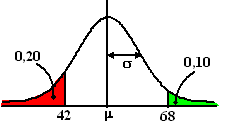
Neem de klokvorm hiernaast.
Onder de x = 42 zit 20% en boven de x = 68 zit 10%.
Met alleen maar normalcdf kun je nu niet berekenen wat
m en s zijn.
Maar met invNorm kan het wél. kijk maar:
invNorm(0,20) = -0,8416 = (42 -
μ)/σ
ofwel -0,8416σ = 42 -
μ
invNorm(0,90) = 1,2816 = (68 -
μ)/σ
ofwel 1,2816σ = 68 -
μ. |
 |
| |
|
|
|
Dat zijn twee
vergelijkingen met twee onbekenden, en die zijn makkelijk op te lossen.
Maak bijvoorbeeld van de eerste
μ = 42 +
0,8416σ en vul dat in in de tweede.
Dat geeft 1,2816σ = 68 - 42 - 0,8416σ
⇒ 2,1232σ =
26 ⇒
σ = 12,25
Dan is
μ = 42 + 0,8416 • 12,25 = 52,31 |
| |
|
|
|
Zo.
Tevreden?
Toch nog wat geleerd?? |
| |
|
|
|
| |
|
|
|
|
|
|
OPGAVEN |
| |
|
|
|
|
|
| 1. |
Het aantal pagina's dat je met een blauwe BIC
vulpen kunt schrijven is normaal verdeeld met een gemiddelde van
360 en een standaarddeviatie van 24.
Bereken via de standaardnormale verdeling hoe groot de kans is
dat het aantal pagina's bij een willekeurige pen tussen de
330 en 340 ligt.
|
| |
|
|
|
|
|
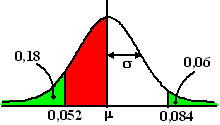
| 2. |
a. |
Bereken
μ
en
σ bij de volgende normale
verdeling: |
| |
|
 |
| |
|
|
|
|
|
| |
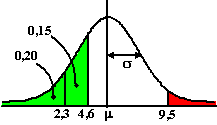
b. |
Bereken het rood gekleurde gebied
bij de volgende normale verdeling |
| |
|
 |
| |
|
|
|
|
|
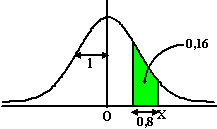
| 3. |
Bereken de waarde van X hieronder
als de groene oppervlakte gelijk is aan 16%. |
| |
|
|
|
|
|
| |
 |
| |
|
|
|
|
|
| 4. |
Heb je bij vraag 1 aan de
continuïteitscorrectie gedacht? Zo nee, maak de vraag dan
nog een keer en nu goed graag! |
| |
|
|
|
|
|
| 5. |
Examenvraagstuk VWO Wiskunde B,
2005 De snelheidsmeter van een auto geeft meestal
niet precies aan wat de werkelijke snelheid is waarmee de auto rijdt. Voor
een bepaald type snelheidsmeter geldt het volgende: als de snelheidsmeter
een snelheid van v km/u aangeeft is de waarde van de werkelijke
snelheid normaal verdeeld, waarbij het gemiddelde gelijk is aan v
en de standaardafwijking gelijk is aan 1,5% van dat gemiddelde.
Bij snelheidscontrole wordt een marge aangehouden van 3%. Dus
bijvoorbeeld bij een maximumsnelheid van 100 km/u wordt er beboet bij
snelheden van 103 km/u en hoger.
Van een auto is de snelheidsmeter van bovenstaand type. De
bestuurder rijdt volgens de meter steeds met precies de toegestane
maximumsnelheid.
Stel dat de toegestane maximumsnelheid 70 km/u is. De kans dat de
werkelijke snelheid van de bestuurder zo groot is dat hij voor een boete
in aanmerking komt is dan, afgerond op 3 decimalen, gelijk aan 0,023.
|
| |
|
|
|
|
|
| |
a. |
Toon dit aan. |
|
|
|
| |
|
|
|
|
|
| |
De kans dat hij in aanmerking komt voor een
boete is bij elke toegestane maximumsnelheid even groot |
| |
|
|
|
|
|
| |
b. |
Toon dit aan. |
|
|
|
| |
|
|
|
|
|
| |
De bestuurder passeert in een jaar 200 keer
een elektronisch bord dat waarschuwt wanneer men te hard rijdt, dat wil
zeggen wanneer men de boetegrens overschrijdt. De kans dat de bestuurder
voor een boete in aanmerking komt is telkens 0,023. |
| |
|
|
|
|
|
| |
c. |
Bereken de kans dat de bestuurder van die 200 keer meer
dan 2 keer gewaarschuwd wordt. |
| |
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |