|
|||||
| 1. | Het aantal pagina's
is een discrete variabele, dus je moet de continuďteitscorrectie
gebruiken. Tussen 330 en 340 wordt dan tussen 330,5 en 339,5 330,5 geeft z = (330,5 - 360)/24 = -1,229 339,5 geeft z = (339,5 - 360)/24 = -0,854 normalcdf(-1.229, -0.854, 0, 1) = 0,0870 |
||||
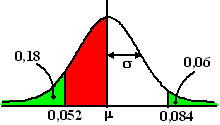
| 2. | a. | invnorm(0,18) = -0,9154 =
(0,052 -
μ)/σ
dus -0,9154σ = 0,052 -
μ invnorm (0,94) = 1,555 = (0,084 - μ)/σ dus 1,555σ = 0,084 - μ Daaruit volgt μ = 0,052 + 0,9154σ en μ = 0,084 - 1,555σ gelijkstellen: 0,052 + 0,9154σ = 0,084 - 1,555σ 2,4704σ = 0,032 σ = 0,013 en dan is μ = 0,0639 |
 |
||
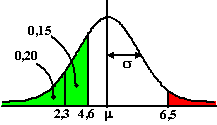
| b. | invnorm(0,20) = -0,8416 =
(2,3 -
μ)/σ
dus -0,8416σ = 2,3 -
μ invnorm (0,35) = -0,3853 = (4,6 - μ)/σ dus -0,3853σ = 4,6 - μ Daaruit volgt μ = 2,3 + 0,8416σ en μ = 4,6 + 0,3853σ gelijkstellen: 2,3 + 0,8416σ = 4,6 + 0,3853σ 0,4563σ = 2,3 σ = 5,04 en dan is μ = 6,68 De rode oppervlakte is normalcdf(9.5, 1099, 6.68, 5.04) = 0,29 |
 |
|||
| 3. | μ
= 0 en
σ = 1 dus dit is de standaardnormale
verdeling. er geldt invnorm(Φ) - invnorm(Φ - 0,16) = 0,8 Y1 = invnorm(Φ) - invnorm(Φ - 0,16) Y2 = 0,8 intersect levert Φ = 0,2166 of Φ = 0,9433 invnorm(0,2166) = -0,78 en invnorm(0,9433) = 1,58 Die laatste zal X dus, gezien de figuur, zijn. |
||||
| 4. | Ja, ik had er gelukkig aan gedacht. | ||||
| 5. | a. | P(boete) = P(v > 72,1) = normalcdf(72.1, ∞ , 70, 1.05) ≈ 0,02275 ≈ 0,023 | |||
| b. | z = (x
-
μ)/σ Noem de maximumsnelheid v, dan geldt: x = 1,03 • v en μ = v en σ = 0,015v Dat geeft z = (1,03v - v)/(0,015v) = 0,03v/0,015v = 2 Omdat z altijd gelijk is, is de oppervlakte onder de klokvorm dat ook. |
||||
| c. | binomiale verdeling
met n = 200, p = 0,023 P(meer dan 2) = 1 - P(2 of minder) = 1 - binomcdf(200, 0.023, 2) ≈ 0,84 |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||