somrijen


Somrijen	© h.hofstede (h.hofstede@hogeland.nl)

Soms is het niet zo interessant hoe groot elk getal in een rij apart is, maar meer hoe groot alle getallen samen zijn.
Neem een schaatser die een 10 km aan het schaatsen is. Zo'n 10 km bestaat uit 25 rondjes van 10 km, en bij elk van die rondjes wordt de rondetijd gemeten.
Dat geeft dus een rij met 25 rondetijden. Het is eigenlijk helemaal niet zo interessant hoe groot al die tijden apart zijn, maar meer hoeveel ze bij elkaar opgeteld opleveren, immers dat is de totale eindtijd van de schaatser.

Tijdens zijn wereldrecord in Salt Lake City 2007 schaatste Sven Kramer de volgende rondetijden:

nr. i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
tijd t_i	33,13	29,85	30,42	30,13	30,20	30,25	30,48	30,35	30,63	30,36	30,53	30,55	30,61	30,73	30,75	30,57	30,60	30,37	30,57	30,53	30,38	29,99	30,25	29,81	29,65

Het wereldrecord is dus gelijk aan al die getallen opgeteld. (Het was trouwens 12:41,69)

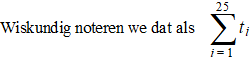Over deze notatie kun je in deze les meer vinden, voor nu is het even niet zo belangrijk.
In deze les richten we ons op wat regelmatiger rijen en hoe je daarvan de som met je GR kunt berekenen.
Stel bijvoorbeeld dat een schaatser begint met een rondje van 33 seconden en daarna een oplopend schema heeft: elk volgend rondje is 0,2 seconden langzamer dan de vorige.
Dat levert dus de rondetijden: 33,0 - 33,2 - 33,4 - 33,6 enz op.
Kijk daar kunnen we wat mee. Wij wiskundigen herkennen daarin uiteraard direct een rekenkundige rij.

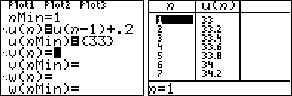
Die kunnen wij natuurlijk makkelijk in onze rekenmachine invoeren, zoals hiernaast.

Maar de vraag is dan natuurlijk:

Hoe bepaal je de som van die termen?

Nou dat kan door een tweede rij v_n te maken die steeds de termen van u_n optelt. Dat gaat met de volgende recursievergelijking:

v_n = v_n_-1 + u_nmet v₀ = 0

Immers op deze manier tel je steeds de laatste u_n op bij alle vorigen (die staan in v_n_-1). De som van de eerste n-1 termen staat nu in v_n. Als je kiest nMin = 0 dan staat de som van de eerste n termen in v_nHiernaast zie je dat dat een eindtijd van v₂₅ = 923 seconden (15:33,00) oplevert voor de schaatser.

In de volgende twee lessen zullen we ook een algebraïsche manier vinden om de som van een rekenkundige en een meetkundige rij te berekenen.

OPGAVEN

Bereken de som van de eerste 20 termen van de volgende rijen:

u_n = 0,9u_n_-1 + 2 met u₁ = 10

312,16

u_n = 2n + 0,5√(u_n_-1) met u₁ = 3

463,76

Bereken 1² + 2² + 3² + 4² + ... + 30²

9455

Iemand opent op 1 januari een bankrekening en stort daar €200,- op. De bank geeft hem 4% rente per jaar, en die rente wordt op 31 december bijgeschreven. Elk jaar op 1 januari stort de man wéér €200,- op de rekening.
Na hoeveel jaar heeft hij in totaal €2723,60 rente gekregen?

22 jaar

Een roddel verspreid zich in het begin heel snel, en daarna steeds langzamer. Dat komt natuurlijk omdat steeds meer mensen er al van op de hoogte zijn, en dus komen er steeds minder nieuwen bij.
De volgende vergelijking blijkt te gelden voor het aantal mensen A_n dat de n^de dag de roddel voor het eerst hoort:

A_n = ^{(200n + 1000)}/_{(n²
+ 100)}

Neem aan dat de eerste dag 50 mensen de roddel, kennen.
We nemen voor deze opgave voor het gemak aan dat het aantal mensen geen geheel getal hoeft te zijn.

Hoeveel mensen zijn na 18 dagen op de hoogte van de roddel?

261

Bereken 1 + ¹/₂ + ¹/₃ + ¹/₄ + ... + ¹/₁₀₀ in zes decimalen nauwkeurig.

5,187378

olympiadevraagstuk
In een vierkant met zijden √2 beginnen we in een hoekpunt met punt a₁ en we tekenen daarna steeds een volgend punt op een diagonaal zodat de afstand tot het middelpunt M gehalveerd wordt.

Wat wordt de lengte van de "spiraal" die we zo krijgen als we oneindig lang doorgaan? Geef je antwoord in drie decimalen nauwkeurig.

2,236