|
|
 |
|
Rijen met de GR. |
ฉ
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
Een voordeel van
recursievergelijkingen is dat ze vaak erg eenvoudig zijn. Maar ze hebben
ook een groot nadeel. Dat is dat je niet z๓maar een getal uit de rij
kunt uitrekenen; dat kan pas als je alle vorige getallen ook eerst
uitrekent.
Dat kan nogal een werk zijn..... |
Gelukkig springt daar onze TI-83
ons te hulp. Die heeft een manier om te rekenen met recursievergelijkingen, en dat gaat als volgt:
Druk op MODE
en zet de vierde regel op
Seq
Druk op
Y=
en je ziet het scherm hiernaast.
Om nu een rij un in je rekenmachine te zetten moet je
drie dingen invoeren:
|
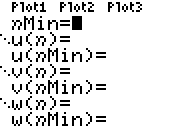
|
nMin.
Daar moet staan welk nummer het eerste getal
van je rij heeft. Dat zal dus meestal nummer 0 of nummer 1 zijn.
u(n)
=
Daar voer je je recursievergelijking in. De n is nu de
knop
X,T,q,n
geworden en de u vind je bij
SHIFT
-
7
u(nMin)
=
Daar komt te staan hoe groot het eerste getal van je rij is. |
| |
Laten we onze torens-van-Hanoi-rij gaan
invoeren.
Die zag er z๓ uit: 1 - 3 - 7 - 15 - 31 - .....
En de recursieformule was un = 2 un
-1 + 1
Als we het eerste getal uit de rij nummer 1 noemen (een toren van 1
schijf) dan moet je dus invoeren:
nMin = 1
u(n) = 2 * u(n - 1) + 1
u(nMin) = 1
zoals hiernaast is gedaan. |
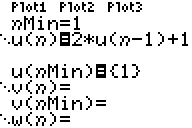 |
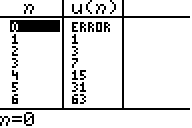
Kijk nu bij TABLE en je krijgt de rij getallen
in beeld.
(als je een andere tabel krijgt kun je die uiteraard met TBLSET
aanpassen) |
|
u0 is er
uiteraard niet, want onze rij begon immers bij nMin = 1
Verder staan daar inderdaad de getallen uit deze rij. Mooi. Dat klopt.
Er is een legende over een Vietnamese tempel waar priesters dag in dag
uit bezig zijn zo'n toren van 64 gouden schijven op deze manier te
verplaatsen. En als dat werk volbracht is, dan is dat het einde van onze
wereld!!!!
Nou, laten we dat dan maar gauw uitrekenen! |
|
| Bereken met behulp van jouw tabel hoe lang
deze priesters bezig zullen zijn als ze ้้n schijf per seconde
verplaatsen. (het gaat wat sneller als je met TBLSET het begin van je
tabel op Tblstart = 64 zet). |
|
| Vergelijk de gevonden tijd met de
leeftijd van onze aarde (ongeveer 4,5 109 jaar) en kijk of
we ons al zorgen moeten gaan maken....... |
| |
|
|
|
|
| Er is ook een manier om
een rij in de mode Func van je GR direct te krijgen, maar die is
niet zo heel belangrijk. Als het er meer over wilt weten moet je
deze les van de GR doornemen. |
| |
|
|
|
|
|
Meerdere rijen in voeren. |
| |
|
|
|
|
Net als bij u(n)
kun je ook tegelijk rijen bij v(n) en
w(n) invoeren, maar ze moeten wel met hetzelfde
nummer beginnen. Daarom kun je alleen nMin in het begin
invoeren voor alle rijen tegelijk.
Wat heb je daaraan?
Dat kun je gebruiken om
rijen met elkaar te vergelijken
rijen van elkaar af te laten hangen.
de som van een rij getallen uit te rekenen. |
Vooruit dan maar; van alle drie een voorbeeldje:
Voorbeeld 1.
Jan begint met een maandsalaris van
600 en krijgt elk
jaar eerst een opslag van 6% en daarna nog eens
50,-
Kees begint met een maandsalaris van
1000 en krijgt elk jaar
eerst een opslag van 4% en daarna nog eens
60,-
Wanneer verdient Jan meer dan Kees?
nMin = 0
u(n) = 1,06 * u(n - 1) + 50
u(nMin) = 600
v(n) = 1,04 * v(n - 1) + 60
v(nMin) = 1000
Kijk wanneer u(n) groter is dan
v(n). Dat is vanaf n = 23
Voorbeeld 2.
Natasja en Kim gaan om de beurt getallen
noemen.
Kim noemt steeds het vorige getal van Natasja, maar
vermenigvuldigt met 5 en daarna 3 er afgetrokken.
Natasja noemt steeds het vorige getal van Kim, maar dan
vermenigvuldigd met 2 en daarna 1 er bij opgeteld.
Natasja begint met het getal 12, dus Kim zegt daarna 57, en
Natasja daarna 115
Wat is het tiende getal dat Natasja noemt?
nMin = 1
u(n) = v(n - 1) 5 - 3
(de getallen van Natasja)
u(nMin) = 12
v(n) = u(n - 1) 2 + 1
(de getallen van Kim)
v(nMin) = 57
TABLE: u(10) = 2822222
Voorbeeld 3.
Bereken √1
+ √2 +
√3 + ... +
√100
Voer de rij un in met
nMin = 1, u(n) =
√(n), u(nMin)
= 1
Als je nu daarna invoert de rij vn
met v(n) = v(n - 1) + u(n
- 1) met v(nMin) = 0, dan staat daar
eigenlijk dat v(n) gelijk is aan de vorige v
plus √n (want dat is
u). Dus er wordt steeds weer
√n opgeteld bij de
vorige som.
Je vindt de som van de eerste 100 wortels dan in v(101)
(het is trouwens ongeveer gelijk aan 671,46) |
| |
|
Denk erom
dat achter het = teken van de
recursievergelijking
alleen termen met n - 1, n - 2, enz.
mogen staan.
Er mag nooit een u(n) of v(n)
aan de rechterkant van zo'n vergelijking staan!! |
|
| |
|
|
|
|
| 1. |
Gegeven is de rij getallen un
= √(3 +
un - 1) met u1
= 400000 |
| |
|
|
|
|
| |
a. |
Bereken u9
van deze rij getallen in drie decimalen nauwkeurig. |
|
| |
|
|
|
| |
b. |
Onderzoek wat er zal
gebeuren met un als je alsmaar doorgaat. |
|
| |
|
|
|
| |
c. |
Onderzoek met je GR of het resultaat
van vraag b) afhangt van het begingetal u1 |
|
| |
|
|
|
|
| |
Er is een grappige manier om het
getal van vraag b) en c) exact te berekenen. |
| |
Click als je het leuk vindt dat te
onderzoeken op de verdieping hiernaast. |
|
| |
|
|
|
 |
| |
|
|
|
|
| 2. |
Gegeven is de recursievergelijking
un = 3,5 un - 1
(1 - un - 1) met
u1 = 0,1 |
| |
|
|
|
|
| |
a. |
Bereken u25 in
vier decimalen nauwkeurig. |
|
|
| |
|
|
|
| |
b. |
Onderzoek hoe de rij verloopt.
Je moet ver genoeg in de rij gaan (tot ongeveer nummer 40) om te
zien wat er op den duur gebeurt. |
| |
|
|
|
|
| 3. |
Bij een antibioticakuur moet een
pati๋nt eerst (op dag 0) een tablet van 200
mg innemen en daarna om de 24 uur weer een nieuwe tablet van 200
mg. Het lichaam breekt elke 24 uur echter ook 30% van de
hoeveelheid medicijn in het bloed af. |
| |
|
|
|
|
| |
a. |
Geef een recursievergelijking die de
hoeveelheid medicijn in het lichaam om de 24 uur weergeeft
direct na het innemen van een tablet. |
| |
|
|
|
|
| |
Het medicijn werkt pas goed als er
minstens 600 mg in het lichaam aanwezig is. |
| |
|
|
|
|
| |
b. |
Na hoeveel dagen is dat voor het
eerst het geval? |
|
| |
|
|
|
|
| |
Echter als er meer dan 650 mg
aanwezig is, dan heeft dat nadelige bijwerkingen. |
| |
|
|
|
|
| |
c. |
Onderzoek bij welke tabletgrootte
elke 24 uur de grens van 650 mg niet wordt overschreden maar de
grens van 600 mg wel wordt gehaald. |
|
| |
|
|
|
|
| 4. |
Bekijk de volgende rij breuken:
2/3, 5/7,
11/15, 23/31,
47/63, ....
Onderzoek met je GR of deze rij breuken uiteindelijk een
constante waarde zal aannemen. |
| |
|
|
|
|
| 5. |
Gegeven is de rij un+1
= n ื un
met u1 = 1.
Bereken u10
Waar ken je deze rij getallen van? |
| |
|
|
|
|
|
|
|
|
Tweede-orde vergelijkingen |
|
|
Als un niet
alleen van un-1 afhangt, maar ook van un
- 2, dan kun je deze rij ook in je GR invoeren, maar dan moet je
wel TWEE beginwaarden invoeren. Zo'n vergelijking heet dan een
recursievergelijking van de tweede orde.
Dat doe je door bij unMin het tweede getal en het
eerste uit de rij tussen te zetten, in die volgorde!!,
gescheiden door een dikke komma (die boven de 7 op je GR zit). |
De beroemdste tweede-orde vergelijking die er
bestaat is zonder twijfel de rij van Fibonacci:
| |
| 1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - .... |
| |
Elk volgend getal vind je door de twee vorigen bij elkaar op te
tellen, dus de recursievergelijking is un = un
- 1 + un - 2 en de
twee begingetallen zijn {1, 1}
Hiernaast zie je hoe die rij in de GR is ingevoerd. |

|
De Fibonacci-rij komt op allerlei plaatsen tevoorschijn. De bekendste is
misschien wel het aantal konijnenparen |
|
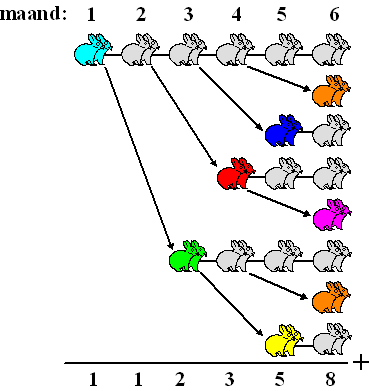
| Een paar konijnen van een maand oud is nog
te jong om zich te kunnen voortplanten. Maar vanaf de tweede maand
krijgt het paar elke maand twee jongen, die zich op hun beurt na twee
maanden eveneens gaan voortplanten met twee jongen per maand, enz. Dat
geeft zoiets: |
| |
|
|
 |
| |
|
| Die gekleurde konijnenparen zijn dus
"nieuwelingen"die net geboren worden, alle grijze paren zijn gewoon
konijnen die steeds ouder worden. |
| |
|
|
|
| 6. |
De Lucasrij heeft dezelfde recursievergelijking
als de rij van Fibonacci, maar hij begint niet met 1 en 1 maar
met 1 en 3. Bereken het 40ste getal van de Lucasrij. |
| |
|
|
|
|
| 7. |
Gegeven is de recursievergelijking
un = 0,5un - 1
+ 1,2un - 2
met u0 = 2 en u1 = 3 |
| |
|
|
|
|
| |
a. |
Bereken u30 in
twee decimalen nauwkeurig. |
|
| |
|
|
|
| |
b. |
Je kunt u0 eentje
verhogen, maar ook u1.
Onderzoek welk van beide acties de grootste u10
oplevert. |
|
| |
|
|
|
|
| 8. |
Examenvraagstuk VWO Wiskunde A,
2008. Drogisterijketen
Haarsma verkoopt Hagelwit tandpasta. Aan het eind van elke maand
koopt Haarsma deze tandpasta in bij de groothandel. Haarsma moet daarvoor
elke maand een schatting maken van het aantal tubes dat hij de volgende
maand zal verkopen. In de bedrijfskunde worden
verschillende methoden gebruikt om zon schatting te
maken. Een van die methoden komt in deze opgave aan de orde. In
zeker jaar heeft Haarsma in januari 5200 tubes verkocht en in februari
4000.
Een eenvoudig model om de verkoop voor de komende maanden te schatten is
het volgende: neem het gemiddelde van de verkoop in de twee
voorafgaande maanden. In een formule:
Vn + 2 = 1/2 Vn
+ 1 + 1/2 Vn,
met V1 = 5200 en V2 = 4000
Hierbij is Vn
het aantal verkochte tubes tandpasta in maand n,
waarbij n = 1 overeenkomt met januari.
Volgens dit model verwacht Haarsma in maart 4600 tubes te verkopen.
Als we aannemen dat de schatting steeds de werkelijke
verkoop in die maand is, kunnen we met dit model ook
de verkoop van de volgende maanden uitrekenen. Dat
betekent hier dat er in maart inderdaad 4600 tubes tandpasta verkocht
worden. En met de getallen 4000 van februari en 4600 van
maart kun je met de formule weer de verkoop
van april berekenen, enzovoort. |
| |
|
|
|
|
| |
a. |
Bereken
het aantal tubes tandpasta dat volgens dit model in juni wordt verkocht. |
| |
|
|
|
|
| |
Soms besluit men
de laatste maand zwaarder te laten meetellen dan de voorlaatste
maand. Bij de schatting voor de maand maart telt men bijvoorbeeld
februari voor 60% mee en januari
voor 40%. De formule wordt dan:
Vn+2 =
0,6Vn+1 + 0, 4Vn
, met V1
= 5200 en V2
= 4000
Als met dit
model een groot aantal maanden wordt doorgerekend, komen de waarden
van V steeds dichter bij de evenwichtswaarde
4343 te liggen. Dat betekent dat na een aantal
maanden de schattingen minder dan 1% van 4343 zullen
afwijken. |
| |
|
|
|
|
| |
b. |
Bereken in
welke maand de schatting voor het eerst minder dan 1% van 4343 afwijkt. |
| |
|
|
|
|
| |
|
|
|
|
| 9. |
Toen er nog
geen rekenmachines waren, moesten wiskundigen zo af en toe de
wortel uit een getal met pen en papier berekenen. Een goeie
methode daarvoor was de volgende;
Stel dat je √n wilt
berekenen:
gok een begingetal B
bereken n/B
neem het gemiddelde van dit laatste getal en je vorige
getal, en gebruik dat als nieuw begingetal B.Zo geeft
√57 met de begingok B = 7:
B = 7 ⇒ 57/7
= 8,1428...
(8,1428... + 7)/2 = 7,5714....
B = 7,5714... ⇒ 57/7,5714...
= 7,5283....
(7,5283... + 7,5714...)/2 = 7,5498...
B = 7,5498... ⇒ 57/7,5498...
= 7,549803...
enz.
Bereken de tiende benadering van
√57 met je GR. |
| |
|
|
|
|
 |
|
|
|
|
ฉ
h.hofstede (h.hofstede@hogeland.nl) |
 |