| |
 |
| Rekenen
met machten (1) |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
Voor je verder kunt met
exponentiλle systemen moet je eerst een paar eenvoudige
basisberekeningen met machten kennen en kunnen gebruiken.
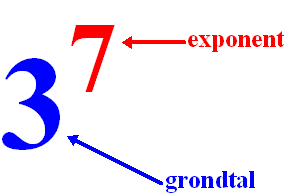
Eerst wat namen: het getal dat op de grond staat heet het GRONDTAL
en het getal dat in de lucht hangt heet de EXPONENT. |
|
|
|
| 1. machten
vermenigvuldigen. |
|
|
|
Met getallen is het simpel: 35 34
= (3 3 3 3 3) (3 3 3 3) = 3 3 3
3 3 3 3 3 3 = 39
Waar komt het op neer: Als de grondtallen gelijk zijn kun je
machten die met elkaar worden vermenigvuldigd samennemen. Dat doe je
door de exponenten op te tellen. In formule: |
|
|
|
|
|
|
|
Andersom kan het ook: als de machten gelijk zijn
maar de grondtallen verschillend kun je ze ook samennemen,
bijvoorbeeld: 34 24 = 3 3 3
3 2 2 2 2 = (3 2) (3 2) (3 2) (3
2) = 6 6 6 6 = 64
In formulevorm: xa ya = (xy)a.
|
|
|
| 2. machten van machten. |
|
|
|
Als je iets tot-de-macht doet, en dan het resultaat wιιr
tot de macht gebeurt er dit:
(32)4 = (iets)4 = (iets) (iets)
(iets) (iets) = 32 32 32
32 = (3 3) (3 3) (3 3) (3 3)
= 38
Je ziet dat je in dit geval de exponenten met elkaar moet
vermenigvuldigen: |
|
|
|
|
| |
|
|
OPGAVEN |
|
|
| 1. |
Schrijf de volgende uitdrukkingen in de vorm y
= B gx en zo eenvoudig mogelijk: |
|
| a. |
y = 4 32x
|
|
f. |
y = 0,22x + 3 |
|
| b. |
y = 0,5 4x +
2 |
|
g. |
y = 20 34x + 5 |
|
| c. |
y = 3 22x
2 |
|
h. |
y = 2x 22x
4 |
|
| d. |
y = 5 4x 4x
+ 1 |
|
i. |
y = 6x 3 6x+1 |
|
| e. |
y = 3 1,82x
6 1,8x + 1 |
|
j. |
y = 4 3x + 3x
+ 2 |
|
|
|
|
| 2. |
Examenopgave HAVO Wiskunde B,
2010
De functies f en g zijn gegeven door
f(x) = 24x + 1 en g(x)
= 4 4x
Bereken op algebraοsche wijze de coφrdinaten
van het snijpunt van de grafieken van f en g. |
| |
|
|
|
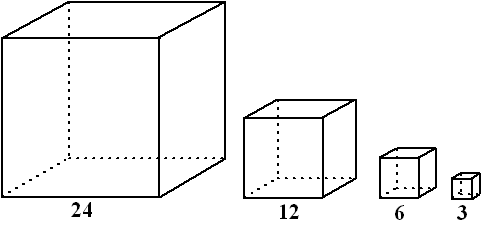
| 3. |
De volgende serie kubussen ontstaat door te
beginnen met een kubus met ribben 24, en daarna bij elke volgende kubus
de lengte van die ribben te halveren |
|
|
|
|
|
|
|
Als we de kubussen nummers 0-1-2- enz. geven,
dan geldt voor de inhoud van kubus nummer n de formule:
I(n) = 13824 0,125n
Toon aan dat dat zo is. |
|
|
| 4. |
Los op zonder rekenmachine te gebruiken:
|
| 39 + 39 + 39 = |
|
| |
a. 310
b. 99
c. 279
d. 327
e. 49 |
|
| |
|
| 5. |
Schrijf zo eenvoudig mogelijk als ab: |
| |
|
|
|
| |
a. |
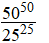 |
|
|
|
|
| |
|
|
|
| 6. |
Waaraan is 88 gelijk? |
|
| |
|
a. de
tweede macht van 44
b. de derde macht van 44
c. de vierde macht van 44
d. de achtste macht van 44
e. de zestiende macht van 44
|
|
| |
|
|
|
| 7. |
Welke van de volgende vijf is niet gelijk aan de overige
vier? |
| |
|
| |
(24)8
en (42)8 en 216
162 en 216 216
en 48 48 |
| |
|
|
|
| 8. |
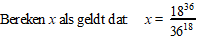 |
| |
|
|
|
| 9. |
Hoeveel
gehele waarden van x voldoen aan: 3x
+ 7 9x
+ 4 = 27x + 5 |
| |
|
|
|
| 10. |
Wat is de kleinste waarde voor n (een positief geheel getal)
waarvoor geldt dat n300 > 3500 ? |
| |
|
|
|
| 11. |
Stel dat geldt: 2a = 3b = 6
Toon aan dat daaruit volgt a + b = ab |
| |
|
|
|
| 12. |
Als xx = 5 waaraan is dan 5x5x
gelijk?
a. 52
b. 53
c. 54
d. 55
e. 56 |
| |
|
|
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
 |
| |
|
|
|
|
|