regressie van x op y


Regressie van x op y.	© h.hofstede (h.hofstede@hogeland.nl)

Tot nu toe beschouwden we steeds regressie van y op x. Dat betekent dat we x als de onafhankelijke variabele zagen, en y de afhankelijke. Ofwel, x was de oorzaak en y het gevolg.

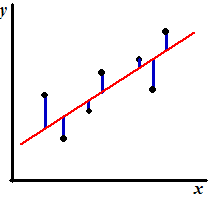
Dat had tot gevolg dat de residuen de verticale afwijkingen naar de regressielijn waren. Immers in de y-waarden zitten afwijkingen. Het plaatje hiernaast kwamen we al eerder tegen, dat hoort bij deze residuen.

Wat verandert er als we y als oorzaak beschouwen, en x als het gevolg?

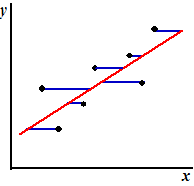
Nou, dan zijn de afwijkingen de afwijkingen in de waarden van x.
Dat betekent dat die blauwe residuen nu horizontaal lopen, zoals in de figuur hiernaast.

Hoe berekenen we hiervan de regressielijn en de correlatiecoëfficiënt?

Wacht eens even.... als we die figuur nou gewoon rechtop zetten!

Dan zijn die lijntjes weer verticaal en hebben we weer regressie zoals we gewend waren.

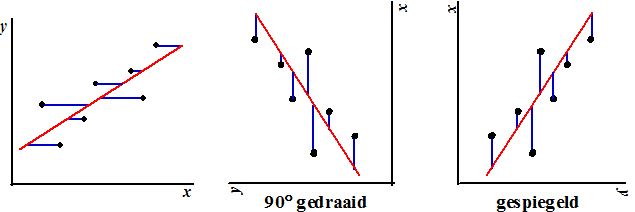
Hieronder is dat gebeurd. De figuur is 90º gedraaid (en daarna omgeklapt om de y-as weer de goede kant op te laten gaan).

Zo hebben we weer "normale" regressie gekregen. Alleen zijn de x-as en de y-as omgewisseld.
Als je dus regressie van x op y wilt bekijken dan is het recept eenvoudig:

verwissel gewoon x en y

Natuurlijk kun je ook gewoon hun namen zo laten maar in alle formules die we tot nu toe hebben afgeleid x in y veranderen en y in x. Dat zou de volgende lijst van formules geven:

Wat nog opvalt aan deze lijsten is dat de correlatiecoëfficiënt r voor beide gevallen gelijk is.
Dat is maar goed ook, immers r geeft aan hoe goed de punten op een rechte lijn liggen en dat verandert natuurlijk niet als we de puntenwolk alleen maar draaien of spiegelen.

OPGAVEN

Gegeven is de volgende tabel met meetgegevens:

x	5	6	6.5	7	7	7.5	8	8	8.5	9	10	10
y	10	13	11	10	13	12	11	14	15	13	15	16

Stel vergelijkingen op van de regressielijnen van x op y en ook van y op x

y = 0,996x + 5,073
x = 0,579y + 0,325

Bereken de voorspelling van y bij x = 7

y = 12,045

Bereken de voorspelling van x bij y = 11

x = 6,694

Ron heeft zin in een lekker middagje wiskunde, en hij gaat het volgende doen:
• Hij berekent bij x = 10 de voorspelling van y.
• Bij die voorspelde y berekent hij weer de voorspelling van x.
• Bij die x berekent hij weer de voorspelling van y.
• En zo gaat hij de hele zondag middag door....

Teken in één figuur beide regressielijnen en een aantal x en y waarden die Ron zal vinden.

Welke voorspellingen zal Ron aan het eind van zijn nuttig bestede zondagmiddag hebben?

x = 7,7108333
y = 12,75
centrale punt!

Waar zijn we dit verschijnsel eerder tegengekomen??????????(?)

regressie-effect

Van een puntenwolk is de regressielijn van y op x de lijn y = 0,8x + 3,4 en de regressielijn van x op y is
de lijn x = 0,7y + 2,1

Bereken de correlatiecoëfficiënt r

r = 0,748

Bereken x̅ en y̅
Geef je antwoord in twee decimalen nauwkeurig.

x = 29,08
y = 11,54

Als de regressielijn van y op x helling 0,8 heeft zoals hierboven, hoe groot kan de helling van de regressielijn van x op y dan maximaal zijn?

1,25