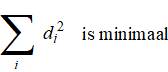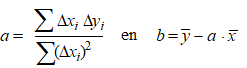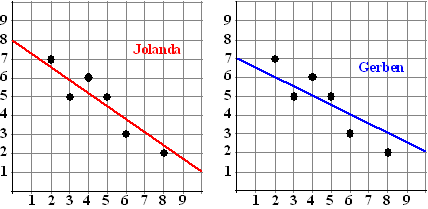
regressielijn


De regressielijn.	© h.hofstede (h.hofstede@hogeland.nl)

Woord vooraf;
Bij het bekijken van puntenwolken tot nu toe was het niet duidelijk (of maakte het niet uit) wat we op de x-as zetten, en wat op de y-as. Als je de assen zou omdraaien bleven de vormen van de puntenwolken gelijk; ze werden alleen gespiegeld in de lijn y = x.

Nu gaat dat veranderen.....

Vanaf nu gaan we ervan uit, als x en y van elkaar afhangen, dat x de oorzaak is, en y het gevolg. Dus de grootte van x "veroorzaakt" de grootte van y. Als je dat doet, dan spreken we van regressie van x op y.

regressie van x op y:
x = oorzaak, y = gevolg

(Wees gerust: later zullen we ook andere varianten bekijken).

1. Residuen.

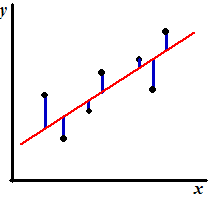
De regressielijn die we berekenen geeft de lijn die het best "past" bij onze meetgegevens. Maar wat wordt nou bedoeld met "best past" ???
Als we een regressielijn hebben gevonden, dan geeft die lijn aan welke y-waarden er het best (theoretisch) zouden passen bij de x-waarden. Maar de gemeten punten wijken natuurlijk af van die ideale lijn. Omdat we x als oorzaak en y als gevolg nemen is de afwijking van elk punt gelijk aan de lengte van de verticale blauwe lijnstukjes hiernaast. Hoe ver de gemeten y van de "best passende" y afligt.

Die lengtes heten de residuen. Het residu van punt i noemen we d_i.

Als je je GR de beste regressielijn laat uitrekenen, bepaalt hij ook alle residuen d_i.
Die kun je vinden bij 2nd LIST 7:RESID
Je kunt ze, als je dat leuk vindt, bijvoorbeeld in L₃ zetten door in te toetsen: 2nd LIST 7:RESID STO 2nd L3

Die residuen gaan we gebruiken om de "beste lijn" te vinden.

2. Kleinste Kwadraten.

De methode van de kleinste kwadraten zegt nu, dat voor de beste lijn geldt dat de som van "alle residuen in het kwadraat" minimaal moet zijn:

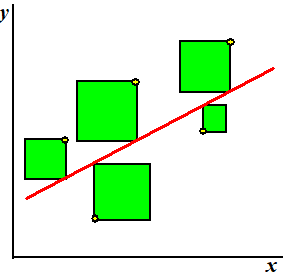
Het betekent eigenlijk dat je de rode lijn zó moet kiezen dat de totale oppervlakte van de groene vierkanten in de figuur hiernaast minimaal moet zijn. Dus afwijkingen verder van de lijn af tellen zwaarder mee dan afwijkingen in de buurt van de lijn.

Als we de regressielijn y = ax + b stellen, dan is de som van de kwadraten van de residuen minimaal als we kiezen:

Daarin is:

x̅ = x_gemiddeld en y̅ = y_gemiddeld Δx_i = x_i - x̅ en Δy_i = y_i - y̅

Het bewijs daarvan kun je hiernaast vinden. Twee verschillende bewijzen zelfs, wat wil je nog meer!
Dan móet het wel kloppen!!

Wat staat hier nou eigenlijk?

De vergelijking voor b is eenvoudig te interpreteren.
b = y̅ - ax̅ ⇒ y̅ = ax̅ + b
en daar staat niets anders dan dat het punt (x̅, y̅) op de regressielijn ligt.

De vergelijking voor a is lastiger te interpreteren.
De noemer komt je misschien nog bekend voor........????
Daar staat de totale kwadratische afwijking van alle x-en ten opzichte van het gemiddelde. Dat lijkt nogal op de standaarddeviatie σ_x, vind je niet? Die was gelijk aan de wortel van de gemiddelde kwadratische afwijking. Dus σ_x² (dat heette de variantie) is gelijk aan de gemiddelde kwadratische afwijking.
Als het aantal metingen gelijk is aan n, dan is de totale kwadratische afwijking gelijk aan n • σ_x² en dat is precies de noemer van de vergelijking voor a.

De teller is net zoiets, alleen dan niet de afwijkingen van x keer zichzelf, maar de afwijkingen van x keer de afwijkingen van y. Het is een soort "gecombineerde" variantie, en we noemen hem dan ook de Covariantie, en gebruiken er het symbool σ_xy en de afkorting Cov(x,y) voor:

(in deze les kun je er eventueel meer over lezen).

De teller van a is dus gelijk aan n • σ_xy,en omdat de noemer gelijk was aan n • σ_x² , kun je de vergelijking voor a ook heel kort en krachtig schrijven als:

Voorbeeld.

Stel op algebraïsche wijze een vergelijking van de regressielijn op die bij de volgende tabel hoort.

x	2	4	5	8	12	13	15
y	3	2	6	4	6	9	6

De gemiddelde x is 8,429 en de gemiddelde y is 5,143, dus het centrale punt is (8.429, 5.143)
Dat geeft de volgende tabel:

x	2	4	5	8	12	13	15
y	3	2	6	4	6	9	6	∑
Δx	-6,429	-4,429	-3,429	-0,429	3,571	4,571	6,571	-
Δy	-2,143	-3,143	0,857	-1,143	0,857	3,857	0,857	-
ΔxΔy	13,777	13,920	-2,939	-0,490	3,060	17,630	5,631	50,589
(Δx)²	41,332	19,616	11,758	0,184	12,752	20,894	43,178	149,714

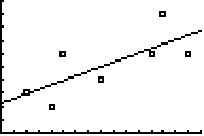
Dan is a = ^50,589/_149,714 ≈ 0,34 en b = 5,143 - 0,34 • 8,429 ≈ 2,24
De regressielijn heeft vergelijking y = 0,34x + 2,24
In de volgende tabel zie je hoe groot de voorspelde waarden van y zijn, en ook de residuen en hun kwadraat.
Tenslotte staat ernaast een puntenwolk met de regressielijn erin.

x	2	4	5	8	12	13	15
y	3	2	6	4	6	9	6	∑
0,34x + 2,24	2,97	3,65	3,99	5,01	6,37	6,71	7,39	-
residu d_i	-0,03	1,65	-4,01	1,01	0,37	-2,29	1,39	-
d_i²	0,0009	2,72	16,08	1,02	0,14	5,24	1,93	27,13

OPGAVEN

Stel op algebraïsche wijze een vergelijking op van de regressielijn die bij onderstaande gegevens hoort.

x	1	3	3	5	7
y	5	6	4	4	3

y = -0,37x + 5,79

Jolanda en Gerben hebben helaas nog nooit gehoord van regressielijnen. Zij proberen bij onderstaande puntenwolk op het oog zo goed mogelijk een rechte lijn erdoor te tekenen.
Jolanda tekent de lijn y = -0,7x + 8
Gerben tekent de lijn y = -0,5x + 7

Leg met behulp van een berekening van de residuen uit wie van beiden de beste lijn heeft getekend volgens de methode van de kleinste kwadraten.

J: Σd² = 9,17
G: Σd² = 17,25

Laat zien hoeveel verbetering er nog te halen is door de "echte" regressielijn te berekenen.

y = -0,8x +8,4
Σd² = 2,4

Een puntenwolk die symmetrisch is in een horizontale lijn of in een verticale lijn heeft een horizontale regressielijn. Leg duidelijk uit aan de hand van de formules voor de regressielijn waarom dat zo is.

Voor de covariantie s_xy wordt ook wel eens de volgende formule gegeven:

Toon aan dat deze formule klopt.

Gegeven is de volgende tabel met meetgegevens:

x	1	1	2	2	3	4	4	5	5	6	6	7	7	8	11
y	2.0	4.0	2.5	4.0	3.5	3.0	5.0	4.0	6.0	3.5	5.5	6.0	8.0	8.0	3.0

Geef een vergelijking van de regressielijn.

y = 0,31x + 3,05

Welk van de meetwaarden ligt het verst van de regressielijn af?
Welke d_i² heeft deze meetwaarde?
Hoe verandert de regressielijn als die meetwaarde niet wordt meegeteld, maar als meetfout wordt beschouwd?
Leg uit waarom de totale som van d² niet precies afneemt met d_i² als je zo'n punt i niet meer meetelt.

(11,3),
d_i² = 11,89
y= 0,64x +1,86

Wat is er met een puntenwolk aan de hand als alle d² even groot en niet nul zijn?