|
|
 |
|
Het regressie-effect. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
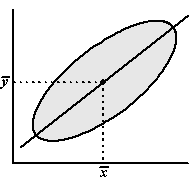
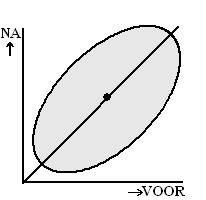
Laten we beginnen met een
geweldig onderzoek: een puntenwolk met zóveel punten dat we ze niet eens
allemaal kunnen tekenen, maar aangeven als één grijze ellips.
Hiernaast staat de centrale lijn van deze ellips getekend.
Dat is niet de regressielijn, maar de symmetrieas van de ellips.
Als je een regressielijn (van y op x) gaat tekenen
dan ga je ervan uit dat x de oorzaak is, en y het gevolg. |
 |
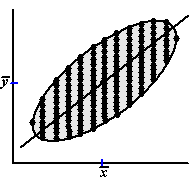
Dan kijk je dus bij één bepaalde
x welke y-waarden er allemaal gemeten zijn, en ga je de
lijn zó kiezen dat de som van de residuen in het kwadraat minimaal is.
Bij zo'n volledig symmetrische figuur als de ellips hiernaast zal het je
vast niet verbazen dat die ideale regressielijn gaat door de midden van
de verticale stippenlijnen hiernaast (er zijn er natuurlijk nog veel meer
dan hier getekend)
|
 |
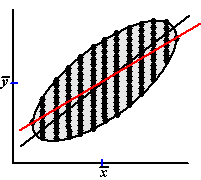
De regressielijn van y op x is
de rode lijn hiernaast. Hij gaat ook door het centrale punt, maar loopt
vlakker dan de centrale lijn (dat is aan de uiteinden het duidelijkst te
zien: de regressielijn gaat door die twee uiterste punten waar de
raaklijn aan de ellips verticaal is, terwijl de centrale lijn door de
toppen van de ellips gaat).
| |
| De regressielijn van y op x
loopt vlakker dan de centrale lijn |
|
| |
|
 |
Dit laatste effect heet het
regressie-effect.
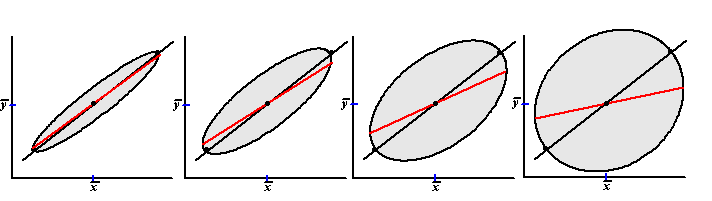
En hoe kleiner de correlatiecoëfficiënt r is, des te groter is dit
regressie-effect. Kijk maar naar de volgende plaatjes: |
| |
|
 |
| |
Van links naar rechts wordt de
correlatiecoëfficiënt r steeds kleiner maar het regressie-effect steeds
groter (dat is immers het verschil tussen de rode en de zwarte lijn).
Het VOOR-NA onderzoek!
Dit regressie-effect kom je het vaakst tegen bij een zogenaamd
voor-na onderzoek. Een bepaalde groep proefpersonen wordt getest op een
eigenschap voor een behandeling en na een
behandeling. Bijvoorbeeld: we onderzoeken de wiskundecijfers VOOR en NA
een examentraining, of we meten de bloeddruk VOOR en NA het gebruiken
van een medicijn, of noem maar op. |
Als je dan het resultaat van de eerste test
op de x-as zet, en dat van de tweede test op de y-as, dan
kun je een puntenwolk van je metingen maken. Laten we eens aannemen dat
er geen effect van de behandeling is. Dus dat de resultaten (gemiddelde
en spreiding) VOOR en NA gewoon gelijk zijn. Natuurlijk zal niet elk
proefpersoon precies dezelfde resultaten hebben, maar gemiddeld en qua
spreiding de hele groep wél. De centrale lijn zal de lijn y =
x zijn.
|
 |
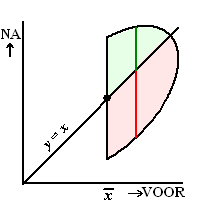
Maar bekijk nu eens alleen degenen met een
eerste score hoger dan het gemiddelde. Dat geeft de afgesneden ellips
hiernaast. De mensen in het rode gebied zullen op de tweede test een
lagere score halen, de mensen in het groene gebied een hogere score.
Maar dat rode gebied is veel groter.
Dat betekent dat de kans dat zo iemand bij de tweede test een lagere
score haalt dan op de eerste test groter is dan een hogere score. Het rode verticale lijntje
is langer dan het groene! |
 |
| En andersom zullen mensen die de eerste score
onder het gemiddelde zaten bij de tweede score juist vaker hoger scoren. |
|
Sir Francis Galton kwam dit
effect het eerst tegen toen hij de lengtes van vaders en zonen met
elkaar vergeleek. Daarbij viel op dat erg lange vaders gemiddeld minder
lange zonen kregen, en korte vaders juist gemiddeld langere zonen dan
zijzelf.
Hij noemde het effect "regression towards mediocrity". |
| |
|
| Je kunt het ook op de volgende
twee manieren zien: |
| |
|
| |
• |
De proefpersonen met eerst een erg lage waarde bestaan uit
twee soorten. Je hebt mensen die echt gewoon slecht zijn en
daarom laag scoren, maar je hebt ook mensen die wel beter zijn,
maar een toevallige uitschieter naar beneden hadden. De eerste
soort mensen zal de tweede keer wéér laag scoren, maar de tweede
soort zal gemiddeld hoger scoren dan de eerste keer. Dus zal het
gemiddelde van de beide soorten samen omhoog gaan. |
| |
|
|
| |
• |
Neem iets volkomen willekeurigs: laat een aantal personen 50
keer een muntstuk opgooien. Neem vervolgens degenen met minder
dan 25 keer KOP, en laat die nog een tweede serie worpen doen.
Het gemiddelde van die tweede serie is uiteraard 25 keer kop, en
dus hoger dan het eerste gemiddelde, want de eerste keer had
immers iedereen minder dan 25 keer kop? |
|
| |
|
| De
regressie-valkuil |
|
| |
|
Ik beweer dat ik een nieuwe
rekenmethode heb ontwikkeld, die vooral geschikt is voor
basisschoolleerlingen die zwak in rekenen zijn. Ik ga daarmee naar een
aantal basisscholen en vraag hen om deze methode één maand te laten
gebruiken door hun zwakste rekenleerlingen. Vooraf doen we een test wie
de zwaksten zijn, en na een maand doen we weer een test om te kijken of
mijn methode werkt.
Wedden dat er verbetering is???
Ik kan dan natuurlijk trots beweren wat voor geweldige methode ik heb
ontworpen.
Maar als je iets weet van het regressie-effect, dan trap je daar
natuurlijk niet zomaar in.
Als je de methode alleen toepast op degenen met in het begin de laagste
rekenscores dan zal dat een tweede keer statistisch gezien altijd een
hogere score geven, ook al gebeurt er niets! |
Toch wordt vaak trots opgeschept over zo'n methode, of zelfs beweerd dat
"wetenschappelijk is aangetoond" dat zo'n methode helpt. Je reinste
onzin natuurlijk! Gewoon het regressie-effect.
(De enige echt wetenschappelijke manier zou zijn om de
zwakste leerlingen willekeurig in twee groepen te verdelen, en dan de
ene groep de nieuwe methode laten volgen en de andere groep niet. Die
gebruiken we als testgroep. Dankzij het regressie-effect zullen beide
groepen er na afloop ongetwijfeld op vooruit zijn gegaan, maar nu valt
tenminste te meten of de ene groep het beter doet dan de andere) |
| |
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
Leg uit op welke manier het regressie-effect in
de volgende gevallen een rol zou kunnen spelen. |
| |
|
|
|
| |
a. |
De politie laat op een aantal
gevaarlijke kruispunten waarschuwingsborden neerhangen, en
constateert tevreden dat het aantal ongevallen na een maand
minder is geworden. De borden helpen kennelijk! |
| |
|
|
|
| |
b. |
Toen zijn keelpijn na twee dagen
steeds erger werd ging hij naar de gebedsgenezer. Die behandelde
hem, en inderdaad werd de keelpijn daarna minder. Zie je wel dat
het werkt! |
| |
|
|
|
| |
c. |
In Amerika gelooft men heilig in de
"Sports-Illustrated-Cover-Jinx" (de voorpagina-vloek!).
Met een atleet die de voorpagina van Sports-Illustrated haalt
gaat het vervolgens meestal bergafwaarts! |
| |
|
|
|
| |
d. |
Het Israëlische leger
hield ooit een test om het effect van straf en beloning op de
pilotentraining te meten. Sommige leerling-piloten werden
gestraft na een extreem slechte landing, en anderen werden
beloond na een hele goede landing. Degenen die beloond werden
deden het de volgende landing meestal slechter, maar degenen die
gestraft werden deden het daarna gemiddeld veel beter. De
conclusie was dat belonen slecht is, maar dat bestraffen helpt! |
| |
|
|
|
| |
e. |
uit The Star Online, 18 - 2 -
2003: |
|
| |
|
| |
|
KUALA LUMPUR:
Prime Minister Datuk Seri Dr Mahathir
Mohamad congratulated Malaysian shuttler Mohd Hafiz
Hashim for his achievement but warned that he should
not be "spoilt" with gifts like previous champions.
"Very
good and congratulations, but now I would like to
request everybody not to spoil him," he said when
asked to comment on Hafiz's victory in the men's
singles final of the All-England Badminton
Championships on Sunday.
Dr Mahathir said people should remember what had
happened to previous champions when they were spoilt
with gifts of land, money and other items.
"I hope
the states will not start giving acres of land and
money in the millions, because they all seem not to
be able to play badminton after that," he said after
taking part in the last dry run and dress rehearsal
for the 13th NAM Summit at the PWTC yesterday.
|
| |
|
| |
|
|
|
| 2. |
Van een groot aantal vader-dochter
koppels werd de lengte gemeten. De lengte van vader werd als
oorzaak gezien voor de lengte van dochter. Men vond voor de
vaders een gemiddelde lengte van 175 cm net een
standaarddeviatie van 16 cm. Voor de dochters vond men een
gemiddelde lengte van 164 cm met een standaarddeviatie van 14
cm.
De correlatiecoëfficiënt bleek gelijk te zijn aan 0,74. |
| |
|
|
|
| |
a. |
Geef een vergelijking van de regressielijn. |
|
| |
|
|
| |
b. |
Kees is 169 cm lang. Voorspel
de lengte van zijn dochter Tine. Bereken daarna hoeveel procent
beiden naar verwachting van het gemiddelde af zitten, en
verklaar het verschil tussen deze percentages. |
| |
|
y =
160,12
Δx = 3,4%,
Δy = 2,4%
|
|
| |
c. |
Jolande is 167 cm lang. Voorspel de
lengte van haar vader Tim. Bereken daarna hoeveel procent beiden
naar verwachting van het gemiddelde af zitten, en verklaar het
verschil tussen deze percentages. |
| |
|
|
x =
179.63
Δx = 2,6%,
Δy = 1,8%
|
|
| |
|
|
|
| 3. |
Leg duidelijk uit waarom het
regressie-effect groter is, als r dichter bij 0 ligt. |
| |
|
|
|
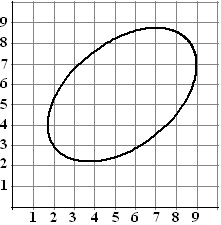
| 4. |
Hiernaast staat een
ellips die een puntenwolk zo goed mogelijk omsluit.
Bepaal met behulp van deze figuur zo goed mogelijk hoe groot
r
is. |
 |
| |
|
|
|
| |
|
| |
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|