spiegelen lineaire grafiek


Een rechte lijn spiegelen.	© h.hofstede (h.hofstede@hogeland.nl)

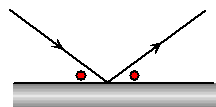
Uit de Natuurkunde is er een bekende wet (de wet van Snellius) die zegt dat als een lichtstraal weerkaatst, de hoek van inval gelijk is aan de hoek van weerkaatsing. In de tekening hiernaast betekent dat, dat beide rode hoeken gelijk zijn.

Hè Bah! Natuurkunde! Kunnen we niet gewoon terug naar Wiskunde?

Je hebt helemaal gelijk. Wiskunde is veel en veel leuker. Laten we dit onderwerp door een wiskundige bril bekijken.
Dan zien we meteen dat die lichtstralen natuurlijk gewoon rechte lijn van de vorm y = ax + b zijn.
Een interessante vraag is natuurlijk: "Wat gebeurt er met die a en b als zo'n lijn gespiegeld wordt?" Wat is het verband tussen de oorspronkelijke a en b en de nieuwe a en b na spiegelen?

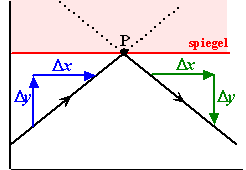
Hiernaast zie je een lijn die weerkaatst in een spiegel.
Wat daar vooral gebeurt is dat de helling van die lijn verandert. De helling in het begin is die blauwe ^Δy/_Δ_x de helling na afloop is die groene ^Δy/_Δ_x

Daar is een duidelijk verband tussen!

Ze zijn namelijk even groot. Er is maar één verschil; de eerste lijn stijgt en de tweede daalt. (in de figuur zie je dat Dy van de eerste lijn positief is, en van de tweede lijn negatief). Ofwel:

Bij spiegelen verandert de helling van teken.

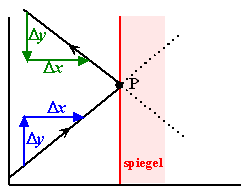
Hiernaast zie je dat bij spiegelen in een verticale spiegel precies hetzelfde gebeurt.
Wat er met b gebeurt is wat lastiger te zeggen. Die verandert wel natuurlijk, maar hoe dat precies gebeurt hangt van de plaats van het punt waar de lijn de spiegel raakt af.
Om de nieuwe b te berekenen kun je het beste dat "spiegelpunt P" invullen in de vergelijking y = ax + b (waarvan je a intussen al hebt)

b berekenen:
punt van spiegelen invullen!

Voorbeeld.
De lijn y = 2 + 3x (voor y < 14) spiegelt in de horizontale spiegel y = 14. Geef een vergelijking van de gespiegelde lijn.
Oplossing: De lijn was y = 2 + 3x dus de helling was 3. Dan wordt de nieuwe helling a = -3
y = 14 betekent 2 + 3x = 14 en dat geeft vrij eenvoudig x = 4. Het punt van spiegelen is dus (4,14)
De nieuwe lijn y = -3x + b moet door (4,14) gaan, dus 14 = -3 • 4 + b en dat geeft b = 26.
De gespiegelde lijn heeft vergelijking y = -3x + 26.

OPGAVEN

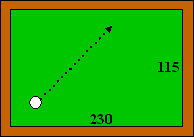
Het biljart hiernaast heeft binnenafmetingen (het groene deel) 230 cm bij 115 cm.
We kiezen de oorsprong van ons assenstelsel linksonder in de hoek.
Een witte bal ligt dan in het punt (40, 40) en wordt met een helling a = 0,9 weggestoten. Beschouw de bal als een punt.

Geef een vergelijking van de baan van deze bal na twee keer weerkaatsen.

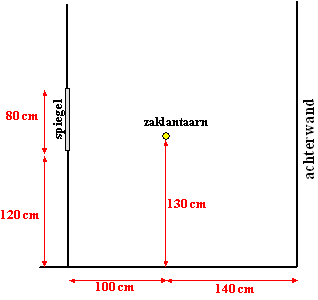
y = 0,9x - 288

Zie de figuur hiernaast.

Met een zaklantaarn wordt in een spiegel geschenen. Daardoor komt er op de achterwand een lichtvlek.

De afmetingen zijn als hiernaast.

Stel vergelijkingen voor de mogelijke lichtstralen op en bereken daarmee de hoogte van deze lichtvlek. Neem aan dat de achterwand oneindig hoog is.

272 cm