© h.hofstede (h.hofstede@hogeland.nl)

Boek I, propositie 44.
       

Gegeven een hoek, een lijnstuk AB en een driehoek,
dan kun je een parallellogram maken met zijde AB dat gelijk is aan die driehoek
en waar de gegeven hoek een hoek van is.
       
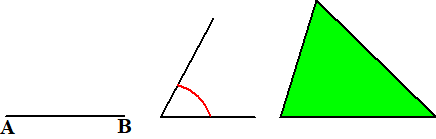
Begin met een driehoek een lijnstuk AB en een gegeven hoek..
       
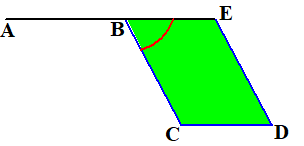
Maak een parallellogram, gelijk aan de gegeven driehoek, met zijde BE in het verlengde van AB, en met de gegeven hoek bij B. (I-42)

 
       
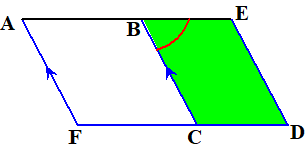
Teken AF parallel aan BC,   (I-31)
en verleng CD tot CF (P2).

       
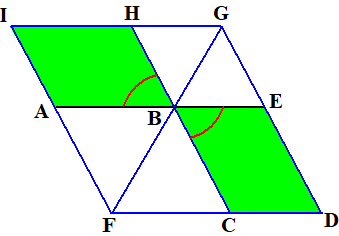
Verleng FB en verleng DE tot het snijpunt G. (P2)
Dat snijpunt is er zeker, want:
FC snijdt de parallellen AF en BC, dus de hoeken AFD en FDE zijn samen 180º  (I-29)
Dus de hoeken CFB en FDE zijn muinder dan 180º dus FB en DE snijden elkaar (P5)

Teken GI parallel aan AB   (I-31)
Verleng FA tot FI   (P2)
Verleng CB tot CH. (P2)

Het gezochte parallellogram is nu ABHI, want:

De oppervlakte van ABHI is gelijk aan de oppervlakte van CDEB en dat was de oppervlakte van de driehoek  (I-43)  (L1)

De rode hoeken zijn gelijk  (overstaande hoeken)
(I-15)

       

© h.hofstede (h.hofstede@hogeland.nl)