steekproef en populatie

© h.hofstede (h.hofstede@hogeland.nl)

Van populatie naar steekproef

Oké, de vorige les hebben we wat termen die bij steekproeven horen bekeken en ook wat manieren om steekproeven samen te stellen. Deze les gaat het over de grote en belangrijke vraag:

Hoe vind ik een eigenschap uit de populatie terug in mijn steekproef?

Daarvoor voeren we eerst twee termen in:

•

populatieproportie = P = het deel van de populatie dat een bepaalde eigenschap heeft.

Natuurlijk is die P onbekend (als hij bekend was, waarom zou je dan een steekproef of een onderzoek doen?)

•

steekproefproportie = p = het deel van mijn steekproef dat een bepaalde eigenschap heeft.

Deze les gaan we "van P naar p", dat wil zeggen: stel dat de populatieproportie gelijk is aan P, hoe zal dat invloed hebben op mijn (waarschijnlijk, verwachte) steekproefproportie p?
Dat is gelukkig vrij eenvoudig.

Het snoepautomaat-model

Zie de populatie als een enorme bak met snoepjes (nog vele keren groter dan die hiernaast) waaruit je willekeurig een handje (je steekproef) haalt. Die snoepjes hebben allemaal een bepaalde eigenschap (kleur). Bijvoorbeeld: Hoeveel zullen er geel zijn?

Stel nu dat een proportie P van de hele automaat geel is, hoe groot zal dan de proportie gele snoepjes in mijn steekproef van n snoepjes zijn?

Een aanname.
We nemen nu eerst even aan (later komen we daar nog op terug) dat onze snoepautomaat oneindig groot is. Als we er dan een handje van n snoepjes uithalen, maken we de aanname dat bij elk snoepje de kans dat het geel is P is, ook al is dit een trekking zonder terugleggen.

N.B.
In theorie is dat natuurlijk niet helemaal waar: stel dat er 200000 gele snoepjes en 800000 anderen in mijn snoepautomaat zitten. Dan is de kans dat het eerste snoepje geel is ²⁰⁰⁰⁰⁰/₈₀₀₀₀₀ = 0,25. Maar bij het tweede snoepje is er al een gele uit, dus is de kans dat de volgende wéér geel is gelijk aan ¹⁹⁹⁹⁹⁹/₇₉₉₉₉₉ = 0,2499990625 en dat is niet helemaal gelijk aan 0,25. Ik hoop dat je ziet dat bij grote aantallen (en niet al te grote steekproeven) deze aanname wel toegestaan is (dat ene gele snoepje maakt op die miljoen snoepjes niet zo veel verschil.....).

De oplossing.
Nou, als de kans elke keer weer P is, dan hebben we te maken met een binomiaal experiment!
n = onze steekproefgrootte
P = populatieproportie
En van binomiale experimenten kennen we al het gemiddelde en de standaarddeviatie (deze les) namelijk:

E = μ = n • P
σ = √(nP(1 - P))

Voorbeeldje.
Stel dat in de Verenigde Staten voor de komende presidentsverkiezingen tussen Hillary Clinton en Donald Trump 58% aanhanger van Clinton is en 39% aanhanger van Trump (en dus 3% geen mening heeft). Hoe groot is dan de kans dat er in jouw steekproef van 100 mensen minstens 62 Clinton-aanhangers zitten?

•

Nou simpel: n = 100, P = 0,58, P(X ≥ 62) = 1 - binomcdf(100, 0.58, 61) ≈ 0,2401

•

Je kunt deze kans natuurlijk ook eenvoudig met een normale verdeling benaderen:
μ = 58, σ = √(100 • 0,58 • 0,42) = 4,9356
De kans is dan normalcdf(61.5, ∞ , 58, 4.9356) = 0,2391
(Let op: die 61,5 in plaats van 62, die komt van de continuïteitscorrectie).

Conclusie:
Als je populatie groot genoeg is, dan zal het aantal successen in je steekproef bij benadering normaal verdeeld zijn met μ en σ als hierboven.

Kleine populaties.

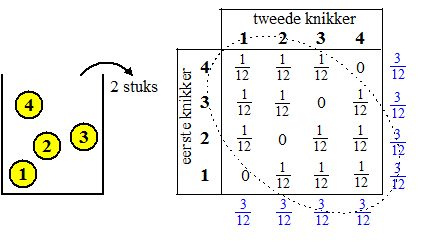
Bij kleine populaties is er natuurlijk wél een verschil tussen een steekproef met terugleggen en een steekproef zonder terugleggen. De kansen op de afzonderlijke successen zijn nu niet meer onafhankelijk, immers als er een exemplaar met een bepaalde eigenschap uit de steekproef is verdwenen is de kans op die eigenschap voor de volgenden kleiner geworden.

Laten we een erg kleine populatie nemen (Laat ik maar zeggen dat ik dat voor de duidelijkheid doe, maar in werkelijkheid doe ik het puur voor mezelf om me een boel rekenwerk te besparen). Neem een vaas met vier knikkers genummerd van 1 tm 4, en haal er twee uit. Deze keer dus ZONDER terug te leggen.

In de tabel zie je de erg eenvoudige gezamenlijke kansverdeling. Merk nog even op dat er bij trekking MET teruglegging overal in deze tabel ¹/₁₆ zou staan.

Het gemiddelde.

Eén ding valt wel op: die totale kansen (blauw aan de zijkant) zijn nog steeds allemaal ¹/₄ net als bij trekking met teruglegging. Dat is ook wel logisch natuurlijk: als je helemaal geen informatie over de eerste knikker hebt dan is de kans dat de tweede nummer 3 is even groot als de kans dat de eerste knikker nummer 3 is. Zonder kennis van knikker 1 heeft knikker 2 gewoon de populatieverdeling, immers vooraf is de kans dat de tweede knikker nummer 2 wordt ¹/₄, en nu is dat nog steeds zo.

vergelijkbaar:
Als je 10 mensen willekeurig uit een pak kaarten een kaart geeft, dan is vooraf de kans dat de eerste persoon ♠A krijgt natuurlijk even groot als de kans dat de achtste persoon ♠A krijgt, namelijk gewoon ¹/₅₂.

Dat heeft als gevolg dat de gemiddelde waarde van X gelijk is aan de waarde bij wel terugleggen.
Kortom E = μ = n • P blijft gewoon geldig.

de populatiegrootte heeft geen invloed op E

De standaarddeviatie.

Die is wel anders, immers als nummer 2 als eerste getrokken is, kan hij niet weer als tweede worden getrokken. Dat verklaart de nullen in de tabel hierboven. Maar daarin zie je ook al wel (door die beide nullen aan de zijkant) dat er een negatieve correlatie is tussen de eerste en de tweede knikker (de gestippelde ellips geeft dat ongeveer aan)
En dat is in het algemeen zo: als een eigenschap eenmaal al voorkomt in je steekproef, is de kans op die eigenschap daarna kleiner geworden, dus is er altijd een negatieve correlatie.
Voor de variantie van X₁ en X₂ geldt: Var(X₁ + X₂) = Var(X₁) + Var(X₂) + 2 • Cov(X₁, X₂) (deze les)
Dat betekent dat de variantie in het geval zonder terugleggen kleiner is dan in het geval met terugleggen, want Cov is negatief.

kleinere populaties geven een kleinere standaarddeviatie

Misschien helpt dit voorbeeldje:

Stel dat ik van de mensen in mijn woonwijk een steekproef van 10 neem om hun inkomen te bepalen. Als de eerste persoon nou toevallig die ene miljonair is die in mijn woonwijk woont, dan is dat wel erg toevallig en zal het gemiddelde inkomen wel te hoog uitvallen. Maar als ik die miljonair terugleg, dan zou ik hem zelfs NOG een keer kunnen trekken!! Dat zou een nog veel extremer antwoord geven. Dat zal in een trekking zonder terugleggen niet kunnen gebeuren. Vandaar dat trekkingen zonder terugleggen een betrouwbaarder (lees: kleinere variantie) gemiddelde opleveren.

Misschien helpt het niet...

Het blijkt dat de variantie in het aantal successen bij een steekproef van n exemplaren uit een populatie van N afneemt met een reductiefactor:

In ons geval van n = 2 uit N = 4 zou een factor ^{(4 - 2)}/_{(4
- 1)} = ²/₃ gelden voor de variantie van het aantal successen.
Meteen maar even checken dan?
Stel dat we in bovenstaand voorbeeld het aantal even knikkers tellen (succes = een even knikker)
ZONDER terugleggen geeft dat de volgende tabel:

aantal even	gebeurtenissen	kans
0	13, 31	²/₁₂
1	12, 21, 14, 41, 23, 32, 34, 43	⁸/₁₂
2	24, 22	²/₁₂

Mijn GR gaf E = 1 en σ = √(¹/₃) en dus Var = ¹/₃

MET terugleggen geeft dat de volgende tabel:

aantal even	gebeurtenissen	kans
0	13, 31, 11, 33	⁴/₁₆
1	12, 21, 14, 41, 23, 32, 34, 43	⁸/₁₆
2	24, 22, 22, 44	⁴/₁₆

Mijn GR gaf E = 1 en σ = √(¹/₂) en dus Var = ¹/₂

Het KLOPT: Factor ²/₃

OPGAVEN

Stel je neemt een steekproef door een dobbelsteen 1000 keer te gooien. Als die steen zuiver is, dan verwacht je natuurlijk zo ongeveer een gemiddelde van 3,5.
Bereken de kans dat het gevonden steekproefgemiddelde (bij een zuivere dobbelsteen) méér dan 0,1 afwijkt van de verwachte 3,5.

0,064

Een accountant telt 200 bedragen bij elkaar op, maar rond elk bedrag af op de dichtstbijzijnde 10 cent.
Neem aan dat de eindcijfers van de oorspronkelijke bedragen willekeurig verdeeld zijn.
Hoe groot is de kans dat zijn uiteindelijke antwoord meer dan 1 euro van de werkelijke waarde afligt?

0,0138

Bij het spel bridge kent men punten toe aan de verschillende kaarten volgende de volgende tabel:

kaart	puntenwaarde
A H V B de rest	4 3 2 1 0

Een bridgespeler krijgt van de 52 kaarten er 13 in zijn hand.
Wat is het gemiddelde en wat is de standaarddeviatie van het totaal aantal punten dat hij krijgt?

10 en 4,13

Een lift is ontworpen met voor maximale belasting van 1000 kg. Stel dat er 10 mensen in de lift stappen en dat die mensen komen uit een populatie met een gemiddelde gewicht van 93 kg met een standaarddeviatie van 10 kg.

Bereken de kans dat het totale gewicht van de mensen meer dan 1000 kg is, als de mensen uit een oneindig grote populatie komen.

0,0134

Bereken de kans dat het totale gewicht van de mensen meer dan 1000 kg is als de mensen uit een populatie van in totaal 500 mensen komen.

0,0127