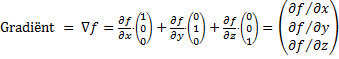© h.hofstede (h.hofstede@hogeland.nl)

Partiële differentiaalvergelijkingen.
       
Het woord zegt het al:  partiële differentiaalvergelijkingen zijn vergelijkingen waarin partiële afgeleiden staan, dus die gaan over functies van meerdere variabelen. Hoe dat precies werkt met partiële afgeleiden staat in deze les, en dat moet je eerst maar lezen eigenlijk.
Deze les eerst wat termen en notatiemanieren voordat we "echt" beginnen.

Operatoren.

Een operator is net zoiets als een functie, alleen het is een functie.....voor een functie!
Kijk, een functie "doet iets" met een getal; het verandert een getal namelijk via één of ander voorschrift in een ander getal. Nou een operator doet ook iets, maar niet met een getal, maar met een functie. Dus een operator verandert een functie via één of ander voorschrift in een andere functie. Een operator geven we meestal aan met de letter L  (ik weet ook niet waarom, maar dat doet iedereen zo).
       

Een operator L verandert een functie in een andere functie.
       
Voorbeelden van operatoren:
L(f ) = d/dx(f ) = f '   de afgeleide van f nemen.
L(f ) = - f    omgekeerde van f nemen:  de grafiek van f spiegelen in de x-as.
L(f ) = ∫f dx    de primitieve van f nemen.
L(f) = ∂/∂t (f) = ∂f/∂t   de partiële afgeleide  van  f  naar de tijd nemen.    
L(f ) = ∂²/∂x²(f ) = ∂²(f)/∂x²  de tweede partiële afgeleide van f naar de variabele  x nemen.
       
Lineaire operatoren.

Dat zijn operatoren die voldoen aan:

L(c1 • f1 + c2 • f2) = c1 • L(f1) + c2 • L(f2)
       
Een lineaire vergelijking is dan een vergelijking met een lineaire operator. Die ziet er dus uit als  L(f) = g   waarbij L die lineaire operator is.

Een lineaire partiële differentiaalvergelijking   is dan een vergelijking met een lineaire operator waarin partiële afgeleiden voorkomen, maar dat had je waarschijnlijk zelf ook al wel geraden.

Een lineaire homogene partiële differentiaalvergelijking  is dan een vergelijking met een lineaire operator L waarin partiële afgeleiden voorkomen, maar die er bovendien uitziet als  L(f) = 0 (dus met g = 0). Voor zulke homogene vergelijkingen is altijd f = 0 een oplossing (bewijsje van één regel:  neem twee willekeurige oplossingen, dan is elke lineaire combinatie c1f1 + c2f2 ook een oplossing, dus ook die met met c1 = c2 = 0.  q.e.d.)
Vaak is het een handige test om even snel te kijken of een vergelijking homogeen is, door te proberen of  f = 0 een oplossing is. Als dat niet zo is, is 'íe ook niet homogeen!
       
Randvoorwaarden en Beginvoorwaarden.

Veel van de differentiaalvergelijkingen (bijna allemaal eigenlijk) komen uit de natuurkunde of scheikunde, en daar bekijken we meestal functies die afhangen van de plaats en de tijd. In het algemeen is dan  f = f(x, y, z, t)  waarbij t de tijd aangeeft    en  x, y en z de plaats (bij tweedimensionale problemen alleen x en y en bij ééndimensionale problemen alleen x).

De voorwaarden voor x, y en z noemen we dan  randvoorwaarden, en die voor t heten beginvoorwaarden.
Randvoorwaarden zien er uit als  f(x0, y0, z0, t) = g(t)  en die omschrijven hoe de functie er op elk tijdstip op plaats
(x0, y0, z0) uit moet zien.
Beginvoorwaarden zien er uit als  f (x, y, z, t0) = g(x, y, z) en die omschrijven hoe de functie er overal uitziet op tijstip t0. 
       
Beroemde 3D-operatoren

Er zijn een paar operatoren die je in veel partiële differentiaalvergelijkingen tegenkomt. Voornamelijk vergelijkingen uit de natuurkunde trouwens.

De allerbelangrijkste is de gradiënt.  Dat is eigenlijk een soort "ruimtelijk afgeleide"  van een functie f(x, y, z)
De gradiënt zegt hoe een functie varieert (wat de helling is) in de x-richting en in de y-richting en in de z-richting.
Er is zelfs een speciaal teken voor verzonnen:  ∇
De gradiënt verandert een functie in een vector met drie kentallen:
       

       
De tweede operator die vaak voorkomt is de divergentie. Die telt de afgeleides van een ruimtelijke functie f in de drie basisrichtingen bij elkaar op.  Geeft dan één waarde;  een soort van "gemiddelde afgeleide"
       

       
Kijk vooral naar die ene stip:  daardoor staat hier een inproduct en komt er één waarde uit! Geen vector!!
       
De derde operator die ik toch echt even moet noemen is de Laplace-operator. Dat is eigenlijk een divergentie, maar dan voor de tweede afgeleides.
       

       
       
1. Leg van onderstaande partiële differentiaalvergelijkingen uit welke operator L is gebruikt, en ook welke vergelijkingen lineair en welke homogeen zijn.
       
  a. ∂f/∂t = c • ∂²f/∂x² + f 2 
       
  b. ∂f/∂t = k • ∂²f/∂x² + 2x
       
  c.  ∂²f/∂x² =   ∂²f/∂y² - 2 • ∂²f/∂z²
       
  d. ∂f/∂t  +  c • ∂²f/∂x²   =  2f - 2x2  + ∂²f/∂t²   
       
  e.  ∂²f/∂t²   =  ∂f/∂t • ∂f/∂x + f 
       
     

© h.hofstede (h.hofstede@hogeland.nl)