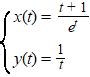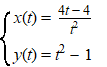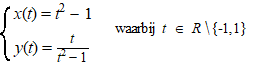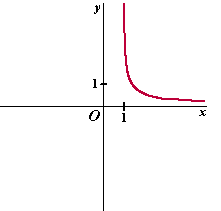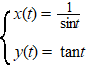© h.hofstede (h.hofstede@hogeland.nl)
Asymptoten bij parameterkrommen.
   
Ik hoop dat je nog weet hoe je bij gewone functies asymptoten moest onderzoeken. Anders even een snel mini-geheugenopfrisser:

•  Verticale asymptoten:  als x naar een bepaalde waarde gaat, gaat y naar  ±∞
•  Horizontale asymptoten:  als x naar  ±∞  gaat,  gaat y naar een bepaalde waarde.
•  Scheve asymptoten:  als x naar ±∞ gaat, gaat de helling  y' naar een bepaalde waarde.

Zo, dat was het. Korter kan haast niet.

Maar bij parameterkrommen is de zaak wat anders:  er is een vergelijking voor x(t) en een vergelijking voor y(t) en die leveren sámen een kromme op.

Zulke asymptoten zouden in de volgende gevallen kunnen voorkomen:
   
1.  verticale asymptoten.
Bekijk de waarden van t  waarvoor y naar oneindig gaat. Als x dan naar een constante waarde gaat, dan is er een verticale asymptoot. Dat zou dus ook heel goed kunnen bij t die ±∞  wordt.

2.  horizontale asymptoten.
Bekijk de waarden van t waarvoor x naar oneindig gaat. Als y dan naar een constante waarde gaat, dan is er een horizontale asymptoot. Dat zou dus ook heel goed kunnen bij t die ±∞  wordt.

Merk op dat deze twee regels bijna hetzelfde zijn! Dat moet natuurlijk ook wel, want bij parameterkrommen is er eigenlijk geen verschil tussen x en y.  Ze worden op dezelfde manier behandeld. Als je de x(t) en y(t) formules verwisselt, is het enige wat er gebeurt dat de kromme gespiegeld wordt.

3.  scheve asymptoten.
Bekijk of er een t-waarde is waarvoor x en y beiden naar ±∞  gaan. Als die er is, onderzoek dan of de helling  y'/x' constant wordt voor die t-waarde. Dat zou dus ook heel goed kunnen bij t die ±∞  wordt.
   
Voorbeeld 1.  
Er zijn geen constante t-waarden waarvoor x of y naar oneindig gaan.
Blijft over de mogelijkheid dat t naar ±∞ gaat.

Als t naar ∞ gaat, dan gaan y en x beiden naar ∞.  Dat zou een scheve asymptoot kunnen zijn, maar de helling y´/x´ gaat dan ook naar ∞ (ga dat zelf maar na). Dus die scheve asymptoot is er niet.

Als t naar -∞ gaat, dan gaat x naar -∞ en y naar nul. Dat betekent dat de kromme een verticale asymptoot y = 0 heeft
   
Voorbeeld 2.  
 
t naar ±∞  is nu niet zo interessant; dan gaan x en y beiden naar nul.

Dus moet je maar eens kijken wat er gebeurt als t naar -1 toegaat, want dan worden beide noemers nul, dus gaan zowel x als y naar oneindig. Dan wordt het interessant wat y'/x' doet....
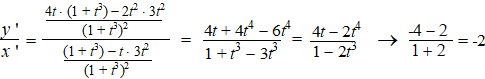De helling gaat naar -2, dus dat is een scheve asymptoot y = -2x + b
Dat betekent dat y + 2x naar b nadert als t naar -1 gaat:
(om de noemer in de tweede stap te ontbinden heb ik een staartdeling gemaakt)
De scheve asymptoot is blijkbaar de lijn y = -2x - 2/3.
   
       
  OPGAVEN
       
1. Kromme K is gegeven door:   x(t) = t • et + 2  en  y(t) = t2 • et + 2
       
  a. Welke waarden kunnen x en y aannemen?
       
  b. Bereken de coördinaten van de snijpunten van K met de assen.
       
  c. Bereken de coördinaten van K met een horizontale of verticale raaklijn.
       
  d. Onderzoek of  K asymptoten heeft. Bekijk óók scheve asymptoten.
       
2. Kromme K is gegeven door:
 

       
  a. Onderzoek welke waarden x en y kunnen aannemen.
       
  b. Onderzoek of K horizontale of verticale asymptoten heeft.
       
3.
  Daarin geldt 0 ≤ t  ≤ 2π
       
  a. Welke waarden kunnen x en y aannemen?
       
  b. Bereken de coördinaten van de snijpunten van K met de assen.
       
  c. Geef de vergelijkingen van de asymptoten van K
       
  d. Toon aan dat  4 + x2y2 = 4x2  een vergelijking is van K
       
4. examenvraagstuk VWO Wiskunde B, 1987.

Ten opzichte van een rechthoekig assenstelsel Oxy is de kromme K voor t ∈ R\{0}gegeven door:
       
 

       
  a. Bereken de coördinaten van het punt van K waarin de raaklijn aan K evenwijdig is aan de y-as.
Stel een vergelijking op van de raaklijn in O aan K.
       
  b. De lijn met vergelijking x = -3 snijdt K in de punten A en B.  Bereken AB.
       
  c. Stel van elk van de asymptoten van K een vergelijking op.
       
5. examenvraagstuk VWO Wiskunde B, 1987.

Ten opzichte van een rechthoekig assenstelsel Oxy is de kromme K gegeven door:
x = 1/4t2 - 3t  en  y =  t + 4/t - 5,  waarbij  t ∈ R.
       
  a. Bereken de snijpunten van K en de coördinaatassen.
       
  b. Onderzoek of K een asymptoot heeft.
       
  c. Bereken in graden nauwkeurig de hoek van K en de y-as.
Bereken de coördinaten van de punten van K waarin de raaklijn aan K evenwijdig is aan de x-as of aan de y-as.
       
  d. Bewijs dat K zichzelf snijdt in het punt (-1,7)
       
6. examenvraagstuk VWO Wiskunde B, 1988.

Ten opzichte van een rechthoekig assenstelsel Oxy  is de kromme K gegeven door:
 
  Stel van elke asymptoot van K een vergelijking op.
       
7. examenvraagstuk VWO Wiskunde B, 1989.

Ten opzichte van een rechthoekig assenstelsel Oxy is de kromme K gegeven door:
x = ln | t  |  en  y = t2 - 4t  waarbij  t ∈ R\{0}

       
  a. Bereken de coördinaten van de snijpunten van K en de coördinaatassen.
       
  b. Stel een vergelijking op van de asymptoot van K.
       
  c. Bereken de coördinaten van het punt van K waarin de raaklijn aan K evenwijdig is aan de x-as.
       
8. examenvraagstuk VWO Wiskunde B, 1990.

Ten opzichte van een rechthoekig assenstelsel Oxy is voor   t ∈ R\[0, 1/2] de kromme K gegeven door:
x = ln(2t2 - t)  en   y = t2 + 2t
       
  a. Bereken de coördinaten van de snijpunten van K met de coördinaatassen.
       
  b. Bereken de coördinaten van het punt van K waarin de raaklijn aan K evenwijdig is aan de x-as.
       
  c. Stel van elke asymptoot van K een vergelijking op.
       
9. examenvraagstuk VWO Wiskunde B, 1993.

Ten opzichte van een assenstelsel Oxy is de kromme K gegeven door:
x =  ln | t + 1 |  en   y = ln | t - 1 |  waarbij  t ≠ -1  en   t ≠ 1.

Er zijn drie snijpunten van K met de coördinaatassen.
       
  a. Bereken de richtingscoëfficiënten van de raaklijnen in deze snijpunten.
       
  K heeft een horizontale, een verticale en een scheve asymptoot.
       
  b. Stel een vergelijking op van elk van deze asymptoten.
       
10. examenvraagstuk VWO Wiskunde B, 1995.
       
  De kromme K, voor een gedeelte getekend in de figuur hiernaast, is gegeven door:

 
  Waarbij  t  ∈ 〈0, 2π〉 \ {1/2π, π, 11/2π}.
De asymptoten van K zijn evenwijdig aan de coördinaatassen.

Stel een vergelijking op van de asymptoten van K. Geef een toelichting.
       
     

© h.hofstede (h.hofstede@hogeland.nl)