Laten we een bekende figuur nemen: een
kegel.
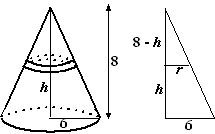
We nemen er eentje met hoogte 8 en straal van grondvlak 6.
Als we daar de oppervlakte van willen uitrekenen dan kunnen we hem in
allemaal ringetjes snijden met hoogte dh en straal r
Als je zo'n ringetje "uitvouwt" krijg je (ongeveer)
een rechthoek (niet helemaal: de zijkanten lopen heel ietsje scheef
maar als die ringetjes maar dun genoeg zijn, dan kun je dat wel
verwaarlozen.
De lengte van zo'n rechthoekje is 2πr,
de breedte noemen we voorlopig dB
Maar in de rechterfiguur hiernaast zie je dat (8-h)/r
= 8/6
Daaruit volgt 6(8 - h) = 8r ⇒ 48
- 6h
= 8r ⇒ r = 6 - 0,75h
|
 |
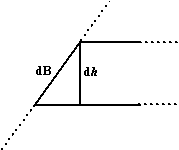
Kunnen we de breedte dB van zo'n ringetje ook uitdrukken in h?
Hiernaast zie je een detailtekening. Die schuine lijn dB heeft dezelfde
helling als de rand van de kegel in het vooraanzicht, en die heeft
lengte 10 (Pythagoras)
Dus uit gelijkvormigheid geldt: 8/10
= dh/dB
Dus dB = 1,25dh
Dan wordt de oppervlakte van zo'n strookje gelijk aan 2π(6
- 0,75h)•1,25dh
Voor de som van al die ringetjes moet je uiteraard een integraal opstellen: |
 |
|
|
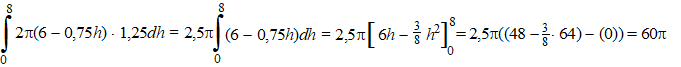 |
| |
|
| De algemene aanpak is dus: |
|
|
Verdeel de oppervlakte op een symmetrische manier in
stroken met dikte dx
Schrijf de oppervlakte van één zo'n strook op
Maak een integraal om al die stroken bij elkaar op te tellen. |
|
| |
|
|
Werkt dat ook bij gebogen
oppervlakten? |
| |
|
Jazeker, alleen zit je een beetje
met die dB. Die is dan "krom".
Neem het stuk van de grafiek y = √x tussen x = 0 en x
= 4. Als je dat om de x-as wentelt krijg je een zogenaamde "paraboloïde"
zoals hiernaast geschetst.
Een schijfje heeft in deze figuur omtrek 2πh
= 2π√x
De breedte is dB
In het figuurtje onderaan zie je dat dat de lengte van de grafiek van
y(x) is.
Maar daar hebben we in een eerdere les al een formule voor afgeleid!!!
|
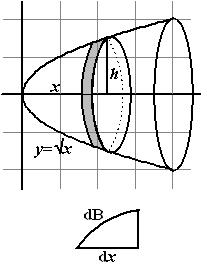 |
| Dat geeft voor de oppervlakte van
de paraboloïde: |
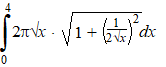 |
Nou ja, je kunt hem vast nog wel
vereenvoudigen, maar ik denk dat ik de primitieve toch niet kan vinden.
Ziet er veel te moeilijk uit. Dit lijkt me typisch een taak voor mijn
GR!
Invoeren bij Y1= en dan calc - integraal geeft mij een
oppervlakte van ongeveer 46,1. |
| |
|
| Voor degenen die van formules
houden, we hebben eigenlijk dit gedaan: |
|
|
|
oppervlakte van een
omwentelingslichaam om de x-as: |
|
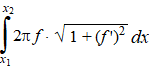 |
|
|
| |
|
|
OPGAVEN |
|
|
| 1. |
De oppervlakte van een bol. |
| |
Benader door een integraal uit te
rekenen de oppervlakte van een bol met straal 6. |
|
|
|
|
|
|
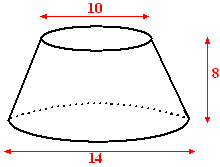
| 2. |
Bereken de oppervlakte
van de lampenkap hiernaast met behulp van een integraal. |
|
|
|
|
|
|
|
| 3. |
Gegeven is de
functie f(x)
= 2 - √x
met domein [0,4]
Je kunt de grafiek van f om de x-as wentelen, maar ook om de y-as. |
|
|
|
| a. |
Onderzoek hoeveel de inhouden van de
omwentelingslichamen die je dan krijgt van elkaar
verschillen |
| |
|
| b. |
Bereken door zelf
een integraal op te stellen de buitenoppervlakte van het
omwentelingslichaam dat ontstaat bij wentelen om de x-as.
Geef je antwoord in twee decimalen nauwkeurig. |
|
|
|
|
|
|
|
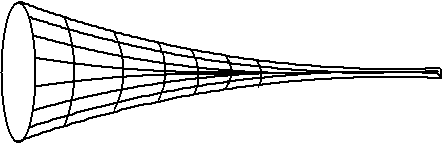
| 4. |
Gabriëls trompet. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hierboven staat een
omwentelingslichaam dat je kunt krijgen door de grafiek van y
= 1/x van x = 1 tot x
= oneindig te wentelen om de x-as. |
|
|
|
|
|
|
|
a. |
Toon aan dat de inhoud van deze
trompet gelijk is aan
π. |
| |
|
|
|
b. |
Beredeneer door een integraal op te
stellen dat de oppervlakte van deze
trompet oneindig groot is. |
| |
|
|
| |
c. |
Huh? Een figuur met eindige
inhoud maar oneindige oppervlakte?
Dus alle verf die je er in giet is niet genoeg om de oppervlakte
te verven? Terwijl het toch ook overal tegen de binnenkant aan
zit! Hoe kan dat? |
| |
|
|
| 5. |
Gegeven
is het parabooldeel y = 4x - x2
met domein [0,4]
Dit parabooldeel wordt gewenteld om de x-as.
Bereken de oppervlakte van het lichaam dat je dan krijgt. Doe dat door zelf een
integraal op te stellen.
Geef je antwoord in twee decimalen nauwkeurig. |
| |
|
| |
|
|
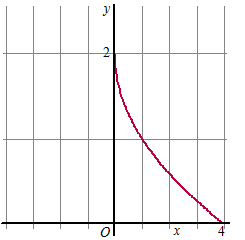
| 6. |
De grafiek
van y = 2 - √x
voor 0 < x < 4 wordt gewenteld om de y-as.
Bereken de oppervlakte van het omwentelingslichaam dat zo
ontstaat. |
 |
| |
|
|
| |
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|