series opeenvolgende getallen


Series opeenvolgende getallen.	© h.hofstede (h.hofstede@hogeland.nl)

Deze les draait eigenlijk om het volgende raadsel:

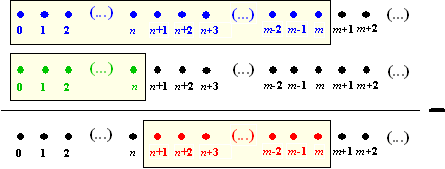
Wiskundig vertaald staat daar:
Als je de som S van een aantal opeenvolgende getallen weet, kun je dan die getallen vinden?
Pluk een aantal getallen van de getallenlijn, bijvoorbeeld de roden hieronder:

Dan kun je die getallen in die rechthoek krijgen door alle getallen tot en met m te nemen en dan weer alle getallen tot en met n er af te trekken. Dus:

BLAUW min GROEN is ROOD = S

Maar er geldt 1 + 2 + 3 + ... + n = ¹/₂n(n+ 1)

Dat is de som van een rekenkundige reeks en uitleg daarover kun je hier vinden.
Met deze formule kun je dat blauwe en dat groene deel makkelijk omschrijven:

S = ¹/₂m(m + 1) - ¹/₂n(n + 1)

Dat gaan we uitdrukken in m:
S = ¹/₂m²+ ¹/₂m - ¹/₂n² - ¹/₂n ⇒ m² + m - n² - n - 2S = 0
Daar staat een ABC-formule voor m met a = 1 en b = 1 en c = (-n² - n - 2S)

Daar kan alleen een geheel getal (m) uitkomen als dat stuk onder die wortel precies een kwadraat is, en dan ook nog van een oneven getal (anders wordt het met dat delen door twee niet geheel).
Dus er moet een getal p (oneven) bestaan zodat p² = 1 + 4n² + 4n + 8S.

Maar....daar staat weer een ABC-formule, nu voor n. Kijk maar: 4n² + 4n + (1 + 8S - p²) = 0, en dat geeft:

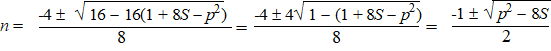Er geldt weer hetzelfde: als n een geheel getal moet zijn, dan moet dat stuk onder die wortel weer een kwadraat zijn, en dan ook nog van een oneven getal. Dus er moet een getal q (oneven) bestaan zodat q² = p² - 8S
q² = p² - 8S ⇒ 8S = p² - q² = (p - q)(p + q)
daarin zijn q en p beiden oneven, dus p - q en p + q zijn beiden even.

Wat staat hier? Het getal 8S is ontbonden in twee even factoren. Als je die twee (q - p en q+ p) kunt vinden, dan kun je daarmee p en q vinden. Als die beiden ook oneven zijn, dan kun je n vinden en daarna ook m. En als je n en m hebt, dan weet je ook welke serie opeenvolgende getallen je moet nemen om S te krijgen (namelijk van n + 1 tot en met m)

Voorbeeld. Schrijf S = 26 als de som van opeenvolgende gehele getallen.
8S = 8 • 26 = 208.
208 ontbinden geeft 1 • 208 en 2 • 104 en 4 • 52 en 8 • 26 en 13 • 16
in aanmerking komen de gevallen met beiden even: 2 • 104 en 4 • 52 en 8 • 26.
2 • 104 geeft p = 53 en q = 51 en die zijn beiden oneven. Dat geeft n = 25 en m = 26 en de nogal saaie serie "26"
4 • 52 geeft p = 28 en die is even, dus dat kan niet.
8 • 26 geeft p = 17 en q = 9 en die zijn beiden oneven. Dat geeft n = 4 en m = 8 en de serie "5 + 6 + 7 + 8 = 26"

Schrijf 1000 op twee mogelijke manieren als som van opeenvolgende getallen (1000 zelf telt niet).

55 + 56 + ... + 70
198 + ...+202

Schrijf 500 op drie mogelijke manieren als som van opeenvolgende getallen (500 zelf telt niet).

8 + 9 + ... + 32
59 + ...+ 66
98 + ...+ 102

Als je voor het ontbinden van 8S kiest voor 8S = 2 • 4S, dan krijg je uiteindelijk als "serie" het getal S zelf.
Toon dat aan .