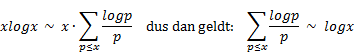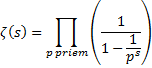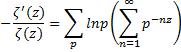© h.hofstede (h.hofstede@hogeland.nl)

Nulpunten van de zetafunctie
       
Dit was de functionaalvergelijking waarmee Riemann de zetafunctie naar het hele complexe vlak uitbreidde:
       

       
Aan die functionaalvergelijking kun je direct zien dat ζ(s) nul wordt als  s = -2, -4, -6, ....

Waarom dat zo is?

Nou, omdat dan  sin(ps/2) nul is natuurlijk.  Dûh!  
Nou ja...  ook omdat  Γ(1 - s) en  ζ(1 - s) beiden niet oneindig groot worden, want 1 - s is in die gevallen positief. 

Over s = 0 kun je bijvoorbeeld niet zomaar iets zeggen:  dan is de sinus nul, maar de  ζ(1 - s) = ζ(1) = ∞
De nulpunten -2, -4, -6, .....  noemen we daarom heel toepasselijk de triviale nulpunten.

Een belangrijke vraag is:  "Zijn er nog meer nulpunten?"

Voordat je denkt:  "Nou ja zeg, ik heb mijn tijd wel beter te besteden", zal ik proberen uit te leggen waarom dat in onze getaltheorie best een belangrijke vraag is.

Hoeveel priemgetallen zijn er eigenlijk?

Priemgetallen zijn voor wiskundigen erg belangrijk. 

Elk bestaand getal kun je namelijk beschouwen als opgebouwd uit priemgetallen, immers elk getal kun je schrijven als een vermenigvuldiging van priemgetallen.

 
priemgetallen zijn de bouwstenen van alle andere getallen!
 

't Is eigenlijk net als in de scheikunde. Daar is elke stof een molecuul (wat in de wiskunde een getal is). Maar elk molecuul is opgebouwd uit atomen (dat zijn de wiskundige priemgetallen).  Net zoals je scheikundig "Water" kunt schrijven als H2O  zou je wiskundig het getal 45 kunnen schrijven als 325. 
En zwavelzuur (H2SO4) lijkt dan misschien wel wat op het getal 39375 (= 32754). 
Oké ik geef het toe;  het is niet helemaal precies hetzelfde, want er zijn maar een beperkt aantal atomen, en er zijn oneindig veel priemgetallen.

Daarom is wiskunde ook zoveel interessanter dan scheikunde natuurlijk...maar dat wist je natuurlijk al wel.

Nou zijn er dan wel oneindig veel priemgetallen (al door Euclides bewezen) maar de vraag is:  "Hóe oneindig?" 

Laten we de functie  թ(n)  bekijken die aangeeft hoeveel priemgetallen er tot en met het getal n bestaan (in de literatuur wordt deze functie meestal  π(n) genoemd, maar ik vind dat π uniek moet blijven, dus heb ik er maar een ander teken voor genomen)
       

թ(n) = aantal priemgetallen  ≤  n

       
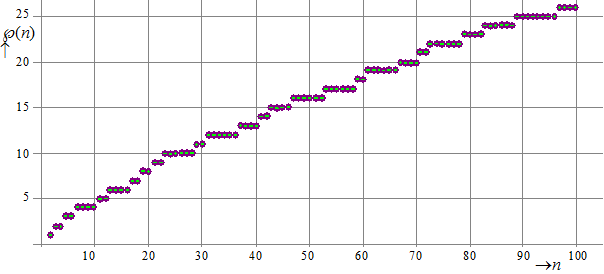
Hieronder zie je de grafiek voor de eerste honderd waarden van n.
       

       
Daar is best een soort grafiek in te onderscheiden, waarbij natuurlijk onmiddellijk de vraag rijst:  welke functie hoort bij deze grafiek? 
Gauss en Legendre losten dat probleem beiden en onafhankelijk van elkaar ongeveer op, zo rond 1800. Ze vonden beiden dat deze grafiek steeds meer gaat lijken op de grafiek van  y = x/logx.  Preciezer wiskundig geformuleerd:
       

       
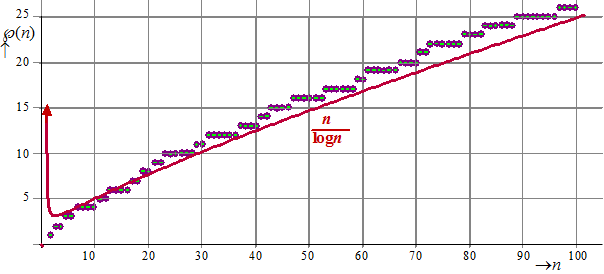
Om eerlijk te zijn... onze twee helden hadden het niet helemaal goed....

Legendre dacht dat de waarde van deze limiet naar ongeveer 1,08366 ging. Gauss durfde zich er niet over uit te laten....
Hieronder zie je de grafiek van y = n/logn bij de priemaantallen getekend.
       

       
Een nogal slordige aanpak...

Pas in 1852 kwam Tschebychef met een soort van aannemelijkmakerij waarom deze grafiek inderdaad թ(n) zou benaderen.
Zijn aanpak ging ongeveer als volgt:
       
  Laten we eens kijken hoe vaak een bepaalde priemfactor p voorkomt in n!
Neem bijvoorbeeld  10! = 10 • 9 • 8 • 7 • 6 • 5 • 4 • 3 • 2 • 1  en laten we eens gaan beredeneren hoe vaak de priemfactor 2 daarin voorkomt.  We introduceren daarvoor eerst de notatie  [ x ]  en daarmee bedoelen we:  het getal x naar beneden op een geheel getal afgerond.

Oké:  hoe vaak komt 2 voor?
• in alle even getallen minstens één keer.  Dat is al  [10/2] = 5 keer   (van de getallen  10, 8, 6, 4, 2)
• in de 22 = viervouden  minstens twee keer, dus dat is al  [10/4] = 2 keer extra  (van de getallen 4, 8)
• in de 23 = achtvouden  minstens drie keer, dus dat is weer  [10/8] = 1 keer extra  (van het getal 8)
• in de hogere machten van 2 niet meer, want 24 is al meer dan 10
In totaal komt de priemfactor 2 dus  5 + 2 + 1 = 7 keer in 10! voor.

In het algemeen komt de priemfactor p  precies   [x/p] + [x/p²] + [x/p³] + ......  keer voor in x!

Maar  x!  is natuurlijk gelijk aan het product van alle priemfactoren die erin voorkomen:
 

  Neem de log van beide kanten en bedenk dat  logxn = nlogx .  Dat geeft:
 

  Maar volgens de formule van Stirling is logx!  ongeveer gelijk aan xlogx
Verder is  voor grote waarden van x de waarde van  [x/p]  ongeveer gelijk aan x/p  en zijn die termen  [x/p²] + [x/p³] + ......  te verwaarlozen ten opzichte van die eerste term  [x/p].
Dat geeft dan samen:
 

  Dat kriebeltje  ~  betekent:  "....is van de orde van grootte van.....". In het verhaal erboven staat immers een paar keer  "is ongeveer gelijk aan" en ook "is te verwaarlozen" , dus zo heel precies is 't allemaal niet.
   
   
Een beetje nettere aanpak....

Euler liet op zijn geweldige manier (deze les) zien dat ζ verbonden is met het aantal priemgetallen, door de volgende formule te ontwikkelen:
 

   
We gaan nu proberen om van deze uitdrukking over te stappen naar het aantal priemgetallen (թ).

Allereerst gaan we deze functie differentiëren. Omdat daar een product staat moeten we de productregel gebruiken.
Er staat  f(p1) • f(p2) • f(p3) • f(p4)....  met  f(p) = (1 - p-s)-1
Met de productregel geeft dat:  
f '(p1) • {f(p2) • f(p3) • f(p4)....}   +   f '(p2) • {f(p1) • f(p3) • f(p4)....}  +   f '(p3) • { f(p1) • f(p2) • f(p4)....} + ....
Daarbij is  f '(p) = -(1 - p-s)-2 • -p-s lnp • -1
Samen geeft dat:

Maar als we dat laatste product vermenigvuldigen met  (1 - p-s) / (1 - p-s),  dus eigenlijk de factor van priemgetal p weer toevoegen, dan staat daar precies weer  ζ(s):

Als je nu  ζ(s) naar de andere kant brengt, dan heb je een resultaat dat de moeite waard is te onthouden voor later:
 

   
1.  Alwéér een nieuwe functie:  ψ(x)

We definiëren eerst "zomaar" de nieuwe functie:
 

   
Daar moet natuurlijk wat toelichting bij......niemand snapt zomaar wat die m is.... 
De som gaat over alle priemgetallen kleiner dan x
Die mp(x) is de hoogste macht  (m van macht)  tot waar je het priemgetal kunt nemen als je nog kleiner dan x wilt blijven.
 
  Voorbeeldje tussendoor.
Neem x = 20
De priemgetallen kleiner dan 20 zijn  2, 3, 5, 7, 11, 13, 17, 19
Tot welke macht kun je ze nemen om onder de 20 te blijven?  (dat is m)
24 en  32  en de rest tot de macht 1.
Dus  ψ(20) = 4ln2 + 2ln3 + ln5 + ln7 + ln11 + ln13 + ln17 + ln19 » 6,6039

(zie je trouwens al, dat dat met het samennemen van die logaritmen ook gelijk is aan   ln(24 • 32 • 5 • 7 • 11 • 13 • 17 • 19) ???)
       
Heb je door dat het wel een beetje lijkt op dat gerommel van Tsjebycheff hierboven?
Als pm  <  x  dan is  ln(pm) < lnx  dus  m • lnp < lnx  dus  m < lnx/lnp
Maar omdat m het grootste gehele getal is waarvoor dat geldt, is  m = [lnx/lnp]   (zelfde notatie als hierboven)

OK. We gaan nu een verband tussen onze nieuwe  ψ(x) en de eerder gevonden waarde van  ζ '(s)/ζ(s)  aantonen.

We waren gebleven bij:
 

       
Maar als je die lnp weglaat dan staat daar gewoon de som van een meetkundige reeks! (met reden p-s)
Dit is dus een meetkundige reeks vermenigvuldigd met lnp:
       

       
Je moet nu sommeren over p én over n.
       
       
rest volgt...    
 

       
       
       
       
       
       
       
       
       
       
       

© h.hofstede (h.hofstede@hogeland.nl)