formule van Stirling


	© h.hofstede (h.hofstede@hogeland.nl)

De formule van Stirling.

In deze les is het de bedoeling om een idee te krijgen van hoe groot n! nou eigenlijk wordt als n heel groot wordt.
Hoe snel gaat dat???

Laten we gaan proberen om boven- en ondergrenzen voor n! te vinden.

Bovengrens.
Een bovengrens is vrij makkelijk te vinden
n! = n(n - 1)(n - 2) .....1 < n • n • n ..... = nⁿ
Dat betekent dat ln(n!) < ln(nⁿ) = nln()n

Ondergrens.
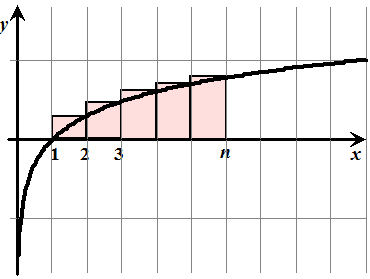
Dat is ietsje lastiger, maar als je de oppervlakte onder de grafiek van grafiek van logx bekijkt, dan kom je misschien op een idee. Misschien ook niet, daarom zal ik even helpen.

De oppervlaktes van die rode rechthoekjes hiernaast zijn samen gelijk aan ln2 + ln3 + .... + ln(n)
Maar je ziet dat ze samen meer zijn dan de oppervlakte onder de grafiek van lnx tussen 1 en n

Maar die oppervlakte kun je met een integraal uitrekenen:

ln(n!) = ln1 + ln2 + ln3 + ... + ln(n) < nln(n) - n + 1

Voorlopige conclusie:

nln(n) - n + 1 < ln(n!) < nln(n)

Deel nu deze ongelijkheid door nlogn: dan krijg je 1 - ¹/_ln(n) + ¹/_nln(n) < ^ln(n!)/_nln(n) < 1
Als n naar oneindig gaat, dan gaat ook de linkerkant naar 1.
Dat betekent dat ln(n!) ≈ n ln(n)

ln(n!) ≈ n ln(n)

Stirling kon het nóg beter!

Eerst even wat voorbereidend werk:

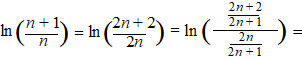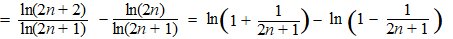Maar voor ln(1 + x) is er een reeksontwikkeling:

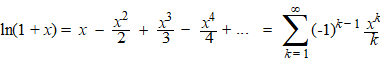Laten we die toepassen op deze beide ln-vormen:

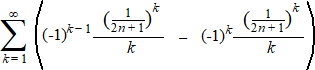Als k-1 een even getal is, dan heffen die twee delen elkaar op. Als k - 1 oneven is, dan versterken ze elkaar juist.
Dus we houden alleen nog de som over voor k = 1, 3, 5, ..... en dan dubbel zo groot.

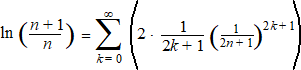Daarmee is het voorbereidende werk klaar.

We definiëren nu het volgende:

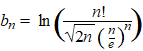De redenen daarvoor zullen straks blijken.
Spannend hé?

Dan geldt:

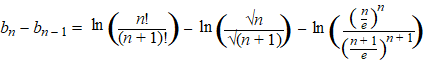term voor term vereenvoudigen:

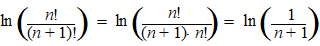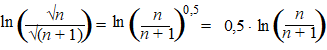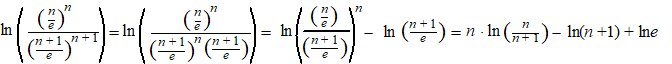En nu weer samenvoegen:

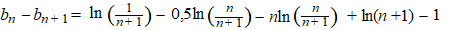De eerste en vierde term vallen tegen elkaar weg want ln(¹/_x) = ln(x^-1) = -lnx
De tweede en derde term kun je samennemen, dan blijft over:

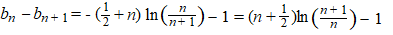Vergelijk dit met de reeksontwikkeling voor ln(^{(n + 1)}/_n) van bovenaan.

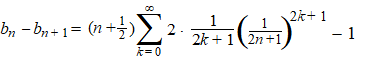Maar als je k = 0 neemt, dan komt er uit dat eerste deel precies 1, en die valt weg tegen die 1 daar achteraan.
Dus kun je net zo goed de som van k = 1 naar ∞ nemen en die -1 weglaten.
Verder wordt die 2(n + ¹/₂) precies gelijk aan 2n + 1 en valt weg tegen één van die uit de noemer. Dus de macht wordt eentje lager: 2k ipv 2k + 1:

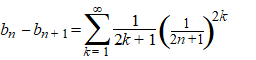Dat is groter dan nul, dus ons eerste resultaat is dat b_n > b_{n + 1}

b_n is een dalende rij

Maar omdat ¹/_{(2k + 1)} kleiner dan 1 is, wordt de som groter als je die factor weglaat:

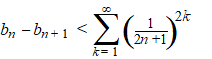Daar staat nu precies de som van een meetkundige rij.

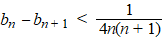Bekijk nu b₁ - b_n:
(b₁ - b_n) = (b₁ - b₂) + (b₂ - b₃) + (b₃ - b₄) + .... + (b_{n
- 1} - b_n) (zoiets heet een telescooprij)

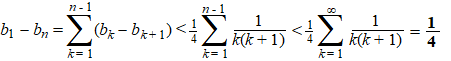Dat betekent dat b_n > b₁ - ¹/₄
Dat betekent dat b_n een ondergrens heeft.
We hebben dus te maken met een dalende rij die niet onder een bepaalde ondergrens komt.
Dat nadert dus naar een constante waarde.

Maar als b_n naar een constante waarde nadert, dan nadert ook e^bn naar een constante waarde.
Noem die waarde a, dan geldt kennelijk:

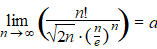Naar welke waarde a nadert dan?

Daarvoor hebben we eerst een beroemde formule van Wallis nodig:

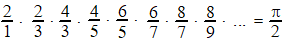Het bewijs daarvan staat hiernaast.

Laten we die per twee breuken ordenen:

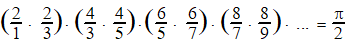Het aantal factoren tussen haakjes noemen we n. (Dus in het voorbeeld staan er n = 4 factoren)
We gaan nu teller en noemer vermenigvuldigen met (2 • 2)(4 • 4)(6 • 6)(8 • 8) • ..... (evenveel factoren)
Dat geeft:

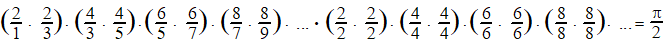De teller:
Haal van elk getal in de teller een factor 2 buiten haakjes. Dat zijn 2n • 2 = 4n factoren 2.
dan blijft over: (1 • 1)•(2 • 2)• (3 • 3) • (4 • 4) • ... • (1 • 1)•(2 • 2)• (3 • 3) • (4 • 4) • .... = (n!)⁴
Dus de teller is gelijk aan 2⁴ⁿ • (n!)⁴

De noemer.
Daar staat nu: 1 • 2 • 2 • 3 • 3 • 4 • 4 • 5 • 5 • 6 • 6 • 7 • 7 • 8 • 8 • 9 = ((2n)!)² • (2n + 1)
(die laatste (2n + 1) dat is in dit geval die 9)

Vervangen:

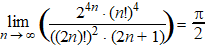Maar hierboven zagen we dat voor n naar oneindig geldt:

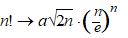Weer vervangen dan maar:

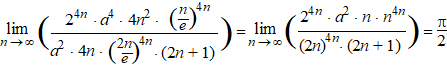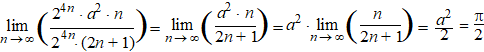Oké, dus a = √π

Dat geeft dan eindelijk de formule van Stirling: