| |
 |
|
De normaalvector van een vlak. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
Tot nu toe hebben we erg veel
zitten te prutsen met de richtingen van een vlak. Om de richting van een
vlak aan te geven hadden we twee richtingsvectoren nodig.
Dat kan makkelijker!!!
Je kunt de richting van een vlak ook met één vector aangeven! Denk na!
Welke vector bepaalt nou helemaal in één keer de richting van een vlak?
|
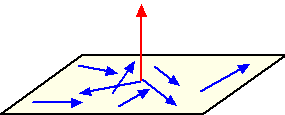 |
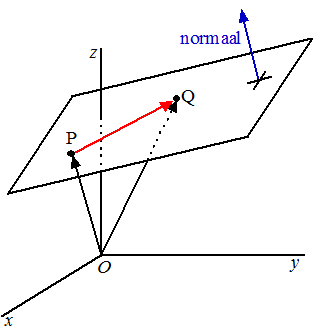
Natuurlijk; dat is de
vector die er loodrecht op staat!!! De
normaalvector dus....
Die ene rode vector in de figuur hiernaast zegt eigenlijk evenveel over
de richting van het vlak als al die blauwen bij elkaar.... |
| |
|
|
|
Het bepalen van de normaalvector.
Voor het bepalen van de normaalvector van een vlak is het erg belangrijk
dat je je beseft dat hij loodrecht staat op ALLE richtingen van het
vlak. Voor het bepalen van het loodrecht op elkaar staan of niet van
vectoren hadden we een aardige test. Weet je hem nog? Deze test: |
| |
|
|
|
|
twee vectoren staan loodrecht op elkaar
als hun inproduct nul is |
|
| |
|
|
|
 |
Dan is het niet
zomaar makkelijk te zien welke normaalvector met beiden inproduct nul maakt.
Daarom gaan we nieuwe richtingsvectoren maken, deze keer met nullen
erin!
Ik hoop dat je nog weet dat elke combinatie van twee richtingsvectoren
weer een richtingsvector is.
Nou, als je tweemaal die tweede vector neemt, en dat optelt bij de
eerste, dan krijg je dus weer een richtingsvector. Maar wel eentje met
een NUL erin!! |
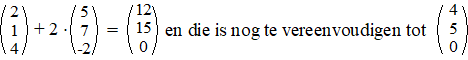 |
| Nou we eenmaal een
NUL hebben is het vinden van de normaalvector makkelijk. |
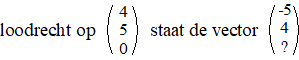 |
Waarbij dat
vraagteken dus nog alles mag zijn, immers dat vermenigvuldig je voor het
inproduct toch met NUL.
Maar we weten dat de normaalvector ook nog loodrecht op een andere
richtingsvector van het vlak moet staan: |
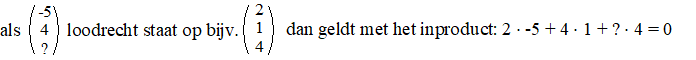 |
Daaruit volgt
-10 + 4 + 4 • ? = 0 ⇒ 4 • ? = 6
⇒ ? = 1,5
De kentallen van de normaalvector zijn dus -5 en 4 en 1,5.
Als je een hekel aan breuken hebt zou je er nog -10, 8 en 3 van
kunnen maken. |
| |
|
|
|
|
Normaalvector en vergelijking. |
| |
|
|
|
Bij lijnen
tweedimensionaal bleek dat de kentallen van de normaalvector in de
vergelijking ax + by = c stonden. Dat blijkt 3D ook
zo te zijn. We zullen dat eens op een andere manier bekijken.
Stel dat de steunvector van een vlak OP is, en dat Q een willekeurig
ander punt van het vlak is. Als P het punt (x0, y0,
z0) is en Q een willekeurig punt (x, y,
z) dan is de vector PQ gelijk aan: |
 |
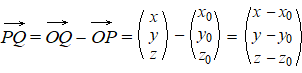 |
Maar omdat die vector
in het vlak ligt staat hij loodrecht op de normaalvector. En dat
betekent weer dat het inproduct van deze vector met de normaalvector nul
is.
Stel dat de normaalvector de kentallen a, b, c heeft, dan geeft
dat: |
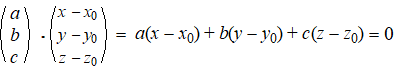 |
⇒
ax - ax0 + by -
by0 + cz - cz0 = 0
⇒ ax + by + cz =
ax0 + by0 + cz0
⇒ ax + by + cz =
d
die d is gewoon weer een nieuwe constante. En
daar heb je het al: de kentallen van de normaalvector zijn de
getallen uit de vergelijking. Precies wat we al verwachtten. |
|
|
|
De kentallen van de
normaalvector staan in de vergelijking |
|
|
|
Voorbeeld.
Een vergelijking van een vlak is 2x - 6y + 3z
= 12. Geef een vectorvoorstelling. |
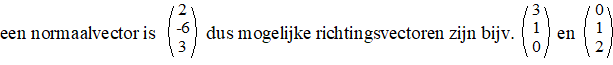 |
Die twee zijn zo
gekozen dat ze met de normaalvector inproduct nul geven.
Kies als steunvector een willekeurig punt van het vlak, bijvoorbeeld
(0, 0, 4), dan krijg je de vectorvoorstelling: |
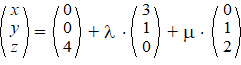 |
| |
|
|
|
| Voorbeeld. |
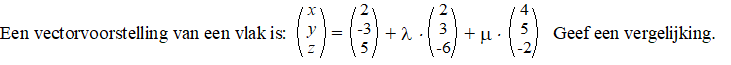 |
| Probeer eerst een nul
te fabriceren met die richtingsvectoren. Bijvoorbeeld twee keer de
eerste min de tweede. |
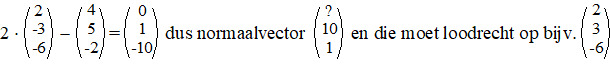 |
Dat geeft 2 • ?
+ 3 • 10 - 6 • 1 = 0 dus ? = -12, en de normaalvector heeft
kentallen -12, 10 en 1.
Een vergelijking is dan -12x + 10y + z = d
Vul de steunvector in, en je vindt d = -49. De gezochte
vergelijking is -12x + 10y + z = -49 |
| |
|
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
| 1. |
Geef een vectorvoorstelling van de
volgende vlakken: |
| |
|
|
|
|
| |
a. |
-3x + 5y -
6z = 20 |
| |
|
|
|
|
| |
b. |
x + 7y - 4z =
12 |
|
|
| |
|
|
|
|
| |
c. |
3x - 5z = 18 |
|
|
| |
|
|
|
|
| 2. |
Geef een vergelijking
van de volgende vlakken: |
| |
|
|
|
|
| |
a. |
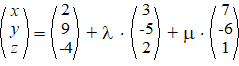 |
| |
|
|
|
|
| |
b. |
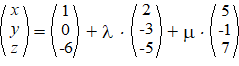 |
| |
|
|
|
|
| |
c. |
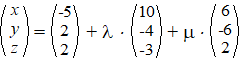 |
| |
|
|
|
|
| 3. |
Onderzoek of de volgende
lijnen loodrecht op de volgende vlakken staan. |
| |
|
|
|
|
| |
a. |
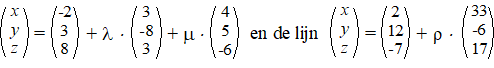 |
| |
|
|
|
|
| |
b. |
Vlak 2x - 3y
+ 6z = 12 en de lijn door (3, 5, 8) en
(-3, 14, 8) |
| |
|
|
|
|
| |
|
|
|
|
| 4. |
Gegeven zijn de punten
O(0,0,0) en A(6,3,0) en B(0,6,3) en C(0,3,6)
P is de projectie van O op vlak ABC.
Toon aan dat P op lijn AC ligt. |
| |
|
|
|
|
| 5. |
Bereken a en b zó dat
de vlakken 2x - y + 2z + 6 = 0
en ax + by - 4z = 0 evenwijdig
zijn.
Bereken vervolgens de afstand tussen beide vlakken. |
| |
|
|
|
|
| 6. |
Gegeven zijn de punten P(6, 1, 0) en
Q(4, 1, -2)
Geef een vectorvoorstelling van de verzameling van alle punten
die gelijke afstand tot P en Q hebben. |
| |
|
|
|
|
| |
|
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |