|
|||||
| 1. | a. |
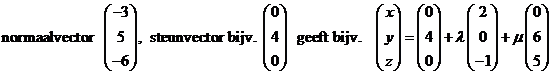 |
|||
| b. |
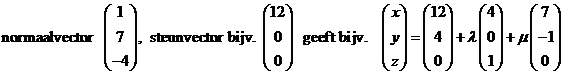 |
||||
| c. |
|
||||
| 2. | a. |
|
|||
| vergelijking 7x + 11y + 17z = 45 | |||||
| b. |
|
||||
| vergelijking -2z + y + z = -8 | |||||
| c. |
|
||||
| vergelijking 2x + 5y = 0 | |||||
| 3. | a. | inproducten: 33 • 3 - 6 • -8 + 17 • 3 = 198 33 • 4 - 6 • 5 - 17 • 6 = 0 niet beiden nul, dus niet loodrecht. |
|||
| b. |
|
||||
| Dat is niet dezelfde richting, dus niet loodrecht. | |||||
| 4. |
|
||||
|
|
|||||
| ABC is het vlak
x + y + z = 9 Punt (λ,λ,λ) invullen: 3λ = 9, dus λ = 3 en P is het punt (3, 3, 3) |
|||||
|
|
|||||
| Neem μ = 3 en je vindt inderdaad punt P. | |||||
| 5. |
|
||||
| Dat is zo als
a = -4 en b = 2 (0, 0, 0) ligt op het tweede vlak. Lijn door (0, 0, 0) loodrecht op het eerste vlak: |
|||||
|
|
|||||
| Punt (2λ, -λ,
2λ) invullen in het eerste vlak geeft 4λ +
λ + 4λ + 6 = 0 dus
λ = -2/3 De projectie van O op het vlak is P = (-4/3, 2/3, -4/3) OP = √(16/9 + 4/9 + 16/9) = 2 en dat is de afstand tussen beide vlakken. |
|||||
| 6. | Het is het
middelloodvlak van PQ. MPQ = (5, 1, -1) |
||||
|
|
|||||
| Dat is de
normaalvector van het vlak, dus het vlak heeft vergelijking -2x -
2z = a Punt M invullen geeft -10+ 2 = a dus het vlak is -2x - 2z = -8 ofwel 2x + 2z = 8 |
|||||