| |
 |
|
De Normaalvector. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
De normaalvector
van een gegeven vector is degene die er loodrecht op staat. Je snapt wel
dat er voor zo'n normaalvector een heleboel mogelijkheden zijn, immers
de lengte is onbelangrijk. Elke vector die loodrecht op een bepaalde
vector staat is daar een normaalvector van. Het enige dat je weet is dat
al die mogelijke normaalvectoren van een vector evenwijdig aan elkaar
zijn. Daarom zal ik het voortaan wat nauwkeuriger hebben over "een"
normaalvector.
De kentallen van een
normaalvector. |
| |
|
|
|
Hiernaast zie je een rode vector
met kentallen a en b waarvan een blauwe normaalvector is
getekend (let weer op het woordje "een"; de vector kan natuurlijk ook
langer of korter of de andere kant op gekozen worden, dan is íe nog
steeds loodrecht op de rode).
Laten we eerst voor het gemak die blauwe normaalvector precies even lang
tekenen als de oorspronkelijke rode vector. |
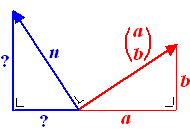 |
| Er zijn in die figuur
een aantal gelijke hoeken te vinden..... |
|
|
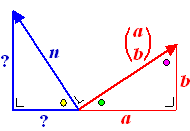
De bodemlijn is een rechte lijn, dus zijn die drie hoeken bij het begin
van de vectoren samen 180º. Maar omdat de vectoren loodrecht op elkaar
staan zijn de groene plus de gele hoek samen 90º.
Maar de groene hoek plus de paarse hoek zijn ook samen 90º want ze
vormen samen met een rechte hoek de drie hoeken van een driehoek.
Dus is de paarse hoek gelijk aan de gele. |
 |
Dan hebben die twee driehoeken twee gelijke hoeken (namelijk 90º en een
paarse/gele hoek). Dus zijn alle hoeken gelijk, dus ze zijn
gelijkvormig. Sterker nog; als de twee vectoren even lang zijn, dan zijn
de driehoeken dus precies hetzelfde (congruent heet dat). |
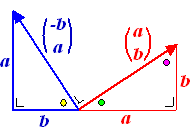
Dan kennen we die
twee blauwe vraagtekens ook: het zijn weer a en b.
De normaalvector heeft dezelfde kentallen als de oorspronkelijke, alleen
zijn de x en de y omgewisseld, en bovendien gaat de x
naar links in plaats van naar rechts, dus die is negatief. |
 |
| |
|
|
|
| |
|
|
|
| Die normaalvector kun
je langer of korter maken door de kentallen met een getal groter of
kleiner dan 1 te vermenigvuldigen. Je kunt hem ook de andere kant op
laten gaan door de kentallen met een negatief getal te vermenigvuldigen.
Alles mag; het geeft allemaal mogelijke normaalvectoren. |
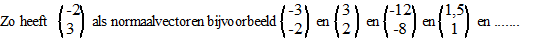 |
| Letterlijk teveel om
op te noemen. Als ik jou was zou ik (als ik mocht kiezen uit al die
normaalvectoren) de eenvoudigste kiezen (die tweede lijkt mij in
dit geval het simpelst). |
| |
|
|
|
|
De normaalvergelijking van een lijn. |
| |
|
|
|
Als klein
tussendoortje gaan we eerst even de vergelijking van een lijn op alweer
een andere manier schrijven.
Ik beweer dat je elke rechte lijn kunt schrijven als ax + by =
c.
Dat gaat mij wel lukken, kijk maar: |
| • |
y = 4x
- 3 ⇒ -4x + y
= -3 dus a = -4 en b = 1 en
c = -3 |
| • |
y = -1/3x
+ 2 ⇒ 1/3x
+ y = 2 dus a = 1/3
en b = 1 en c = 2 |
| • |
y = -1/3x
+ 2 ⇒ 3y = -x + 6
⇒ x + 3y = 6
dus a = 1 en b = 3 en
c = 6 en die is eigenlijk nog mooier...vind ik |
|
• |
y = 1
-
5/7x
⇒
7y = 7 - 5x
⇒ 5x + 7y = 7
dus a = 5 en b = 7 en c = 7 |
| |
|
|
|
Je ziet
dat er zelfs meerdere (oneindig veel!) mogelijkheden zijn. Ikzelf kies
graag degenen met gehele getallen. Ik heb nou eenmaal wat met gehele
getallen.
Andersom kun je ax + by = c als je dat wilt
weer omwerken naar de "oude vertrouwde" vergelijking die je gewend bent.
Kijk maar: |
| • |
4x + 2y
= 5 ⇒ 2y = -4x
+ 5 ⇒
y = -2x + 21/2. |
| • |
x
- 3y
= 12 ⇒ -3y = -x +
12 ⇒ y =
1/3x
- 4 |
| |
|
|
|
Die nieuwe vorm ax
+ by = c heet de normaalvergelijking
van een lijn.
Die normaalvergelijking vind ik eigenlijk nog mooier dan die oude y
= ax + b van vroeger.
Waarom?
Nou, in die vergelijking staan x en y wat symmetrischer,
en ik hou nou eenmaal van symmetrie.
Bovendien is er zelfs een soort lijnen die je wel met een
normaalvergelijking maar niet met y = ax + b kunt
beschrijven!!
Zie jij welke lijnen dat zijn?
Nou????? (antwoord staat in het zwarte blok
hiernaast, maar DENK EERST NA) |
| |
|
|
|
| Zo, dat was inderdaad
een kort tussendoortje, nu terug naar de normaalvectoren. |
| |
|
Een prettige eigenschap van
normaalvectoren. |
| |
|
|
|
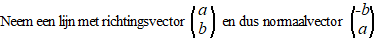 |
Die richtingsvector betekent dat je
bij a naar rechts ook b omhoog gaat. Dus bij
Δx = a hoort
Δy = b
Dan is de richtingscoëfficiënt gelijk aan
Δy/Δx
= b/a
Dus is de vergelijking van de lijn y = b/a
• x + p met p een constante.
Omwerken geeft: y = b/a
• x + p ⇒
ay = bx + pa
⇒ -bx + ay = pa
Maar die laatste pa is natuurlijk gewoon weer een
andere constante, dus die mogen we ook wel c noemen.
Dan staat er -bx + ay = c
Hé! Wakker worden!
Daar staat een normaalvergelijking!
En niet zomaar eentje: de getallen bij x en y zijn precies de
kentallen van de normaalvector!!! -b en a.....
Nou ja zeg.... Dát is handig.....!!! En nog makkelijk te onthouden ook:
|
| |
|
|
|
|
in de normaalvergelijking staan de
kentallen van de normaalvector. |
|
| |
|
|
|
| Kijk hoe handig dat
is: |
| |
|
|
|
| Voorbeeld
1. |
| Geef een
vectorvoorstelling van de lijn 3x - 2y = 6 |
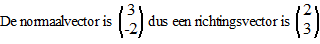 |
| Kies als steunvector
een willekeurig punt van de lijn, bijvoorbeeld (2, 0) |
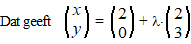 |
| |
|
|
|
| Voorbeeld
2. |
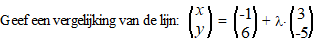 |
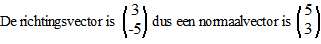 |
De vergelijking is
dus 5x + 3y = c en als je de steunvector
(punt (-1,6)) invult geeft dat c = 13
De vergelijking is dus 5x + 3y = 13. |
| |
|
|
|
| Voorbeeld
3. De raaklijn aan een cirkel. |
De raaklijn aan een
cirkel heeft de leuke eigenschap dat hij loodrecht staat op de lijn van
het middelpunt naar het raakpunt.
Loodrecht?
Dat vraagt om een normaalvector.
Neem een cirkel met middelpunt de oorsprong en straal 13. Dan gaat die
cirkel door het punt R = (5, 12). Toon dat zelf maar aan met
Pythagoras |
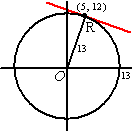 |
Als je een
vergelijking van de raaklijn in (5, 12) aan de cirkel wilt opstellen,
dan weet je dat OR daar loodrecht op staat dus dat is de normaalvector,
dus de kentallen van OR staan in de vergelijking.
De vergelijking is dan 5x + 12y = c
Vul punt R(5, 12) in en je vindt c = 5 • 5 + 12 • 12 = 169 en
de vergelijking is 5x + 12y = 169. |
| |
|
|
|
|
OPGAVEN |
| |
|
| 1. |
Geef vectorvoorstellingen van de
volgende lijnen: |
| |
|
|
|
|
| |
a. |
3x + 2y = -2 |
d. |
2y + 6x - 5 = 0 |
| |
|
|
|
|
| |
b. |
y = 1/2x
+ 8 |
e. |
4y - x = 12 |
| |
|
|
|
|
| |
c. |
y = -3x - 6 |
f. |
-2x = 3y - 4 |
| |
|
|
|
|
| 2. |
Geef vergelijkingen van de volgende
lijnen. |
| |
|
|
|
|
| |
a. |
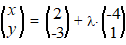 |
| |
|
|
|
|
| |
b. |
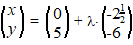 |
| |
|
|
|
|
| |
c. |
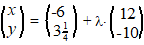 |
| |
|
|
|
|
| |
d. |
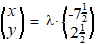 |
| |
|
|
|
|
| 3. |
Een rechte lijn gaat door (-2, 5) en
(4, 8)
Geef een vectorvoorstelling, een "gewone" vergelijking, en een
normaalvergelijking van die lijn. |
| |
|
|
|
|
| 4. |
De middelloodlijn van
twee punten P en Q is de lijn die door het midden van lijnstuk
PQ gaat, en die loodrecht op PQ staat. Het is de verzameling van
punten die gelijke afstand tot P als tot Q hebben.
Geef een vectorvoorstelling en een vergelijking van de
middelloodlijn van de punten (-2, 8) en (6, 12) |
| |
|
|
|
|
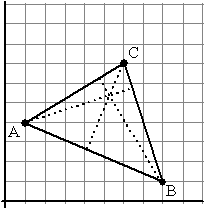
| 5. |
Gegeven is driehoek ABC
met de hoekpunten A(1, 4) en B(8, 1)
en C(6, 7).
Een hoogtelijn in een driehoek is een lijn vanaf
een hoekpunt loodrecht op de tegenoverliggende zijde.
Hiernaast zijn de drie hoogtelijnen van de driehoek getekend.
Stel vectorvoorstellingen van die hoogtelijnen op en laat zien
dat ze door één punt gaan. |
 |
| |
|
|
|
|
| |
|
|
|
|
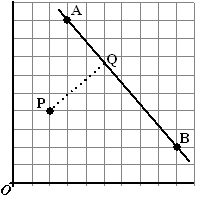
| 6. |
Hiernaast zie je lijn
AB door A(3, 9) en B(9, 2) en een punt P(2, 4)
Je moet van P naar lijn AB gaan via de kortst mogelijk route.
Dat is langs lijn PQ die loodrecht op AB staat. |
 |
| |
|
|
| |
a. |
Geef een vectorvoorstelling van AB |
| |
|
|
| |
b. |
Geef een vectorvoorstelling van PQ. |
| |
|
|
| |
c. |
Bereken de coördinaten van punt Q. |
| |
|
|
| |
d. |
Bereken de afstand PQ in twee decimalen
nauwkeurig. |
| |
|
|
|
|
| |
|
|
|
|
| 7. |
Op een cirkel met middelpunt (2,3)
en straal 13 ligt het punt R(7, -9)
Geef een vergelijking van de raaklijn aan de cirkel in punt R. |
| |
|
|
|
|
| 8. |
Examenopgave VEWO Wiskunde B, 2023-II
Gegeven zijn de
punten A(-2, -2), B(2, 2) en C(13/5
,84/5
) .
Lijn l is de lijn met de vectorvoorstelling: |
| |
|
|
|
|
| |
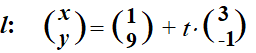 |
| |
|
|
|
|
| |
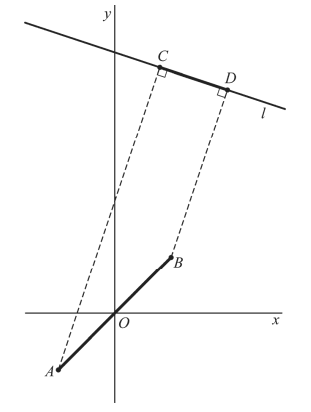
Het punt C
is de loodrechte projectie van A op lijn l en het punt
D is de loodrechte projectie van B op lijn l.
Zie de figuur. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Lijnstuk AB
is √k keer zo lang als lijnstuk CD. Hierin is k
een geheel getal.
Bereken exact
de waarde van k. |
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|