| 1. |
Sinds 1997 is er in Nederland geen militaire
dienstplicht meer. Daarvoor waren alle 18-jarigen
dienstplichtig. Dat betekende dat zij na een keuring een tijd in
het leger moesten doorbrengen. Bij die keuring werd je afgekeurd
(en hoefde je dus niet in dienst) als je te lang was.
Stel dat de gemiddelde lengte van de 18-jarigen in een jaar
normaal verdeeld was met een gemiddelde van 180 cm en een
standaarddeviatie van 16 cm.
Bij welke lengtes werd je in dat jaar dan afgekeurd als in
totaal 4% van de gekeurde mannen werd afgekeurd? |
| |
|
|
|
|
|
| 2. |
Het aantal cm neerslag in augustus in Nederland
is normaal verdeeld met een gemiddelde van 52,5 mm en een
standaardafwijking van 15,1 mm. |
| |
|
|
|
|
|
| |
a. |
Hoe groot is dan de kans
op meer dan 70 mm neerslag in zo'n maand? |
| |
|
|
| |
b. |
Hoe groot is de kans dat de
hoeveelheid neerslag méér dan 10 mm van het gemiddelde afwijkt? |
| |
|
|
|
|
|
| |
c. |
In mei is de gemiddelde neerslag
gelijk aan 66,3 mm, en de kans op minder dan 50 mm blijkt gelijk
te zijn aan 4%. Hoe groot is de standaarddeviatie van de
neerslag in mei? |
| |
|
|
|
|
|
| 3. |
Als er op een verpakking staat dat
de inhoud ervan bijvoorbeeld 300 gram is, dan moet dat ook
ongeveer kloppen.
Maar ja, als de vulmachines in fabrieken staan afgesteld op een
bepaald gewicht, dan is dat het gemiddelde gewicht van de
verpakkingen die ze vullen. Het vulgewicht is normaal verdeeld,
en vertoont dus een bepaalde spreiding.
Als een klant iets koopt waar op staat "Inhoud 300 gram" dan mag
slechts 3% van de verpakkingen minder dan 300 gram bevatten. |
| |
|
|
|
|
|
| |
a. |
Als een fabrikant zijn vulmachine
afstelt op 300 gram, hoeveel procent van de verpakkingen heeft
dan een gewicht minder dan 300 gram? |
| |
|
|
| |
b. |
De standaarddeviatie van het
vulgewicht van een bepaalde machine is 9 gram. Op hoeveel gram
moet de fabrikant zijn vulmachine dan afstellen zodat slechts 3%
een gewicht minder dan 300 gram heeft? |
| |
|
|
|
|
|
| |
|
| 4. |
(Examenvraagstuk).
Verkeersdrempels
zijn bedoeld om de snelheid van de automobilisten te beïnvloeden.
Afhankelijk van de gewenste snelheid in een straat worden de drempels
steiler of minder steil gemaakt. Zie de volgende afbeelding. |
| |
|
|
|
|
|
| |
 |
| |
|
|
|
|
|
| |
De
drempels met V85 = 50 zijn zo ontworpen dat 85% van de automobilisten de
drempel passeert met een snelheid van minder dan 50 km/uur.
In praktijk blijkt dat de passeersnelheid bij een drempel normaal
verdeeld is. Bij de drempels met V85 = 50 werd een gemiddelde
passeersnelheid van 43,1 km/uur gevonden met een standaardafwijking van
6,6 km/uur. |
| |
|
|
|
|
|
| |
a. |
Laat zien dat bij
deze verdeling inderdaad 85% van de automobilisten niet harder dan
50 km/uur rijdt. |
| |
|
|
|
|
|
| |
In
een kinderrijke wijk worden verkeersdrempels met V85 = 20 aangebracht.
Dat betekent dus dat 85% van de automobilisten de drempel passeert met
een snelheid van minder dan 20 km/uur. De passeersnelheid is ook nu
normaal verdeeld, maar met een kleinere spreiding: de standaardafwijking
is 2,1 km/uur. |
| |
|
|
|
|
|
| |
b. |
Bereken de
gemiddelde passeersnelheid in km/uur in 1 decimaal nauwkeurig bij dit
type drempels. |
| |
|
|
|
|
|
| |
|
|
|
|
|
| 5. |
Op het consultatiebureau houdt men
nauwkeurig de lengte van baby’s bij.
Het blijkt dat voor die lengte geldt: L = 20 + 10 •
√(t + 9).
Met L in cm en t in maanden met t = 0 het tijdstip
van de geboorte.
Natuurlijk zijn niet alle baby’s even lang: L is de gemiddelde
lengte.
De lengtes zijn normaal verdeeld en de standaarddeviatie blijkt
voor elke leeftijd 8 cm te zijn. |
| |
|
|
|
|
|
| |
a. |
Hoeveel procent van de baby’s van 7
maanden oud zal langer dan 70 cm zijn? |
| |
|
|
| |
b. |
Op welke leeftijd is 80% van de
kinderen langer dan 80 cm? |
| |
|
|
|
| |
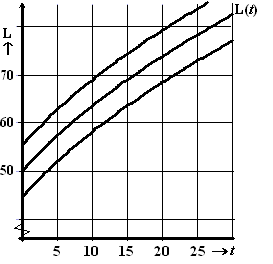
c. |
Om aan te geven wat nog
een redelijk normale lengte is heeft de arts van het
consultatiebureau in de figuur hiernaast de grafiek van L
getekend plus de twee lijnen waartussen 50% van de baby’s zich
bevindt.
Geef een vergelijking van de bovenste grafiek. |
 |
| |
|
|
|
|
|
| 6. |
Op de
kermis kon je vroeger vaak het gewicht van de Dikke Dame proberen te
raden. De deelnemers die er minder dan 5 kg vanaf zaten kregen een
prijs. |
| |
|
|
|
|
|
| |
a. |
Op een kermis
weegt de Dikke Dame 185 kg.
Op een avond wagen 1200 mensen een gokje. Het gewicht dat zij raden is
normaal verdeeld met een gemiddelde van 160 kg en een standaarddeviatie
van
12 kg. Hoeveel mensen
zullen een prijs krijgen? |
| |
|
|
|
|
|
| |
b. |
Op een andere
kermis is het gewicht dat de deelnemers raden ook normaal verdeeld met
een gemiddelde van 158 kg
en een standaarddeviatie van 15 kg. Het blijkt dat 6% van de deelnemers
een prijs krijgt.
Hoe zwaar was de Dikke Dame op deze kermis? |
| |
|
|
|
|
|
| 7. |
Als je iets meet wat groot is, dan
zal de fout in die meting gemiddeld ook groter zijn, dan als je
iets meet wat klein is. Dat klinkt logisch, vind je niet?
Mijn keukenweegschaal meet gewichten met een standaarddeviatie
die gelijk is aan 2% van het gemeten gewicht.
Ik ga een experiment verrichten en weeg met deze weegschaal 100
keer dezelfde biefstuk. (het is een beetje een saai experiment).
Van die 100 keer geeft de weegschaal 12 keer een gewicht lager
dan 350 gram aan.
Hoeveel weegt mijn biefstuk waarschijnlijk? |
| |
|
|
|
|
|
| 8. |
Een scholengemeenschap heeft de
eerste en tweede klassen nog gemengd HAVO-VWO, maar in de derde
klas wordt dat gescheiden. Om te kijken of de leerlingen
inderdaad in de derde klas op het juiste schooltype zitten houdt
men in de derde klas vrij snel een toets.
De scores op die toets blijken normaal verdeeld.
3VWO haalt een gemiddelde van 7,0 en 3HAVO haalt een
gemiddelde van 6,0. In beide gevallen is de standaarddeviatie
1,5.
In 3VWO zitten dit jaar 100 leerlingen, in 3HAVO 80 leerlingen. |
| |
|
|
|
|
|
| |
a. |
Hoeveel leerlingen zouden er moeten
overstappen als men vindt dat een score lager dan 5,5 bij HAVO
moet en een score hoger dan 7,0 bij VWO? |
| |
|
|
|
|
|
| |
b. |
Welke grensscore voor toelating tot
het VWO zou men moeten hanteren als men wil dat de 20% hoogst
scorende HAVO leerlingen alsnog naar het VWO gaan? |
| |
|
|
|
|
|
| 9. |
examenvraagstuk HAVO Wiskunde A,
1991. |
| |
|
|
|
|
|
| |
Na een grote en een kleine beurscrisis is de belegger
'risicobewuster' geworden. Aandelen leveren weliswaar een hoger
rendement dan een spaarrekening, maar ze zijn ook een stuk riskanter.
Onder rendement wordt hier verstaan de procentuele toename van het
belegde kapitaal per jaar.
In een prospectus van een beleggingsmaatschappij worden twee mogelijke
beleggingsfondsen aangeboden, waarbij gegevens over het risico worden
verstrekt . Zie de volgende tabel. |
| |
|
|
|
|
|
| |
| Fonds |
Gemiddeld
rendement |
Rendement met
95% kans tussen |
A
B |
5,7%
7,0% |
2,9% en 9,5%
-0,7% en 14,7% |
|
| |
|
|
|
|
|
| |
Bij de opgave van de mogelijke afwijking met een kans
van 95% gaat de maatschappij uit van de normale verdeling.
Ga bij de beantwoording van de volgende vragen uit van deze verdeling. |
| |
|
|
|
|
|
| |
a. |
Bereken de standaardafwijking van het
rendement bij fonds A |
| |
|
|
|
|
|
| |
b. |
Bereken bij fonds B de kans op een negatief
rendement. |
| |
|
|
|
|
|
| 10 |
examenvraagstuk VWO wiskunde A,
2016-II |
| |
|
|
|
|
|
| |
Een bedrijf produceert plastic verpakkingsmateriaal.
Men maakt er onder andere buisfolie. Buisfolie wordt verwerkt tot
plastic zakken. Bij de productie van de buisfoliezakken moet de
breedte binnen nauwe grenzen blijven. De streefwaarde is 715 mm.
Om het risico te beperken dat de zakken te smal zijn, wordt de
gemiddelde breedte ingesteld op 715,6 mm. Neem aan dat de breedte
normaal verdeeld is met σ = 0,5 mm.
Bij de productie van buisfoliezakken voor een
bepaalde afnemer is vastgelegd dat het tolerantiegebied het
gebied is waar de breedte van de zakken maximaal 1 mm van de
streefwaarde van 715 mm afwijkt. |
| |
|
|
|
|
|
| |
a. |
Bereken het percentage van de partij zakken dat
buiten dit tolerantiegebied ligt. |
| |
|
|
|
|
|
| |
Men vindt het productieproces voor een andere
afnemer van buisfoliezakken acceptabel als hoogstens 2,5% van de
zakken breder is dan 716 mm. Hiervoor moet de standaardafwijking wel
veranderen. Het is mogelijk de machine zo in te stellen dat de
gemiddelde breedte niet verandert maar de standaardafwijking wel. |
| |
|
|
|
|
|
| |
b. |
Beredeneer zonder berekeningen te maken of de standaardafwijking dan kleiner of
groter dan 0,5 moet zijn. |
| |
|
|
|
|
|
| |
c. |
Bereken hoe groot de
standaarddeviatie moet zijn. |
| |
|
|
|
|
|
| |
|
|
|
|
 |
 |
| |
|
|
|
|
|
| ©
h.hofstede (h.hofstede@hogeland.nl) |