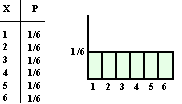|
|
 |
|
De Centrale Limietstelling. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
Vandaag heb ik zin om dingen bij
elkaar op te gaan tellen.
Zomaar....
Ik ga een aantal willekeurige dingen bij
elkaar optellen, en kijken wat dat oplevert.
Laten we beginnen met het gooien met een dobbelsteen en het aantal ogen
te tellen.
De kans op elk aantal is uiteraard 1/6 dus de
kansverdeling ziet eruit als hieronder:
Tot zover nogal een saai begin.
|
| Als tweede experiment gooien ik een muntstuk op en tel het aantal
keer kop. Dat is uiteraard 0 of 1, met beiden kans 1/2.
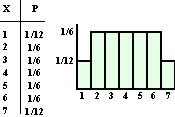
Het wordt al ietsje leuker als we die twee dingen (aantal kop en aantal
ogen) bij elkaar optellen. Dat geeft de kansverdeling hiernaast. |
 |
| Nog maar een experiment erbij
dan. Ik zet de TV aan en kijk naar de eerste twee gezichten die ik in
beeld krijg. Ik tel het aantal mannen daarbij en tel dat op bij de ogen
van de dobbelsteen en het aantal kop van de munt. Er vanuit gaande dat
de kans op man of vrouw 50% is, krijg ik de kansverdeling hiernaast.
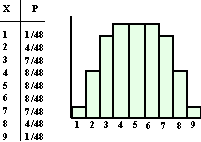
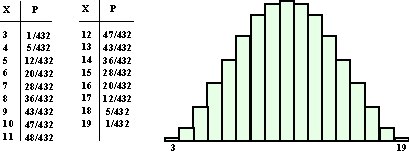
Dan schud ik een kaartspel en draai één voor één de kaarten om net
zolang tot ik een kaart krijg die geen plaatje is (dus een 2 tm 10). De
kans op elke is dus 1/9.
Ook de waarde van die kaart tel ik bij mijn som op.
Dat geeft de volgende kansverdeling: |
 |
|
|
 |
|
|
| |
Ik zou zo nog een tijdje door
kunnen gaan met willekeurige dingen bij mijn som op te tellen. De histogrammen die ik krijg vormen altijd zo'n soort filmpje
als hiernaast:
Dit soort filmpjes eindigt vreemd genoeg op den duur altijd met eenzelfde
soort klokvormachtige figuur.
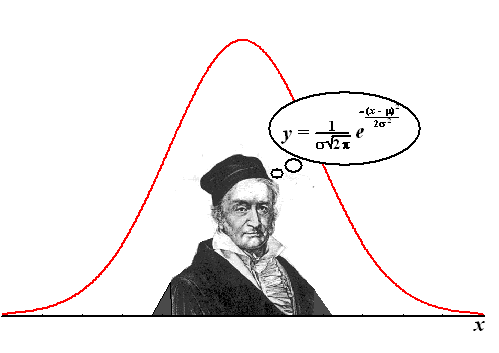
Het was de wiskundige Carl Friedrich Gauss die inzag dat die eindfiguren
niet zomaar ongeveer gelijk waren; nee hij ontdekte dat die figuren
PRECIES gelijk waren!!! Hij ontwikkelde zelfs een formule voor
deze figuur: |
 |
| |
|
 |
|
(een vrij technische afleiding uit de binomiale
verdeling staat hier) |
| |
|
Gauss ontdekte deze formule op
17-jarige (!!!) leeftijd. Deze ontdekking is zo belangrijk voor de
statistiek geworden, dat Gauss er in Duitsland zelfs het 10-mark biljet
mee haalde. Samen met zijn normale verdeling!
Wiskundigen noemen deze figuur en
deze kansverdeling de Normale Verdeling.
Natuurkundigen hebben het vaak over de Gauss-kromme.
Die ontdekking van Gauss heet de
Centrale Limiet Stelling: |
 |
| |
| Als je een heleboel
willekeurige dingen, die onafhankelijk van elkaar zijn en
allemaal hun eigen gemiddelde en standaarddeviatie hebben,
bij elkaar optelt, dan wordt het resultaat een normale
verdeling. |
|
|
|
"Ja, hoor eens", hoor ik je al denken, "Die
formule is natuurlijk wel mooi gevonden, maar dat dat zo'n soort
symmetrische vorm wordt, met een top in het midden en aflopend naar de
zijkanten, dat lijkt me nogal logisch! Met twee dobbelstenen gooi je
bijvoorbeeld vaker 7 dan 12 omdat 7 gewoon op veel meer manieren kan
voorkomen. Zo apart is die vorm eigenlijk helemaal niet..."
Toch is dat niet waar. Die vorm is wél apart....
Laten we een valse dobbelsteen nemen waarvan de kansverdeling helemaal
niet symmetrisch is, maar helemaal scheef naar één kant:
Misschien verwacht je nu dat, omdat de kansverdeling van het aantal
ogen van deze ene steen scheef naar rechts oploopt (kansen
1/6 - 2/6
- 3/6), dat de verdeling als je een groot
aantal van deze worpen bij elkaar optelt ook wel scheef naar rechts zal
zijn. Maar dat is niet zo!
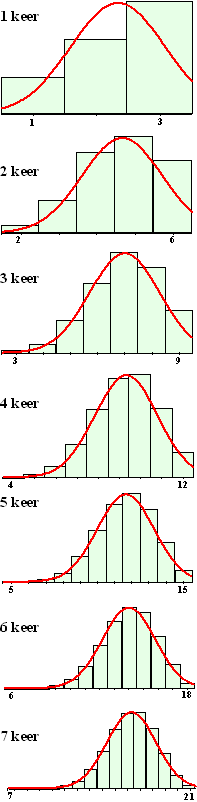
Kijk maar naar de serie afbeeldingen hiernaast. Bij één keer gooien is
het uiteraard wel scheef, maar bij vaker gooien wordt dat steeds minder
en verschijnt toch weer de rood getekende klokvorm! Tuurlijk, aan de
linkerkant zit een langere "staart" dan aan de rechterkant, maar de
kansen daar zijn te verwaarlozen (ongeveer nul). Het gedeelte "waar het
om gaat" heeft weer die mooie symmetrische klokvorm.
Kijk maar in de figuur hieronder hoe voor deze scheve oorspronkelijke
kansverdeling de somverdeling langzaam naar rechts wandelt en tijdens
dat wandelen een steeds mooiere klokvorm gaat aannemen:
|
 |
|
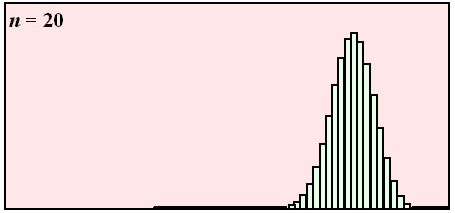
De laatste verdeling moet je nog maar even rustig
bekijken. Hieronder zie je hoe de som van 20 zulke worpen met zo'n
supervalse dobbelsteen eruit ziet: |
|
|
|
 |
| |
|
| Inderdaad toch weer een aardig
mooie klokvorm, maar wel met aan de linkerkant een veel grotere staart
(die er niet toe doet) dan aan de rechterkant. |
| |
|
|
Waarom is de normale verdeling
eigenlijk zo belangrijk? |
| |
|
| Omdat de normale verdeling elke
keer ontstaat als een groot aantal willekeurige factoren wordt opgeteld
komt hij erg vaak voor. Immers, bijna alles wat wij meten is gevolg van
een groot aantal factoren; gewicht, lengte, IQ, temperatuur, behaalde
proefwerkcijfers, meetfouten, noem maar op. |
|
|
|
Eigenschappen van de normale
verdeling. |
| |
|
| De normale verdeling heeft een
aantal handige en belangrijke eigenschappen: |
| |
|
|
• |
Hij wordt volledig bepaald door twee getallen: het
gemiddelde μ en de standaarddeviatie σ (ook wel
standaardafwijking genoemd).
Dat kun je zien aan die moeilijke formule van Gauss.
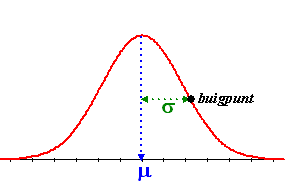
Het gemiddelde
μ vind je "natuurlijk"
in het midden. De standaarddeviatie
σ
bepaalt hoe breed de klokvorm wordt. Om precies te zijn is het
de horizontale afstand vanaf het midden naar de buigpunten van
de figuur. Dat zijn de punten waar de grafiek van "hol" overgaat
naar "bol". |
| |
 |
| |
|
| |
Dus als je m verandert dan
schuift de klokvorm in zijn geheel naar links of naar rechts en
als je
σ verandert, dan wordt de
klokvorm breder of smaller maar blijft het midden op zijn
plaats. |
| |
|
|
• |
De totale oppervlakte onder de normale verdeling is 1.
Bedenk dat daar eigenlijk heel veel kleine staafjes van een
histogram onder de klokvorm staan. De totale oppervlakte van een
histogram is gelijk aan de totale frequentie, en als je op de
y-as procenten zet komt daar 100% uit. "Alles samen is
100%". |
| |
|
|
• |
De klokvorm is symmetrisch.
Je kunt hem spiegelen in de lijn x =
μ. Dat is natuurlijk nogal logisch als je je bedenkt dat
hij gevolg is van heel veel willekeurige factoren. Als die echt
willekeurig zijn zullen ze even vaak een bijdrage kleiner dan
μ leveren als een bijdrage groter dan
μ.
Van deze verdeling zijn het gemiddelde en de mediaan en de modus
alledrie aan elkaar gelijk. |
| |
|
|
• |
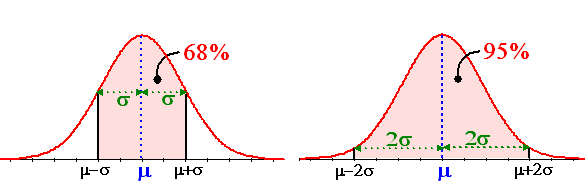
Twee vuistregels.
Tussen de grenzen x =
μ -
σ en x =
μ
+
σ blijkt ongeveer 68% van de
oppervlakte te zitten.
Tussen de grenzen x = μ -
2σ en x =
μ + 2σ blijkt ongeveer
95% van de oppervlakte te zitten. |
| |
|
| |
 |
| |
|
|
| |
|
|
OPGAVEN |
| |
|
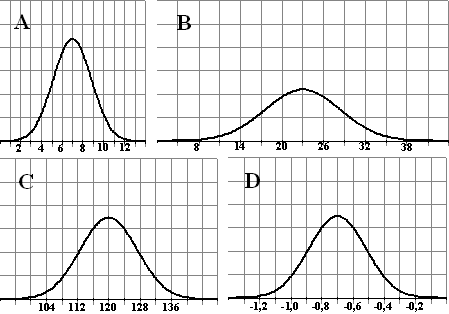
| 1. |
Hieronder staan vier klokvormen getekend. |
| |
|
|
|
|
|
 |
| |
|
|
|
|
| |
a. |
Bepaal zo goed mogelijk van elk van
die klokvormen
m en s. |
| |
|
|
| |
b. |
Maak een schatting voor de
schaalverdeling van de y-as. |
| |
|
|
|
|
| 2. |
Klokvormen die hoger zijn, zijn ook altijd
smaller. Leg uit waarom dat logisch is. |
| |
|
|
|
|
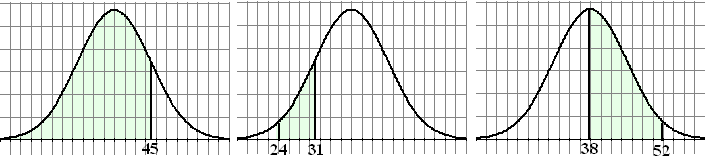
| 3. |
De normale verdelingen die hieronder
zijn getekend horen allemaal bij
μ =
38 en
σ = 7
Geef van elk van de gekleurde gebieden de oppervlakte. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| 4. |
Teken bij elk van de volgende
gevallen een klokvorm en gebruik die om de vraag te
beantwoorden. |
| |
|
|
|
|
| |
a. |
Het gewicht van zakken potgrond is
normaal verdeeld met een gemiddelde van 20 kg en een
standaarddeviatie van 0,8 kg. Hoeveel procent van de zakken zal
een gewicht tussen de 18,4 en 20,8 kg hebben? |
|
| |
|
|
|
| |
b. |
De lengte van de brugklassers dit
jaar is normaal verdeeld met een gemiddelde van 165 cm en een
standaarddeviatie van 16 cm. Het blijkt dat 39% van hen korter
is dan 160 cm. Hoeveel procent zal dan tussen de 170 en 181 cm
lang zijn? |
|
| |
|
|
|
| |
c. |
Een bioloog meet de vliegsnelheid
van een groot aantal zwaluwen en vindt een gemiddelde van 60
km/uur met een standaarddeviatie van 8 km/uur. Het blijkt dat
bij 21% van de metingen de snelheid tussen 65 km/uur en 76
km/uur lag. Bij hoeveel procent van de metingen zal de snelheid
dan kleiner dan 55 km/uur zijn geweest? |
|
| |
|
|
|
|
| 5. |
In welk van de volgende gevallen zal
er, denk je, (ongeveer) sprake zijn van een normale verdeling? Als
dat niet het geval is, leg dan uit waarom volgens jou niet. |
| |
|
|
|
|
| |
a. |
Het jaarinkomen van de Nederlanders. |
| |
b. |
De herseninhoud van volwassen mannen
in Groningen. |
| |
c. |
De levensduur van 1,5 Volt AA
batterijen van Duracel. |
| |
d. |
De tijd die je moet wachten op een
tramhalte als die tram precies één keer per half uur komt, en je
weet niet wanneer. |
| |
e. |
De gemiddelde afstand tussen huis en
school van middelbare scholieren. |
| |
f. |
De zwangerschapsduur van Belgische
vrouwen. |
| |
g. |
Het aantal dagen dat het duurt
voordat klanten hun rekening betalen. |
| |
|
|
| 6. |
Het IQ van alle Nederlanders is
normaal verdeeld met een gemiddelde van 100.
Leg uit waarom het IQ van de VWO-leerlingen in Nederland dan
NIET normaal verdeeld zal zijn. |
| |
|
|
|
|
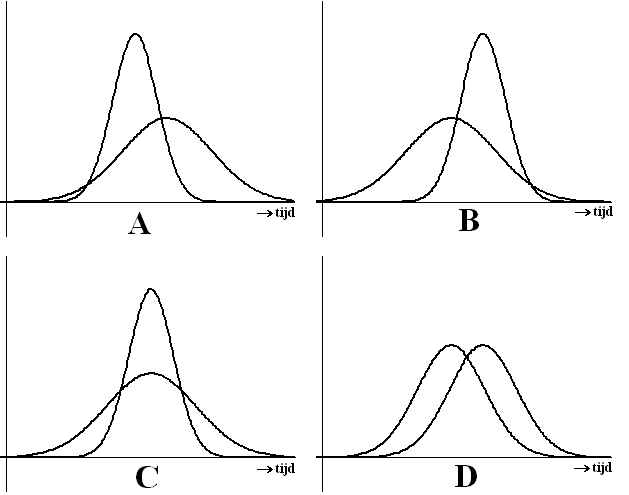
| 7. |
Examenvraagstuk HAVO wiskunde A,
2007. Men heeft een onderzoek
gedaan onder studenten. Daarbij is gekeken naar de
tijd die mannelijke en vrouwelijke studenten thuis aan hun studie
besteden. Het onderzoek wijst uit dat vrouwen per week meer tijd aan
‘huiswerk’ besteden dan mannen. De spreiding in
huiswerktijd bij de mannen is kleiner dan bij de
vrouwen. Bij beide is hier bij benadering ook weer sprake van een
normale verdeling.
Vier leerlingen kregen de opdracht om in één figuur van zowel de
mannelijke als de vrouwelijke studenten een
verdeling van de tijd aan te geven die de studenten
thuis aan hun studie besteden. Het resultaat van deze opdracht staat
in onderstaande figuur. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Eén van de bovenstaande figuren past
het best bij de gegevens over de studenten.
Welke figuur is dat? Licht je antwoord toe. |
| |
|
|
|
|
| |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|