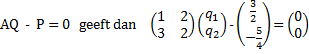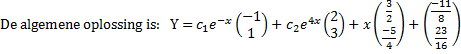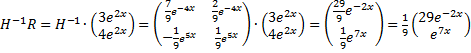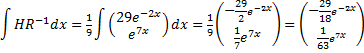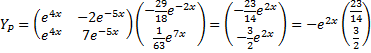niet-homogene vergelijkingen


	© h.hofstede (h.hofstede@hogeland.nl)

Stelsels Niet-Homogene Differentiaalvergelijkingen

De niet-homogene vergelijking is in het algemeen te schrijven als:

Y' = A • Y + R

Daarbij is Y' = A • Y de homogene vergelijking en is A een 2 ´ 2 matrix en zijn Y' en Y en R vectoren.
We weten intussen uit de vorige lessen hoe we oplossingen van de homogene vergelijking kunnen vinden, en ook dat de algemenen oplossing een combinatie is van de oplossingen van de homogene vergelijking plus een particuliere oplossing.
Het gaat er in deze les om. om die particuliere oplossing te vinden.

Voor "gewone" tweede orde differentiaalvergelijkingen hadden we twee manieren om een particuliere oplossing van een niet-homogene vergelijking te vinden. Dat waren de volgende twee:

1. Onbepaalde coëfficiënten. Dat stond in deze les.

Je gokte gewoon een particuliere oplossing (daarbij goed kijken naar het niet-homogene deel R).
Bij e^ax was dat meestal P • e^ax en bij sinax was het meestal P • sinax + Q • cosax
Door in te vullen in de hele differentiaalvergelijking kun je dan die onbepaalde coëfficiënten P en Q vinden.

2. Variatie van parameters. Dat stond in deze les.

Probeer y = c₁y₁ + c₂y₂
Als je dan eist dat c₁' • y₁ + c₂' • y₂ = 0 dan hou je over c₁' • y₁' + c₂' • y₂' + r = 0 en uit die twee vergelijkingen kun je c₁' en c₂' oplossen, die je daarna hopelijk kunt primitiveren om c₁ en c₂ te vinden.

Nou, bij stelsels vergelijkingen gaat het eigenlijk precies zo!!!
Het enige verschil is, dat die coëfficiënten c, P en Q nu allemaal vectoren zijn in plaats van gewone functies.

Onbepaalde coëfficiënten.

Kijk maar naar het volgende voorbeeld en waarschijnlijk wordt alles wel duidelijk (bedenk dat hoofdletters steeds vectoren/matrices zijn)

voorbeeld: Los dit stelsel op: y₁' = y₁ + 2y₂ + x en y₂' = 3y₁ + 2y₂ - 2x
Dat kun je natuurlijk ook zo noteren:

Laten we die matrix en die vector een naam geven: Y ' = A • Y + x • R
Voor het oplossen van de homogene vergelijking laten we dat laatste stuk x • R weg, en moeten we de eigenwaarden en eigenvectoren van matrix A zoeken. Dat doe je zelf maar; er komen eigenwaarden l = 4 en l = -1 uit, en de algemene oplossing van de homogene vergelijking is:

En nu de particuliere oplossing nog eventjes eraan toevoegen.....
Omdat dat homogene stuk lineair is (x en -2x) proberen we een particuliere oplossing van de vorm Y = xP + Q
Daarbij zijn P en Q ook weer vectoren natuurlijk.
Dat geeft Y ' = P en dat kun je invullen in de oorspronkelijke differentiaalvergelijking:
P = A • (xP + Q) + xR
Neem de stukken met x bij elkaar en de losse resten ook: x(AP + R) + (AQ - P) = 0
Omdat dat voor elke x moet gelden, moeten beide termen afzonderlijk nul zijn, dus AP + R = 0 en AQ - P = 0

Dat geeft p₁ + 2p₂ + 1 = 0 en 3p₁ + 2p₂ - 2 = 0 met als oplossing p₁ = ³/₂ en p₂ = -⁵/₄ (makkie!)

Dat geeft q₁ + 2q₂ - ³/₂ = 0 en 3q₁ + 2q₂ + ⁵/₄ = 0 met als oplossing q₁ = -¹¹/₈ en q₂ = ²³/₁₆

Variatie van Parameters.

De oplossingen van de homogene vergelijking zijn nu    e^λ1^{x
•} C₁ en e^λ2^x • C₂ waarbij die λ's de eigenwaarden van A zijn, en die C's de bijbehorende eigenvectoren. Laten we deze homogene oplossingen samen in één 2 × 2 matrix H zetten, zodat elke kolom van H een oplossing is van de homogene vergelijking.

Probeer nu als particulier oplossing Y_P = H • X met C nog één of andere onbekende vector.
Dan is de afgeleide (met de productregel):   Y_P' = H ' • X + H • X'
Vul nu de formules voor Y_P en Y_P' in de oorspronkelijke differentiaalvergelijking in:
Dat geeft   H' • X + H • X' = A • H • X + R    ....(1)

Maar omdat H een oplossing van de homogene vergelijking is, geldt dat   H' = A • H dus HX = A• HX
Dan vallen in vergelijking (1) die twee stukken HX en AHX tegen elkaar weg en blijft er over:   H • X'= R

Y_P = H • X geeft H • X' = R

Die laatste geeft ons de mogelijkheid om X' te berekenen, namelijk door beide kanten met H^-1 te vermenigvuldigen.
Dat geeft X' = H^-1 • R en vervolgens is X te vinden als we die X' kunnen primitiveren.

X = ∫ H^-1• Rdx (en dan is Y_P = H • X)

Hopelijk lukt dat allemaal.
(die inverse H' vinden lukt trouwens zeker wel, want we weten al dat H was opgebouwd uit onafhankelijke oplossingen dus heeft H determinant ongelijk aan nul).

Uitgeschreven voorbeeld Los op y₁' = 2y₁ + 2y₂ + 3e^x en y₂' = 7y₁ - 3y₂ + 4e^2x

De algemene oplossing van de homogene vergelijking is: (los dat zelf maar op, dat kun je wel intussen)

We gaan nu Yp = H • X proberen.
Je kunt nu direct die X vinden door X = ∫ H^-1• Rdx van hierboven te gebruiken. Voor de grap gaan we het één keer toch nog uitschrijven zodat je ietsje beter ziet wat er nou precies gebeurt.
Komt ie:

Vul nu Y_P = H • X in de oorspronkelijke differentiaalvergelijking in (met de productregel voor Y_P' ):

Omdat H een oplossing van de homogene vergelijking is, zijn de eerste term aan de linkerkant en die eerste term aan de rechterkant aan elkaar gelijk en vallen ze weg (immers Y' = AY), zodat overblijft:

Vermenigvuldig nu beide kanten met de inverse van die eerste matrix. (Die H^-1 geef ik zonder uitleg: schoonvegen, weet je nog? Staat hier. )

En nu nog even H^-1R primitiveren:

Dat geeft dan eindelijk de particuliere oplossing Y_P = H • X:

De algemene oplossing is dan: