 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
Lengte of Oppervlakte of Inhoud? |
| |
|
|
Erg vaak wordt geprobeerd door
leuke plaatjes de grafieken uit een verslag wat "op te fleuren".
"Het oog wil ook wat, nietwaar?"
Toch moet je daarmee uitkijken.....
|
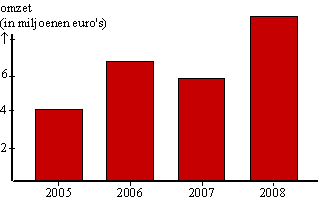
Hiernaast zie je een staafdiagram
van de omzet van het bedrijf Friesche Vlag in een deel van
Nederland.
Het lijkt redelijk goed te gaan want er is een soort van stijging te
zien over de laatste jaren.
Om het financiële verslag wat op te leuken voor de aandeelhouders
besluit de financieel directeur de nogal saaie staven te vervangen door
melkpakken, met precies de goede hoogte die bij de behaalde omzet hoort.
Dat levert de volgende figuur:
|
 |
|
 |
| |
|
|
Dat ziet er inderdaad
veel leuker uit, maar alhoewel alle hoogtes precies goed zijn getekend
klopt het nu toch niet meer!
Dat zit zo:
Tussen 2005 en 2008 is de omzet gestegen van 4,0 naar 9,3 miljoen, en
dat is een factor 9,3/4,0 ≈ 2,3. Daarom
is het pak van 2008 precies 2,3 keer zo hoog gemaakt als het pak van
2005. Het plaatje is gewoon 2,3 keer vergroot.
Maar onder de "hoeveelheid" bij een melkpak versta je natuurlijk de
inhoud ervan. En als je alle afmetingen van een figuur 2,3 keer
vergroot, dan wordt de inhoud maar liefst 2,33
≈ 12 keer zo groot! In dat laatste pak melk
gaat 12 keer zoveel melk als in het eerste !!
Voor ons gevoel is de groei bij deze afbeeldingen met melkpakken dus
veel groter dan in werkelijkheid. Maar goed, misschien is dat wel
precies wat de financieel directeur graag wilde bereiken....... |
| |
|
|
| |
|
|
 |
|
|
 |
|
schaalverdelingen |
|
|
absoluut, relatief |
|
| |
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Hieronder zie je een aantal bankbiljetten,
allemaal even groot getekend: |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Teken deze bankbiljetten zodanig ten
opzichte van elkaar dat de lengtes ervan in
verhouding staan tot de waarde. |
| |
|
|
|
| |
b. |
Teken deze bankbiljetten zodanig ten
opzichte van elkaar dat de oppervlakten ervan
in verhouding staan tot de waarde. |
| |
|
|
|
| 2. |
De staatsloterij gebruikt voor de
reclame afbeeldingen van vissen die de jackpot voorstellen. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
De grote vis stelt de hoofdprijs van
27,5 miljoen voor, en de kleine de prijs van 5,5 miljoen. Zo te
zien zijn de vissen een vergroting/verkleining van elkaar.
Onderzoek of de verhoudingen tussen de inhoud (dat is immers het
gewicht van de vis die je aan de haak slaat) van de vissen
inderdaad klopt met het geldbedrag dat zij voorstellen.
Als dat niet zo is, teken dan de kleine vis op een formaat dat
wél klopt. |
| |
|
|
|
| 3. |
De Nederlandse regering wil de
komende jaren bezuinigen op de kunstsubsidies.
In 2010 was het totale budget nog 430 miljoen euro, maar aan de
plaatjes hieronder zie je wel dat dat de komende jaren fors gaat
afnemen. |
| |
|
|
|
| |
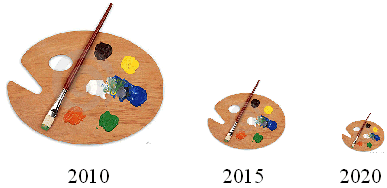 |
| |
|
|
|
| |
a. |
Hoe groot zal het subsidiebedrag in
2020 zijn als de breedte van de paletten in verhouding tot het
subsidiebedrag staan? |
| |
|
|
|
| |
b. |
Hoe groot zal het subsidiebedrag in
2020 zijn als de oppervlakte van de paletten in verhouding tot
het subsidiebedrag staan? |
| |
|
|
|
| |
c. |
Als het subsidiebedrag in 2015 nog
208 miljoen zal zijn gaat het dan om de afmetingen van de
paletten of om de oppervlakten? |
| |
|
|
|
| 4. |
In de tabel hiernaast
zie je de uitgaven aan defensie van Nederland, China en de VS
in 2008.
Stel dat je daar een leuk plaatje van wil maken met geldzakken
waarbij de geldzak die bij China hoort er zó uitziet:
|
| land |
uitgaven
in miljarden dollars |
Nederland
China
VS |
8,5
65
696 |
|
| |
Welk van de volgende plaatjes hoort
dan bij Nederland en welk bij de VS? Bedenk dat de hoeveelheid
geld afhangt van de inhoud van zo'n geldzak. |
| |
|
|
|
|
 |
| |
|
|
|
| |
|
|
|
| |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|