transformaties logaritmen


Formules veranderen.	© h.hofstede (h.hofstede@hogeland.nl)

Deze les gaat het erom dat je een formule die eruit ziet als y = ..(iets met x)...... verandert in een formule x = ...... (en dan staat daar iets met y)..... We zeggen in zo'n geval ook wel: "Druk x uit in y"

Druk x uit in y ⇔ maak een formule x = .....(y).....

De nieuwe formule heet dan de inverse (= omgekeerde) van de oude.

voorafje: ²/₇ = ¹/₇• 2

Ja dûh....hoor ik je al denken..... logisch!!!
Maar toch... zodra het gaat om letters in plaats van getallen wordt dit simpele regeltje gauw vergeten.
Dan zie je toch vaak in formules iets staan als ^{(5x
-
6)}/₂ terwijl dat natuurlijk hetzelfde is als ¹/₂ • (5x - 6) = 2¹/₂x - 3
Dat laatste staat beter en werkt ook makkelijker in formules.

Met breuken wordt het nog mooier. Neem bijvoorbeeld iets als y = ¹/₅x + 2.
Als je daar x = ... van wilt maken krijg je eerst y - 2 = ¹/₅x en daarna
x = ^{(y - 2)}/_0,2Maar dat kun je veel mooier schrijven:
x = ¹/_0,2 • (y - 2) = 5 • (y - 2) = 5y - 10

hoofdmaaltijd: logaritmen en exponenten.

Voor de honderdste keer nog maar weer eens de hoofdregel om logaritmen en machten in elkaar te veranderen:

g^x = a ⇔ x = ^glog a

Dat gaan we nu gebruiken om logaritme-formules en exponenten-formules in elkaar om te zetten

Voorbeeld 1: Gegeven y = 6 + 3 • 2^{x - 1}. Druk x uit in y.

Oplossing: met de balansmethode geeft dat achtereenvolgens:

y = 6 + 3 • 2^{x - 1}y - 6 = 3 • 2^{x - 1}
¹/₃y - 2 = 2^{x - 1}
²log(¹/₃y - 2) = x - 1
1 + ^0,5log(¹/₃y - 2) = x
x = 1 + ^0,5log(¹/₃y - 2)

Voorbeeld 2: Gegeven is y = 4 - 2 • ⁹log(x - 4). Druk x uit in y

Oplossing: alweer met de balansmethode:

y = 4 - 2 • ⁹log(x - 4)
y - 4 = -2•⁹log(x - 4)
-0,5y + 2 = ⁹log(x - 4)
9^{-0,5y + 2} = x - 4
x = 4 + 9^{-0,5y + 2}

toetje.

Als je klaar bent kun je soms de formule voor x nog wat "netter" gaan schrijven. Er kan ook in een opgave gevraagd worden om de formule voor x in een bepaalde vorm te geven. Daarvoor zul je de rekenregels voor machten en logaritmen die je hebt geleerd moeten gebruiken.
De twee voorbeelden hierboven zouden er ook zó kunnen uitzien:

Voorbeeld 1 (vervolg): Gegeven y = 6 + 3 • 2^{0,5x - 1}. Schrijf deze formule in de vorm x = ^alog(by + c)
Dan zou je na het eerste deel hierboven zó verder moeten gaan:

x = 1 + ^0,5log(¹/₃y - 2)
x = ^0,5log(¹/₂) + ^0,5log(¹/₃y - 2)x = ^0,5log(¹/₂ • (¹/₃y - 2))
x = ^0,5log(¹/₆y - 1)
Dus a = ¹/₂en b = ¹/₆en c = 1.

Voorbeeld 2 (vervolg): Gegeven is y = 4 - 2 • ⁹log(x - 4). Schrijf deze formule in de vorm x = a + b • g^y
Dan zou je na het eerste deel hierboven zó verder moeten gaan:

x = 4 + 9^{-0,5y + 2}
x = 4 + 9^-0,5y• 9²
x = 4 + (9^-0,5)^y • 81
x = 4 + 81 • (¹/₃)^y
Dus a = 4 en b = 81 en g = ¹/₃

't Kost even meer moeite, maar dan héb je ook wat...

OPGAVEN

Druk x uit in y:

y = 2 + log(x - 1)

y = 1 - 2 • 3^x+4

y = 4 • log(¹/₂x) - 1

Geert en Cobi zijn twee erg regelmatige en erg gezellige wijndrinkers. Eind 2005 weet Geert nog snel belastingvrij twee vaten wijn met elk 500 liter op de kop te tikken. Zo hebben ze elk hun eigen vat.
Hij de Médoc, zij de Bordeaux.
Geert begint het nieuwe jaar direct aan zijn vat. Hij houdt van regelmaat en drinkt elke dag 0,8 liter op.
Cobi heeft zich weer eens voorgenomen te stoppen met alcohol. Ze houdt het inderdaad een hele tijd vol, maar na precies 100 dagen in het nieuwe jaar wordt het haar teveel. Op dag 101 breekt ze ook haar vat aan. Om toch wat te minderen heeft ze een slim plannetje bedacht: ze drinkt elke dag 0,5% van de hoeveelheid die in het vat zit. Die hoeveelheid neemt langzaam af, dus ook de hoeveelheid die ze drinkt. Slim hé?
Noem de hoeveelheid in de vaten van Geert en Cobi respectievelijk G(t) en C(t)

De volgende formule blijkt te gelden: C(t) = 825,4 • 0,995^t waarbij t het eind van de dag voorstelt.

Leid deze formule zelf af.

Volgens de richtlijnen van de AA is iemand alcoholist als zij meer dan 0,8 liter per dag drinkt.

Bereken algebraïsch hoe lang Cobi volgens deze normen alcoholist zal zijn.

t = 328

Bepaal op welke dag de vaten van Geert en Cobi even vol zullen zijn.

t = 158

Cobi wil graag direct weten wanneer er nog een bepaalde hoeveelheid wijn in haar vat zit. Daartoe ontwikkelt zij de formule: t = 1340 - 460 • log(C)
Bereken de beide constanten in deze formule in twee decimalen.

1339,81 en 459,36

Vanaf het moment dat wij geboren worden sterven er bij ons hersencellen af. In het begin nog haast niet, maar het worden er meer en meer. Voor iemand in HAVO 5 zijn er al heel wat hersencellen afgestorven.
Een bioloog heeft de volgende formule opgesteld waarmee volgens hem de relatie tussen het aantal afgestorven hersencellen (H) en de leeftijd (L) redelijk goed wordt weergegeven:
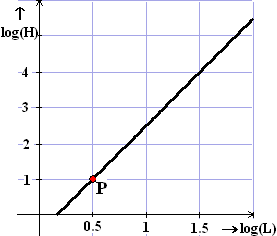
log(H) = -0,5 + 3 • log(L)

Hij maakt de grafiek hiernaast, waarbij hij log(H) op de y-as uitzet tegen log(L) op de x-as. Het punt P betekent bijvoorbeeld dat er bij een kind van ongeveer 3 jaar ongeveer 10 hersencellen zijn afgestorven

Leg duidelijk uit waarom dat zo is.

Bij mij zijn er ongeveer 22000 cellen afgestorven. Bereken algebraïsch mijn leeftijd.

41 jaar

De formule hierboven is ook te schrijven als H ≈ 0,32 • L³Bewijs dat, en bereken met deze formule wanneer iemand ongeveer 600 hersencellen per jaar verliest.

25 jaar

Examenvraagstuk (gewijzigd).

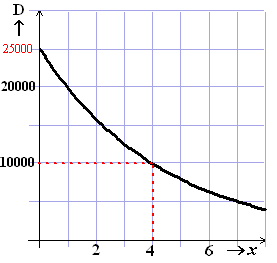
Wijken in een stad die dichter bij het centrum liggen zijn dichter bevolkt dan wijken verder van het centrum af. In 1950 begon men een onderzoek naar het verband tussen de bevolkingsdichtheid in een stad en de afstand tot het stadscentrum. De bevolkingsdichtheid D in een punt P is het aantal inwoners in een cirkelvormig gebied rond P met een oppervlakte van 1 km². In de figuur hiernaast zie je een grafiek die voor een bepaalde stad het verband tussen de afstand x tot het stadscentrum (in km) en de bevolkingsdichtheid D weergeeft. Uit deze grafiek kun je aflezen dat op een afstand van 4 km van het stadscentrum de bevolkingsdichtheid gelijk is aan 10000 inwoners per km² .

Bij de getekende grafiek hoort de formule D = a • 2^-bx .
Hierin zijn a en b constanten.

Bereken met behulp van de figuur de waarden van a en b. Rond in je antwoord gevonden waarden die niet geheel zijn af op twee decimalen.

a=25000, b≈0,33

Voor een andere stad heeft men het volgende lineaire verband tussen ³log(D) en x gevonden: ³logD = 9 - 0,2x

Toon algebraïsch aan dat bij benadering geldt: D = 19700 • 0,8^x

Hoeveel meter moet je vanuit het centrum van een stad weglopen om de bevolkingsdichtheid te laten halveren? Geef een exacte berekening met behulp van de formule in vraag b)

≈ 3,1

De antropoloog Ehrenberg stelde een verband vast tussen de lengte (h in m) en het gewicht (w in kg) van kinderen tussen 5 en 13 jaar. Hij vond: log w = 0,8h + 0,4
Deze relatie blijkt alom te gelden, onafhankelijk van de sociale klasse of het ras van een kind. De WHO (World Health Organisation) gebruikt deze relatie om ondervoeding bij kinderen vast te stellen.

Bereken algebraïsch het normale gewicht van een kind van 124 cm lang.

24,7 kg

Deze relatie is te schrijven als w = a • g^h
Toon dat aan, en bereken a en g.

a≈2,51 en g≈6,31

Ehrenberg zelf presenteerde zijn relatie als log w = 0,8h + 0,4 ± 0,04, waarmee hij aangaf binnen welke grenzen een kind als normaal gezien kon worden.

Een bepaald kind heeft een lengte van 154 cm en een gewicht van 35 kg. Dat is te licht. Het wordt daarom als ondervoed beschouwd.

Hoe zou het gewicht van het kind moeten veranderen om binnen de normale grenzen te komen?

39,1 - 47,0 kg

Het kan echter ook zijn dat de lengte verkeerd is gemeten! Hoe zou de lengte moeten veranderen om met dit gewicht binnen de normale grenzen te komen?

138-148 cm

Hoe zou je de ± 0,04 in de constanten in de formule van vraag b kunnen opnemen?

2,29 < a < 2,75

In de 18^e eeuw al vonden de astronomen Titius en Bode een verband tussen het nummer (n) van een planeet en de afstand tot de zon (R). Daarvoor moet de afstand R worden gemeten in A.E. (zgn. astronomische eenheden, met 1A.E. = afstand aarde-zon = 150 miljoen km).
Dat verband was: R(n) = 0,4 + 0,3 • 2ⁿ

Saturnus heeft afstand 1490 miljoen kilometer tot de zon. Welk nummer hoort bij Saturnus?

De volgende formule geeft je het nummer van een planeet als zijn afstand (in A.E.) bekend is:
n(R) = 1,7 + 3,3log(R - 0,4)
De getallen 1,7 en 3,3 daarin zijn afgeronde getallen.
Bereken deze getallen in drie cijfers achter de komma.

1,737 en 3,322

Voor de filmgevoeligheid van een filmrolletje zijn er twee verschillende schalen in omloop.
ASA (American Standard Association) en DIN (Deutsches Institut für Normung) berusten op de kleinste hoeveelheid licht die nog een afdruk op de fotografische film doet ontstaan.
Om de schalen in elkaar om te rekenen kun je de volgende formule gebruiken:
DIN = 15 + 3 • ²log(^ASA/₂₅)

Toon aan dat deze formule ook te schrijven is als DIN = p • logASA + q

Toon aan dat deze formule ook te schrijven is als ASA = a • 2^{b • DIN}

Leg met beide formules (van vraag a) en van vraag b)) uit hoeveel groter DIN wordt als ASA verdubbelt.

Boerenkool smaakt lekkerder als er "een nacht vorst overheen is geweest". Daarom stop ik gekochte boerenkool altijd direct in mijn vriezer. Voor de temperatuur van de boerenkool in de vriezer geldt: T(t) = 35 • 2^-0,5t - 16.
Daarin is t de tijd in uren met t = 0 het moment dat ik de boerenkool in de vrieskist stop.

Op welke temperatuur is de vrieskist ingesteld? En welke temperatuur heeft de boerenkool op t = 0?

-16ºC en 19ºC

Na hoeveel minuten is de temperatuur 4 ºC?

1,61 uur

De formule is te herleiden tot t = a • ²log(bT + c) . Bereken a, b en c.

-2, ¹/₃₅, ¹⁶/₃₅

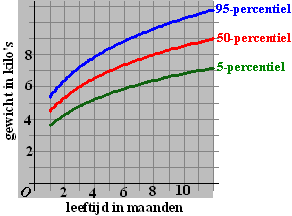
Hiernaast zie je drie groeicurves voor meisjes tussen 1 en 12 maanden oud. De rode grafiek is het gemiddelde, onder de groene grafiek ligt 5% van de meisjes, en boven de blauwe ligt ook 5%

Bij de rode grafiek hoort de vergelijking:
G = 6,52•log(t + 1,82) + 1,56

Deze vergelijking is ook te schrijven als: G = 6,52 • log(at + b)

Toon dat aan en bereken a en b.

1,7348 en 3,1574

Bij de blauwe grafiek hoort de vergelijking: G = 7,82 • log(t + 1,82) + 1,87

Deze vergelijking is ook te schrijven als t = a • b^G + c

Toon dat aan en bereken a en b en c.

0,576 en 1,342 en -1,82

10.

examenvraagstuk HAVO Wiskunde B, 1989.

Van een diersoort in een bepaald gebied wordt het aantal N afhankelijk van de tijd t bekeken. Er blijkt dat log N lineair afhangt van log t volgens de formule: logN = 3 + 0,75 • logt voor t ≥ 1
N kan geschreven worden in de vorm N = a • t^b .

Bereken a en b.

Toon aan dat er sprake is van afnemende groei.