| |
© h.hofstede (h.hofstede@hogeland.nl)
|
| 1. |
examenvraagstuk HAVO Wiskunde
B, 1994. |
| |
|
|
|
| |
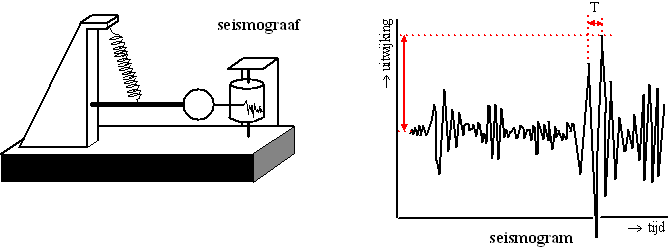
Aardbevingen worden geregistreerd met
een seismograaf, die de aardbevingsgolven weergeeft in een
seismogram. Zie de figuren hieronder. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Verspreid over de aarde staan veel
seismografen opgesteld. De uitwijking van een seismograaf hangt af
van de afstand van dit instrument tot de plaats aan de oppervlakte
van de aarde waar de beving het eerst optreedt. Deze plaats noemt
men het epicentrum van de aardbeving.
Om aardbevingen met elkaar te kunnen vergelijken gebruikt men
seismogrammen die op een afstand van 100 kilometer van het
epicentrum zijn gemaakt (standaardseismogrammen).De kracht van
een aardbeving wordt meestal uitgedrukt in een getal op de schaal
van Richter. Bij deze schaal wordt de logaritme (met grondtal 10)
gebruikt van de grootste uitwijking die in het seismogram voorkomt.
Als de maximale uitwijking van de seismograaf tien keer zo groot
wordt, dan neemt de kracht op de schaal van Richter met één toe.
De aardbeving in Nederland op 13 april 1992 had een kracht van
5,50 op de schaal van Richter. De kracht van de aardbeving in 1960
in Chili was 8,42. Van beide bevingen is in de
standaardseismogrammen de grootste uitwijking gemeten. |
| |
|
|
|
| |
a. |
Bereken de verhouding tussen
deze twee grootste uitwijkingen. |
| |
|
|
|
| |
Als op een bepaald
waarnemingsstation een seismogram gemaakt is en je weet de plaats
van het epicentrum, dan kun je met de volgende formule de kracht van
de aardbeving bepalen: |
| |
|
|
|
| |
R = log(A/T)
+ 1,66 • log D + 3,30
Hierin is: |
 |
| |
|
|
| |
R |
de kracht van de aardbeving,
uitgedrukt in een getal op de schaal van Richter. |
| |
A |
de grootste uitwijking in
het seismogram in mm (1
mm = 0,001 mm). A is aangegeven in de
figuur bovenaan deze opgave |
| |
T |
de tijd in seconden van de
trilling met de grootste uitwijking; ook T is in de figuur bovenaan
deze opgave weergegeven. |
| |
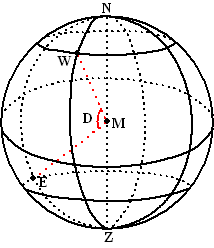
D |
de grootte in graden van de
hoek tussen de verbindingslijnstukken ME en MW. M is het middelpunt
van de aarde, E is het epicentrum en W is de plaats van het
waarnemingsstation. Zie de figuur hiernaast. |
| |
|
|
|
| |
Uit de formule volgt
inderdaad dat de kracht op de schaal van Richter met 1 toeneemt als
de maximale uitslag van de seismograaf tien keer zo groot wordt (bij
dezelfde T en D) |
| |
|
|
|
| |
b. |
Toon dit aan. |
|
| |
|
|
|
| |
Van de Chileense aardbeving
in 1960 werd in De Bilt een seismogram opgenomen. De trillingen
gaven daar een maximale uitwijking van 1000 mm;
de trillingstijd bedroeg 20 seconden. Na invulling van D werd R =
8,42 gevonden. Voor de omtrek van de aarde nemen we 40000 km. |
| |
|
|
|
| |
c. |
Bereken de afstand over de
aardbol tussen De Bilt en het epicentrum in Chili in honderden
kilometers. |
| |
|
|
|
| |
Niet alleen in De Bilt, maar
ook in andere plaatsen werd in 1960 een seismogram van de Chileense
aardbeving opgenomen. Op al die plaatsen berekende men dat de kracht
van de aardbeving 8,42 was.
Hoewel A, T en D van plaats tot plaats verschilden, gaf de
formule voor R steeds 8,42 als resultaat.
Voor deze aardbeving bestaat dus het volgende verband tussen A, T en
D: |
| |
|
|
|
| |
8,42 = log(A/T) + 1,66 • log
D + 3,30 |
| |
|
|
|
| |
d. |
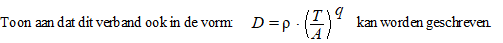 |
| |
|
Bereken p en q
in 2 decimalen nauwkeurig. |
| |
|
|
|
| 2. |
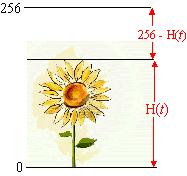
examenvraagstuk
VWO, Wiskunde A, 1984. Onderstaande tabel geeft de gemiddelde
hoogte aan van een bepaald veld zonnebloemen op verschillende
tijdstippen na het ontkiemen. De gemiddelde maximale hoogte die deze
zonnebloemen bereiken is 256 cm. |
| |
|
|
|
| |
| aantal weken |
hoogte in cm |
2
4
6
8
10
12 |
36
98
170
228
251
255 |
|
 |
| |
|
|
|
| |
t is de tijd in weken
na het ontkiemen.
H(t) is de gemiddelde hoogte van deze zonnebloemen in cm op
het tijdstip t. |
| |
|
|
|
| |
a. |
Onderzoek of er sprake is
van lineaire groei, exponentiële groei of geen van beide. |
| |
|
|
|
| |
b. |
Teken met behulp van
de gegevens in de tabel de grafiek van de functie: |
| |
|
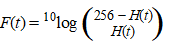 |
| |
|
|
| |
c. |
Toon aan dat er een
eerstegraads functie is die de functie F redelijk benadert en geef
het bijpassende functievoorschrift. |
| |
|
|
|
| |
d. |
Leid uit de resultaten van
b. en c. een functievoorschrift van H als functie van de tijd af. |
| |
|
|
|
| 3. |
examenvraagstuk
VWO, Wiskunde A, 2015.
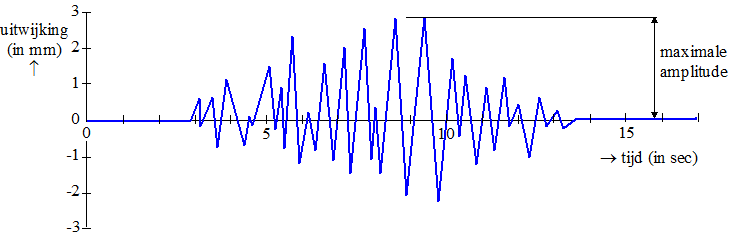
De Amerikaan Charles Richter gebruikte seismogrammen om de
magnitude (kracht) van een beving te kunnen bepalen. In de
figuur zie je een voorbeeld van een seismogram. In dit seismogram
zie je de gemeten trillingen van de aarde als uitwijkingen in mm. De
grootste uitwijking in het seismogram heet de maximale amplitude.
|
| |
|
|
|
|
 |
| |
|
|
|
| |
Om de magnitude van
een beving te bepalen, gebruikt men de formule van Richter. Hier staat een vereenvoudigde versie daarvan: M = log(A)
+ 3
In deze formule
is M de magnitude en A de maximale amplitude in mm.
Uit de formule blijkt, dat als de maximale amplitude A tien keer zo
groot wordt, de magnitude met 1 eenheid toeneemt. |
| |
|
|
|
| |
a. |
Toon met behulp
van de rekenregels voor logaritmen aan dat log(10A) + 3 altijd
1 groter is dan log(A) + 3. |
| |
|
|
|
| |
Met de formule
M = log(A) + 3 kan M berekend worden als A bekend is.
Men kan echter ook A berekenen als M bekend is. Dat kan met de
formule A = 0,001 • 10M.
Deze laatste formule is af te leiden uit de formule M = log(A) + 3.
|
| |
|
|
|
| |
b. |
Toon dit aan. |
| |
|
|
|
| 4. |
examenvraagstuk
HAVO wiskunde B, 2016-I |
| |
|
|
|
| |
Het verband tussen de lengte van karperlarven en hun
gewicht kan beschreven worden met een formule van de vorm:
G = 0,014 •
Lb
met 0,2 ≤ L ≤ 1,9
Hierin is L de lengte in centimeter, G
het gewicht in gram en b een constante.
Een karperlarve van 1,9 cm weegt ongeveer 0,25 g. |
| |
|
|
|
| |
a. |
Bereken
b
met behulp van deze gegevens.
Rond je antwoord af op één
decimaal. |
| |
|
|
|
| |
Voor volwassen karpers geldt de formule:
G = 0,014 • L3,13 met 10
≤ L ≤ 94
Hierin is L weer de lengte in centimeter en G het
gewicht in gram. |
| |
|
|
|
| |
b. |
Bereken hoeveel keer zo zwaar een volwassen karper
van 94 cm is in vergelijking met een volwassen karper van 10 cm.
Rond je antwoord af op honderdtallen. |
| |
|
|
|
| |
De formule G = 0,014 • L3,13
is te herleiden tot een formule van de vorm log(G) =
p + q • log(L) . |
| |
|
|
|
| |
c. |
Bereken de waarden van p en q. Geef
beide waarden in twee decimalen nauwkeurig. |
| |
|
|
|
| |
|
|
|
| 5. |
examenvraagstuk HAVO Wiskunde
B, 2017-I. |
| |
|
|
|
| |
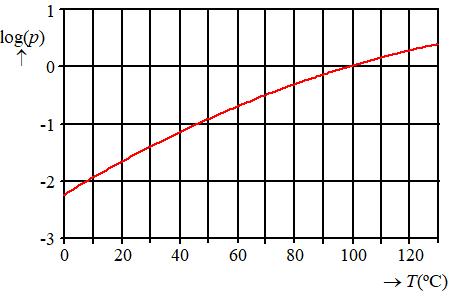
Het kookpunt van water is de temperatuur waarbij
water gaat koken.
Het kookpunt T is afhankelijk van de luchtdruk p met
p in bar en T in °C.
In de figuur is het verband tussen log(p)
en T weergegeven. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Onder normale omstandigheden is de luchtdruk op
zeeniveau 1,0 bar en is het kookpunt van water bij deze luchtdruk
100 °C.
Op de top van Mount Everest is de luchtdruk 0,31
bar. Hierdoor is het kookpunt van water op de top van Mount Everest
een stuk lager dan op zeeniveau. |
| |
|
|
|
| |
a. |
Onderzoek met behulp van de figuur bij welke temperatuur water op de top van Mount Everest gaat koken. Geef je antwoord in hele °C nauwkeurig. |
| |
|
|
|
| |
Het verband dat in de figuur is weergegeven, kan
benaderd worden met de formule: |
| |
|
|
|
| |
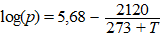 |
| |
|
|
|
| |
Hierin is p de luchtdruk in bar en T
het kookpunt van water in °C.
Op zeeniveau, bij een luchtdruk van 1,0 bar, kookt
rijst in water bij een temperatuur van 100 °C. Als de rijst in een
hogedrukpan wordt bereid onder dezelfde omstandigheden, maar bij een
temperatuur van 130 °C, is de rijst sneller gaar als gevolg van de
hogere druk. |
| |
|
|
|
| |
b. |
Bereken de druk in bar in een hogedrukpan als de
rijst aan het koken is. Geef je antwoord in bar in één decimaal
nauwkeurig. |
| |
|
|
|
| |
In de gegeven formule is log(p)
uitgedrukt in T. |
| |
|
|
|
| |
c. |
Druk T uit in p. |
| |
|
|
|
| 6. |
Examenvraagstuk
VWO Wiskunde A, 2017-I |
| |
|
|
|
| |
Een veelgehoorde bewering is dat het hart van
zoogdieren gedurende hun leven ongeveer een miljard keer slaat. We
gaan dat in deze opgave onderzoeken.
Naar aanleiding van deze bewering kan een formule
voor het verband tussen de hartslag en de levensverwachting
opgesteld worden: H = 1900/L
Hier is L de levensverwachting (in jaren) en
H de hartslag (in slagen per minuut). |
| |
|
|
|
| |
a. |
Toon aan dat deze formule uit de
veelgehoorde bewering volgt. |
| |
|
|
|
| |
Bij controle blijkt dat er dieren zijn waarvoor de
formule ongeveer klopt, maar ook dieren waar de formule helemaal
niet voor klopt, zoals de aap en de muis. In werkelijkheid is het
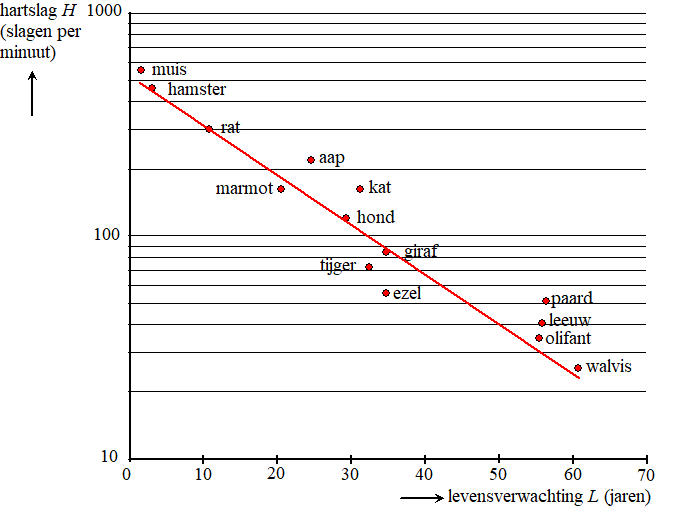
verband anders. In de figuur is de hartslag van een aantal soorten
zoogdieren uitgezet tegen hun levensverwachting. Langs de verticale
as is een logaritmische schaalverdeling gebruikt. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
De punten die de hamster en de walvis weergeven,
liggen nagenoeg op de getekende rechte lijn. De walvis heeft een
levensverwachting van 60 jaar en een hartslag van 25 slagen per
minuut. De hamster heeft een levensverwachting van 3 jaar en een
hartslag van 450 slagen per minuut.
Het verband tussen H (de hartslag in slagen
per minuut) en L (de levensverwachting in jaren) is (bij
benadering) exponentieel en is dus te schrijven als:
H = b •
gL
Uit de grafiek volgt dat b bij
benadering 520 is en g bij benadering 0,95. |
| |
|
|
|
| |
b. |
Bereken met behulp van de gegevens van de hamster en
de walvis g in drie decimalen en b in gehelen. |
| |
|
|
|
| |
Met de formule H = 520 • 0,95L
kun je de hartslag berekenen als je de levensverwachting weet.
Logischer is het om de levensverwachting te berekenen als je van een
zoogdier de hartslag gemeten hebt.
Daarom willen we de formule H = 520 • 0,95L
herleiden tot de vorm: L = a • log(H) +
b |
| |
|
|
|
| |
c. |
Voer deze herleiding uit. Geef a
en b in 2 decimalen nauwkeurig. |
| |
|
|
|
| 7. |
Examenvraagstuk
VWO Wiskunde A, 2022-I
Uit onderzoek
is bekend dat mensen met een hoog inkomen gemiddeld langer leven dan
mensen met een laag inkomen. Het is dan ook niet verwonderlijk dat
de levensverwachting in landen met een hoog gemiddeld inkomen per
persoon doorgaans hoger is dan in landen met een laag gemiddeld
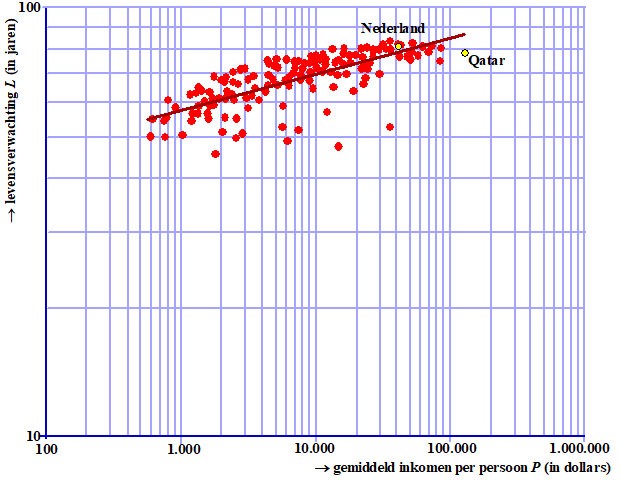
inkomen per persoon. In onderstaande figuur is voor een groot aantal
landen de levensverwachting uitgezet tegen het gemiddelde inkomen
per persoon. Hierbij stelt iedere stip een land voor. Op de
horizontale as staat het gemiddelde inkomen per persoon P (in
dollars) en op de verticale as de levensverwachting L (in
jaren). Alle gegevens gaan over 2012. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
In deze figuur
heeft zowel de horizontale als de verticale as een logaritmische
schaalverdeling. Ook is er een trendlijn toegevoegd die het verband
tussen gemiddeld inkomen per persoon en levensverwachting benadert.
Met een gemiddeld inkomen per persoon van $128722 is Qatar het land
met het hoogste gemiddelde inkomen per persoon ter wereld. Toch was
de levensverwachting daar in 2012 lager dan je volgens de trendlijn
mag verwachten. |
| |
|
|
|
| |
a. |
Bereken met
behulp van schattingen in de grafiek hoeveel procent lager dit is.
Geef je antwoord als een geheel getal. |
| |
|
|
|
| |
De trendlijn in
de figuur is een rechte lijn, dus er bestaat een lineair verband
tussen
log(L) en log(P).
Dit verband ziet er als volgt uit:
log(L) = 0,084 • log(P) + 1,509
Je kunt deze formule ook schrijven als een machtsverband.
Dat verband ziet er dan als volgt uit: L = 32,28 • P0,084 |
| |
|
|
|
| |
b. |
Laat zien hoe
de tweede formule uit de eerste formule is af te leiden. |
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|