Vergelijkingen met logaritmen.

© h.hofstede (h.hofstede@hogeland.nl)
   
Eerder hebben we al gezien hoe je logaritmen kunt gebruiken om exponentiële vergelijkingen op te lossen. Daarin bleek dat glogx een manier is om gx uit een vergelijking weg te krijgen. 
Het kan natuurlijk ook voorkomen dat er in een vergelijking juist logaritmen stáán.

Die kun je dan als volgt oplossen:
   
• Maak de grondtallen gelijk
     
 
 
   
• Neem de logaritmen samen met de rekenregels voor logaritmen
     
    Daarvoor hebben in ons repertoire:
gloga + glogb = glog(ab)  en  gloga - glogb = glog(a/b)  en  glogan  = n • glog(a)
   
• Isoleer de logaritme, en laat die vervolgens verdwijnen door "tot-de-macht- te nemen"
     
    Dat gaat met  glogx = a  ⇔  x = ga
     

Nou, daarmee moet het lukken......
   
Voorbeeld 1:   Los op:  2 • 3logx + 1/3log(2x) = 4

Oplossing:
 
Soms kan het eenvoudiger....
   
Als je van de vergelijking kunt maken  loga = logb  dan kun je direct stellen dat a = b zonder dat je al die moeite moet doen met er eerst één logaritme van maken en zo.Kijk maar:

Voorbeeld 2.  Los op:   2log(x - 12) = 4logx

Oplossing:
Daaruit volgt direct  x - 12 = x1/2   ⇒   (x - 12)2 = x  ⇒   x2 - 24x + 144 = x  ⇒  x2 - 25x + 144 = 0  
⇒  (x - 16)(x - 9) = 0  ⇒ x = 16  ∨  x = 9
Controle levert op dat alleen x = 16 een goede oplossing is.
   
Denk om het domein!
   
Bedenk jezelf goed zodra je "log"  in een opgave ziet staat, dat logaritmen alleen bestaan voor waarden groter dan nul!
 

glogx  bestaat alleen voor  x > 0
 
Dat betekent dat je al je antwoorden moet controleren!
Neem bijvoorbeeld:

Voorbeeld 3.  Los op:   2log(x2 - 6) = 2logx
Daaruit zou volgen dat  x2 - 6 = x  ⇒   x2 - x - 6 = 0  ⇒  (x - 3)( x + 2) = 0   ⇒   x = 3  ∨  x = -2
Maar voor x = -2 bestaat  2logx  helemaal niet!!!!
De enige oplossing is daarom x = 3.
   
Ongelijkheden.
   
Ook bij ongelijkheden moet je er goed om denken dat logaritmen alleen bestaan voor waarden groter dan nul. (Netter gezegd: het domein van de functie  f(x) = glogx   is  〈0, →〉 )

Voorbeeld 4.   Los op:   5log(2x - 7)  ≤  1

Oplossing:
Eerst lossen we op  5log(2x - 7) =  1
Dat geeft  2x - 7 = 51 = 5   ⇒  x = 6
Nu kun je één van de volgende twee dingen doen:

• Schets de grafiek van y = 2log(2x - 7) en lees daaruit af voor welke
x-waarden de grafiek onder de lijn y = 1 ligt. De verticale asymptoot van de grafiek zit bij x = 3,5.

• Maak een tekenbeeld zoals hieronder en  kijk door in te vullen in welke gebieden 5log(2x - 7) kleiner dan 1 is. Vanwege het domein bestaat dit tekenbeeld alleen voor x > 3,5.
 
 

Beide methodes leveren (uiteraard) hetzelfde antwoord op:    〈3.5 , 6 ]
       
Genoeg voorbeelden, nu zélf!
   
  OPGAVEN
   
1. Los algebraïsch op:
       
  a. 1 + 4logx = 31/2 - 2 • 4log(2x)

  2 

d. 1/2 • 3logx = 3logx - 3log5

  25 

  b. 0,5logx = 2 - 3 • 4logx
16  
e. 2 • logx = 1 + log(x + 20)

  20 

  c. 0,2log(x2 - x) = 5log(1/x)

  2 

f. 7logx = 1 +  49log(x - 10)

14 ∨ 35
             
2. Los algebraïsch op:
             
  a. 2 + 3log(6 - x) ≤ 5

[-21,6〉
d. 2log(x - 4) ≥  2log(20 - 2x)

〈4, 8]
  b. 5 - 2logx > 4

〈0, 2〉
e. 4 + 2 • 0,5log(5 - x) > 0

〈1,5〉
  c. 0,5log(2x - 4) - 2 > 0

〈2,21/8〉
f. 2log(x - 4) ≤  5 +  0,5logx

〈4,8]
             
3. De schaal van Richter

Om de kracht (de magnitude) van aardbevingen aan te geven wordt de schaal van Richter gebruikt. Richter definieerde een aardbeving met magnitude 3 als een aardbeving die op een Wood-Anderson seismograaf een uitwijking van 1 mm opwekt op een afstand van 100 km. Verder geeft elke toename van 1 magnitude een 10 keer zo grote uitwijking (op 100 km afstand).
De formule  M = 3 + log(u) past bij deze schaal.  (M in magnitude, u in mm op 100 km afstand)
       
  a. Leg duidelijk uit waarom de formule inderdaad klopt met de gegevens erboven.
       
  b. Welke uitwijking heeft een aardbeving die een magnitude van 2,4 mm geeft? Geef een algebraïsche berekening.
     

0,251 mm
 
De band Rage Against The Machine heeft op Pinkpop 1994 door middel van hun muziek zoveel mensen aangespoord om te springen en stampen dat het een lichte aardbeving (1,0 op de Schaal van Richter) veroorzaakte. Hetzelfde gebeurde op Pinkpop 1998 tijdens een optreden van Primus.
Toen werd er 1,2 op de schaal van Richter gemeten en hiermee werd het record van Rage Against The Machine overgenomen.
     
  c. Hoeveel keer zo groot zal de uitwijking op een seismograaf op 100 km afstand zijn bij dit nieuwe record vergeleken met het eerdere record?
     

1,58 keer
  Proefondervindelijk heeft men berekend dat iedere toename met één magnitude-eenheid overeenkomt met een 30-voudige verhoging van de vrijgekomen energie die in de vorm van seismische trillingen optreedt. De hoeveelheid energie die vrijkomt bij een beving van magnitude 7 is dus 900 maal (30 x 30) zo groot als die welke vrijkomt bij een beving van magnitude 5.
Bij een magnitude van 1 hoort een energie van ongeveer 990000 J (eenheid Joule).
       
  d. Geef een formule voor de vrijkomende energie E als functie van de magnitude M.
     

E = 33000 • 30M
  De energie die bijvoorbeeld vrijkomt wanneer een massa van 1 ton vanaf 100 meter hoogte op de grond valt is te vergelijken met de sterkte van een beving met magnitude 1.
       
  e. Twee zulke massa's van 1 ton zullen vanaf 100 meter hoogte ook twee keer zoveel energie opleveren.
Welke uitwijking zal dat geven op een seismograaf op 100 km afstand?
     

0,016 mm
       
4. Biologen gebruiken voor het aantal diersoorten (n) in een gebied met oppervlakte A de formule  n = k • logA
Daarin is k een constante.
In een bos van 400 km2  leven ongeveer 3500 diersoorten.
Een deel van het bos wordt gekapt, en daardoor leven er na afloop nog maar 2800 soorten. Hoeveel procent van het bos is dan gekapt?
     

69,8%
       
5. Ontzouting ("desalinatie") is een proces om van zout water zoet water te maken. De hoeveelheid zoet water (Z in m3) die in een bepaalde tijd t (in uren) na opstarten kan worden geproduceerd door een ontzoutingsinstallatie voldoet aan:   Z(t) =  1 +  1,14log(pt + 0,88).
Daarin is p een constante, afhankelijk van de installatie.
       
  a. Leg uit hoe je de constante 0,88 zelf zou kunnen berekenen.
     

t = 0 invullen
  b. Een bepaalde installatie produceert in 2 uur 17 m3 zoet water. Hoe lang zal deze installatie erover doen om in één keer 25 m2 zoet water te produceren?
     

6,15 uur
  Als men de installatie stil legt en de filters en pompen schoonmaakt (dat kost 3 uur) kan men daarna opnieuw opstarten.

Een bepaalde installatie heeft p = 4.
       
  c. Deze installatie moet 50 m3 zoet water produceren. Dat kan men doen door in één keer door te werken, maar ook door na elke 3 uur draaien de installatie schoon te maken.
Hoeveel tijdwinst geeft deze tweede methode uiteindelijk?
     

140,85 uur
. d. Als men de installatie (met p = 4)  12 uur laat draaien en men maakt ergens tussendoor 3 uur schoon, hoeveel zoet water kan men dan maximaal in deze 15 uur produceren?
     

51,06 m3
       
6. Het verband tussen de leeftijd L van een bacteriekolonie (in dagen) en de oppervlakte A (in cm2) wordt gegeven door: 
L(A) =  1,5log(50A - 24)

       
  a. Voor welke oppervlaktes geldt deze formule?
       
  b. Een bacteriekolonie heeft oppervlakte 8 cm2. Bereken de leeftijd in maanden nauwkeurig.
       

6,94 dagen
  c. Bereken algebraïsch de oppervlakte van een 10 dagen oude bacteriekolonie.
       

163 cm2
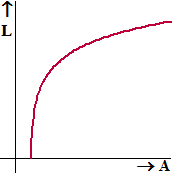
  d. Hiernaast zie je de grafiek van L(A). Met de vorm van de grafiek kun je beredeneren of een kolonie steeds sneller gaat groeien of juist steeds langzamer. Leg duidelijk uit welk van beiden het geval is.
         
7. Gegeven is de functie:   f(x) = 3log(x + 4) - 1/3 log(5 - x)
         
  a. Voor welke waarden van x bestaat f(x)?
       

 〈-4, 5〉

  b. Los op:  f(x) = 3log8
       

4 en -3
  c. Voor welke waarde van a heeft de vergelijking  f(x) = 3loga  precies één oplossing?
       

20,25
8. Gegeven is de functie:   f(x) = √(xlog4 + 4logx - 2)
         
  a. Voor welke waarden van x bestaat deze functie?
       

x > 1
  b. Toon aan dat voor  x > 4   geldt: 
   

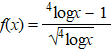9. Examenvraagstuk HAVO Wiskunde B, 2004.

De snelwegen in Nederland zijn voornamelijk asfaltbetonwegen.
De meest voorkomende zijn de dichte asfaltbetonwegen (DAB-wegen) en de zeer open asfaltbetonwegen (ZOAB-wegen).
Voor zulke wegen is een verband op te stellen tussen de snelheid v van het verkeer en het geluidsniveau D van het verkeer.Hierbij is v in km/uur  en  D in dB (decibel)

Voor ZOAB-wegen geldt bij benadering de volgende formule:  D = 28 • log(v) + 16
Een geluidsniveau van 20 dB of lager kun je niet meer horen. Een geluidswal vermindert het geluidsniveau met ongeveer 43 dB. Aan de ene kant van de geluidswal loopt een ZOAB-weg en aan de andere kant wonen mensen.
         
  a. Bereken bij welke snelheid de bewoners achter de geluidswal iets van het verkeer beginnen te horen.
Geef je antwoord in gehele kilometers per uur.
       

48 km/uur
  Voor DAB-wegen geldt voor het verband tussen v en D bij benadering de formule: D = 36•log(v) + 4
         
  b. Bereken algebraïsch bij welke snelheden van het verkeer het geluidsniveau op een ZOAB-weg meer dan 3 dB lager is dan op een DAB-weg.
       

vanaf 75 km/uur
  Een auto wordt op een ZOAB-weg ingehaald door een auto van het zelfde type, die twee keer zo snel rijdt.
         
  c. Onderzoek algebraïsch het verschil van de geluidsniveaus van beide auto's.
       

8,4 dB
         
10. Examenvraagstuk VWO Wiskunde A, 2005.
   
  In de jaren vijftig deed de Amerikaan D.L. Gerlough onderzoek naar de voetgangersveiligheid van wegen. Als er veel verkeer overeen weg gaat, is er voor voetgangers weinig gelegenheid om veilig over te steken.
Daarom stelde Gerlough de zogenaamde 'veilige norm' op. Een weg voldoet aan deze veilige norm wanneer er zich gemiddeld elke minuut een gelegenheid voordoet om veilig over te steken. Dat lukt alleen als het aantal auto's dat per uur passeert onder een maximum blijft. Dit maximum geven we hier aan met Nmax en is afhankelijk  van de breedte van de weg. Bij een brede weg duurt het oversteken langer dan bij een smalle weg. Voor wegen die voldoen aan de veilige norm betekent dit dat er bij een brede weg per uur minder auto's mogen passeren dan bij een smalle weg. Gerlough kwam tot de volgende formule:
         
 

         
 

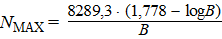In deze formule is B de breedte van de weg in meters.

Vanzelfsprekend is deze formule een model van de werkelijkheid. Met behulp van dit model kunnen we enig inzicht krijgen in de veiligheid bij de aanleg van wegen.

Een weg is 5,40 meter breed. Tijdens de spits passeren 1740 auto's per uur.
         
  a. Voldoet deze weg aan de veilige norm? Licht je antwoord toe.
       

Nee, 1605
  De formule van Gerlough heeft alleen betekenis als Nmax positief is.
         
  b. Bereken voor welke waarden van B dit het geval is. Geef je antwoord in centimeters nauwkeurig.
       

0 < B < 5998
  Een weg waarover volgens de veilige norm per uur maximaal 1648 auto's mogen passeren, wordt 0,50 meter smaller gemaakt. Dit heeft tot gevolg dat het maximum aantal auto's dat per uur mag passeren groter wordt.
         
  c. Bereken hoeveel auto´s er per uur méér mogen passeren in de nieuwe situatie
       

196
         
       
   

© h.hofstede (h.hofstede@hogeland.nl)