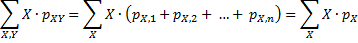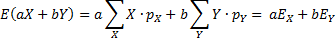© h.hofstede (h.hofstede@hogeland.nl)

Lineaire combinaties van twee stochasten.
       
In een eerdere les hebben we al bekeken wat er gebeurt met het gemiddelde en met de standaarddeviatie als we kansvariabelen bij elkaar optellen. Daar kwam trouwens uit:
 

Esom = E1 + E2 + ...
σsom2 = σ12 + σ22 + ...
       
Maar ja, een aanname daarbij was wél dat die variabelen onafhankelijk van elkaar waren!
Deze les zullen we nader gaan bestuderen wat er nou gebeurt als dat laatste niet zo is.

Een lineaire combinatie.

Stel dat we twee kansvariabelen X en Y hebben en we maken daarvan een nieuwe variabele W = aX + bY   (a en b zijn twee constanten). Wat is dan het verband tussen het gemiddelde en de standaarddeviatie van W en die van X en Y?

Daarvoor moeten we terug naar de definities van gemiddelde en standaarddeviatie.

Eerst maar het gemiddelde....

E(aX + bY) = Σ (aX + bY) • pxy  =  Σ(aX • pxy) + Σ(bY • pxy)   
(als er niets staat bedoel ik de som over alle x en y).
=  aΣX • pxy  + bΣY • pxy  
Maar die beide sommen kunnen we splitsen in een som over X en een som over Y. Neem bijvoorbeeld de eerste som:

We hebben eerst over Y gesommeerd. Maar al die pXY (allemaal bij dezelfde X uitgerekend, voor alle mogelijke waarden van Y) zijn samen precies gelijk aan pX . 
Dat geeft :

       
Dan de standaarddeviatie....
       
He noteert wat handiger als we werken met de variantie (Var) in plaats van de standaarddeviatie. Die variantie is gelijk aan σ2  en dat scheelt bij het noteren een boel wortels.
De variantie   is gelijk aan de gemiddelde kwadratische afwijking:
       
Var(aX + bY) = Σ((aX + bY) - (aXG + bYG))2 • pXY  
=  Σ((aX - aXG) + (bY - bYG))2 • pXY 
=  Σ ((aX - aXG)2 + 2(aX - aXG)(bY - bYG) + (bY - bYG)2 ) • pXY
=  Σ(aX - aXG)2 • pXY  + 2Σ(aX - aXG)(bY - bYG) • pXY  + Σ(bY - bYG)2 • pXY
Laten we deze drie termen stuk voor stuk bekijken:
Σ(aX - aXG)2 • pXY = a2 • Σ(X - XG)2 • pXY  =  a2 • Var(X)
Σ(bY - bYG)2 • pXY  = b2 • Σ(Y - YG)2 • pXY  = b2 • Var(Y)
Σ(aX - aXG)(bY - bYG) • pXY   = ab •  Σ(X - XG)(Y - YG) • pXY  =  ab • Cov(XY)

Een indrukwekkend resultaat:
Var(aX + bY) = a2 • Var(X) + b2 • Var(Y) + 2ab • Cov(XY)

Samengevat:
       

E(aX + bY) = aE(Y) + bE(Y)
Var(aX + bY) = a2Var(X) + b2Var(Y) + 2abCov(XY)
       
Merk nog even op dat, als X en Y onafhankelijk zijn, de Cov = 0  en dan reduceert deze formule tot het al eerder gevonden resultaat.
       
  OPGAVEN
       
1. Het bruto-inkomen van een groep van 10 echtparen  (in duizenden euro's per jaar) ziet er als volgt uit:
       
 
echtpaar inkomen man
M		 inkomen vrouw
V
1
2
3
4
5
6
7
8
9
10		 10
15
15
10
10
15
20
15
20
20		 5
15
10
10
10
5
10
10
15
10
       
  Er wordt willekeurig een echtpaar uit deze groep gekozen.
       
  a. Bereken het gemiddelde en de standaarddeviatie van het bruto-inkomen van de vrouw en de man.
       
  b. Bereken de covariantie van deze bruto-inkomens
       
  c. Stel dat de man 40% belasting moet betalen en de vrouw 20%.
Bereken dan het gemiddelde totale netto-inkomen van man en vrouw samen, en bereken ook de standaarddeviatie daarvan.
Doe dat op twee manieren:
1.  door een nieuwe kolom van het totale netto-inkomen te maken.
2.  door de antwoorden op vraag a) en b) te gebruiken. 
       
2. De leerlingen van een klas hebben twee proefwerken gemaakt, met de volgende resultaten:
       
 
  gemiddelde standaarddeviatie
1e proefwerk
2e proefwerk
gemiddelde G
gewogen gemiddelde W		 5,0
8,0
?
?		 20
20
?
?
       
  De covariantie van de proefwerkcijfers bleek gelijk te zijn aan  5,0
Bij het gewogen gemiddelde telde het eerste proefwerk 2 keer mee, en het tweede 3 keer.

Bereken de vier vraagtekens uit deze tabel.
       
     

© h.hofstede (h.hofstede@hogeland.nl)