| |
 |
|
Limieten voor x
→ ±∞ |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
| Voor limieten waarbij
x naar oneindig gaat heb je wat andere tactieken nodig dan voor
limieten waarbij x naar een bepaald getal nadert. Oneindig is
namelijk geen getal (al is er wel zo'n "8 op zijn kant" voor
bedacht). Laten we de twee meest voorkomende varianten bekijken.
1. Quotiënt van Polynomen. |
 |
Klinkt goed, toch??
Het betekent niets anders dan: twee functies met machten op elkaar
gedeeld. |
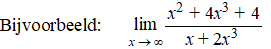 |
| Daar staan duidelijk
twee functies met machten ("polynomen") die op elkaar gedeeld worden
("quotiënt"). |
Met een beetje gezond boerenverstand kom je een heel eind.
Kijk dat zit zo: als x heel heel groot wordt, dan zal de
hoogste macht van x bepalen wat er gebeurt. Die x2
en die 4 en de noemer zijn voor erg grote x volledig te
verwaarlozen ten opzichte van die 4x3 . En op
dezelfde manier is die x in de noemer natuurlijk wel erg groot,
maar toch te verwaarlozen ten opzichte van 2x3. (zelfs
10000x zou nog te verwaarlozen zijn; als x maar groot
genoeg wordt)
Dat betekent dat er voor erg grote x gewoon in de teller 4x3
staat en in de noemer 2x3 dus daar komt 4/2
= 2 uit. |
 |
Oké nu snappen we hoe
het werkt, maar hoe noteren we dat een beetje handig?
Dat gaat als volgt: |
| |
|
|
|
|
Deel alles door de hoogste macht van
x in de noemer. |
|
| |
|
|
|
| In dit voorbeeld
delen we alles door x3 en dat geeft het volgende: |
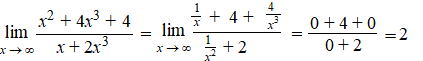 |
| Daarin gaan al die
breuken naar nul, en blijft er over 4/2 = 2.
't Is natuurlijk precies wat die boer hierboven al beweerde, maar zo
staat het een beetje netter genoteerd. |
| |
|
|
|
|
2. Wortelvormen. |
| |
|
|
|
Bij functies met
wortels erin kun je het best zoveel mogelijk machten van x buiten
de wortel proberen te halen.
Daarbij moet je je wel één ding goed bedenken: |
| |
|
|
|
|
|
| |
|
|
|
Dat betekent dat je
voor x → ∞
elke keer √(x2) kunt vervangen door x, maar
voor x → -∞
moet je √(x2) vervangen door -x. Zo'n wortel
moet nou eenmaal positief zijn. Bij bijvoorbeeld √(x4)
heb je dat probleem niet, want dat is gewoon x2 en dat
is altijd positief. maar √(x6) is daarentegen
weer gelijk aan +x3 of -x3
Hier zie je hoe het werkt: |
| |
|
|
|
| Voorbeeld
1. |
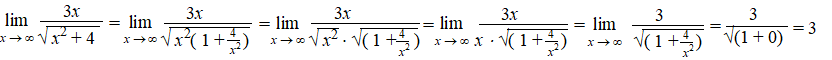 |
| Bij de derde stap is
gebruikt dat √(x2)
= x omdat x → +∞.
Als x naar -∞
was gegaan dan had hier -x moeten staan en dan was de limiet
gelijk geworden aan -3. |
| |
|
|
|
| Voorbeeld
2. |
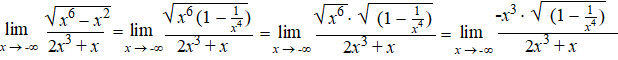 |
| En nu alles nog weer
delen door de hoogste macht van de noemer: |
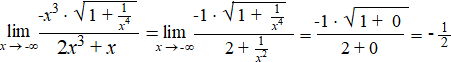 |
| |
|
|
|
|
Oh ja, waarom deden we dit ook
alweer? |
| |
|
|
|
Die limieten van
x naar ±∞ worden
natuurlijk vooral gebruikt om te onderzoeken of een grafiek
horizontale asymptoten heeft. Dat is zo als er uit zo'n limiet
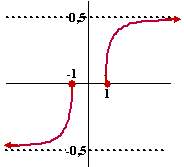
een constant getal komt. Zo zal de grafiek van het laatste voorbeeld aan
de linkerkant naar de lijn y = -1/2 lopen
en aan de rechterkant naar y = 1/2.
In dat vreemde grafiekje hiernaast zie je dat dat inderdaad het geval
is. |
 |
| |
|
|
|
|
Het is niet altijd feest! |
| |
|
|
|
| Natuurlijk komt er
niet altijd zo mooi een constante uit een limiet. Eigenlijk meestal
juist niet! Meestal als x naar oneindig gaat, dan gaat de
y óók naar oneindig. Dat noteren we uiteraard als volgt: |
| |
|
|
|
|
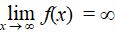 |
| |
|
|
|
| (en natuurlijk kunnen
al die "oneindig" ook worden vervangen door "min-oneindig", maar dat
spreekt intussen voor zich hoop ik) Voorbeeld. |
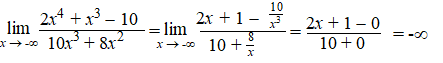 |
| Bij de eerste stap is
gedeeld door x3 (de hoogste macht van de noemer). Je
ziet dat uiteindelijk in de teller 2x + 1 overblijft en dat gaat
naar -∞. |
| |
|
|
|
| |
|
|
|
|
|
|
| 1. |
Bereken algebraïsch de waarde van de volgende
limieten: |
| |
|
|
|
|
|
|
| |
a. |
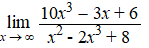 |
|
e. |
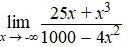 |
|
| |
|
|
|
|
|
|
| |
b. |
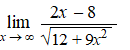 |
|
f. |
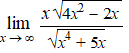 |
|
| |
|
|
|
|
|
|
| |
c. |
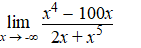 |
|
g. |
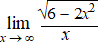 |
|
| |
|
|
|
|
|
|
| |
d. |
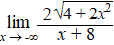 |
|
h. |
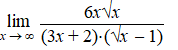 |
|
| |
|
|
|
|
|
|
| 2. |
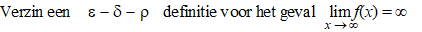 |
| |
|
|
|
|
|
|
| 3. |
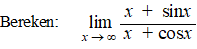 |
| |
Denk daarbij aan de insluitstelling
van de vorige les...... |
| |
|
|
|
|
|
|
| |
|
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|