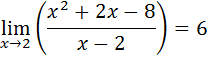limieten


Limieten.	© h.hofstede (h.hofstede@hogeland.nl)

Eerst maar eens twee voorbeelden.

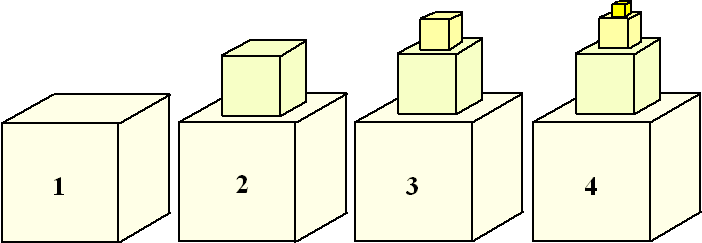
Voorbeeld 1.

Een kunstenaar gaat een kunstwerk maken dat bestaat uit op elkaar gestapelde kubussen.
De onderste kubus heeft ribben van 1.
Daarop stapelt hij een kubus met ribben ¹/₂
Dan eentje met ribben ¹/₄.
En zo gaat hij steeds maar door. Elke kubus heeft ribben die de helft van de vorige kubus zijn. Dat geeft de serie stapels hieronder:

De kunstenaar noemt zijn kunstwerk "The Sky is the Limit", immers als je oneindig veel van zulke kubussen op elkaar stapelt, dan kun je zo hoog komen als je maar wilt. Immers als iets steeds maar groter wordt, dan zal het uiteindelijk elke waarde bereiken......

Maar is dat wel zo?

Hoogste tijd de zaak eens nader te onderzoeken.
Laten we eens een tabel maken met de hoogte H(n) van de stapel als functie van het aantal kubussen (n).
In de tabel hiernaast zie je een aantal waarden.
Daarin lijkt het er helemaal niet op dat die hoogte alle waarden kan aannemen. Het lijkt er meer op dat de hoogste steeds dichter bij 2 komt te liggen.
En dat is ook zo!
Hoe groter je n kiest, des te dichter komt H(n) bij 2 te liggen, maar de waarde 2 zélf wordt nooit bereikt. Het kunstwerk had moeten heten "Two is the Limit" !!

n	H(n)
1	1
2	1,5
3	1,75
4	1,875
5	1,9375
6	1,9688

n	H(n)
7	1,9844
8	1,9922
9	1,9961
10	1,9980
11	1,9990
12	1,9995

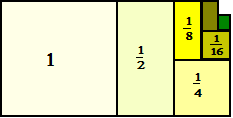
In de wiskunde noemen we zo'n waarde, waar je steeds dichter bij komt een "limiet". Dat die limiet in het verhaaltje hierboven inderdaad 2 is kun je bewijzen met de theorie van meetkundige rijen, en je kunt het ook zien in het plaatje hiernaast. De hele oppervlakte nadert daar naar 2 vierkanten.

We noteren dat als volgt:

Dat spreek je uit als" "De limiet van n naar oneindig van H(n) is gelijk aan 2" en het betekent dus eigenlijk dat, als je n steeds en steeds maar groter maakt, dat dan de waarde van H(n) steeds dichter naar 2 nadert. De waarde 2 zélf wordt nooit bereikt maar je kunt er wel zo dicht als je maar wilt bij in de buurt komen.

Voorbeeld 2.

Dat betekent dus: laat x steeds dichter bij 2 komen en bereken elke keer f(x) en kijk waar die naar naderen.
Luie mensen zullen misschien zeggen "Nou, dan vul ik gewoon 2 direct in de formule in, en wat daar uitkomt, daar zal f(x) dan wel naar toe gaan...." . Maar dat kan niet, want als je x = 2 invult, dan komt er ⁰/₀ uit en dat valt niet te berekenen.
In de tabel hiernaast zie je dat de waarde van f(x) naar 6 toegaat als x naar 2 toegaat.
We noteren dat als:

x	f(x)
1 1,5 1,9 1,95 1,99 1,999 1,9999 1,99999 ....	5 5,5 5,9 5,95 5,99 5,999 5,9999 5,99999 ...

betekent:

Als x nadert naar a, dan nadert f(x) naar b.
"Je kunt zo dicht bij b komen als je maar wilt"

Die laatste regel hierboven hebben wiskundigen vertaald in wat zij noemen de e-d-definitie van een limiet.
Dat ziet er zó uit (niet schrikken):

Mooi hé?

Maar wat staat daar nou eigenlijk?
Je leest het als volgt hardop:
"Voor elke ε > 0 geldt: er is een δ > 0 zodat, als |x - a| < δ, dan is | f(x) - b| < ε "

Ja maar, wat stááááát daar nou?

Laat iemand een willekeurig heel klein getal (ε) kiezen . Alles mag! ("Voor alle ε > 0 geldt:")
Dan kan ik altijd, door een geschikte x te kiezen, dichter dan ε bij de functiewaarde b komen.
Er is altijd een getal vlak bij x = a te vinden ("Er is een δ > 0") zodat de functiewaarde daarvan dichter bij b ligt dan die kleine waarde ε.

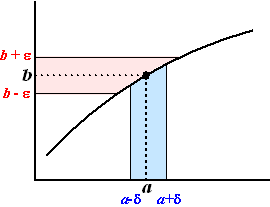
Neem de functie van het laatste voorbeeld hierboven, waarvan de limiet (voor x naar 2) gelijk was aan 6.
Als jij de waarde ε = 0,000001 kiest, dan moet ik proberen een getal vlak bij x = 2 te vinden zodat de functiewaarde ervan dichter dan 0,000001 bij 6 ligt.
Nou dat is makkelijk. Neem bijvoorbeeld δ = 0,0000001. Dan is x - δ = 1,999999 en de bijbehorende functie waarde is f(1,999999) = 5,999999 en dat ligt minder dan 0,00001 van de waarde 6 af.

Met een grafiek ziet dat er zó uit:

Hoe smal je die rode strook ook kiest, je kunt altijd een blauwe strook vinden zodat het stukje grafiek bij de blauwe strook binnen dat bij de rode strook valt.

Voor limieten waar x naar oneindig gaat (zoals in het eerste voorbeeld) zou de definitie er zó uitzien:

Ik hoop dat je begrijpt wat daar staat....

Onderzoek de grootte van de volgende limieten:

-0,2

0,5

-2

0,5

-0,001

Ik beweer dat daar 3 uitkomt, maar mijn buurvrouw gelooft me niet.
Ze kiest ε = 0,001 en ze daagt mij uit δ te vinden waarmee ik op afstand minder dan 0,001 van 3 uitkom als ik de formule toepas.
Welke δ-waarden kan ik nemen om haar te overtuigen?

δ< 0.0002222....

Ik beweer dat daar 4 uitkomt, maar mijn buurman gelooft me niet. (je merkt wel dat mijn buren een niet al te hoge dunk van mij hebben).
Hij kiest ε = 0,0001 en hij daagt me uit een δ te vinden waarmee ik op afstand minder dan 0,0001 van 4 uitkom als ik de formule toepas.
Welke δ-waarden kan ik nemen om hem te overtuigen?

δ > 632,44.......

Bereken achtereenvolgens f(1) en f(0,5) en f(0,1) en f(0,05) en f(0,01) en geef aan de hand van deze waarden een schatting voor de limiet van x naar nul van f(x)

Bereken f(0,000005) en f(0,000001) en f(0,0000005)
Ben je er nog steeds van overtuigd dat je schatting van vraag a) correct is?

Beperkingen van de rekenmachine.

Dat uitrekenen van waarden dichter en dichter bij de limietwaarde gaat helaas niet altijd goed. Dat komt door de beperkingen van onze rekenmachine. Die kan nou eenmaal niet met oneindig grote of kleine getallen rekenen.
Twee voorbeelden.

Hiernaast heb ik een tabelletje staan voor x steeds dichter in de buurt van 0.
Daaruit zul je waarschijnlijk concluderen dat de limiet gelijk is aan 0,25.
En dat is ook zo.
Waarom dan dit voorbeeld?
Nou, als je overijverig (of paranoïde) bent zou je wel eens op het idee kunnen komen om waarden nóg dichter bij nul te gaan bekijken.
Voor de zekerheid....

x
±0,1	0,24984...
±0,01	0,24999...
±0,001	0,25000...

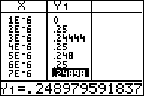
Dat geeft op mijn TI-83 bijvoorbeeld het tabelletje hiernaast, voor waarden van 0,000001 en 0,000002 en 0,000003 enz.
Je ziet dat de waarden dan weer verschillend van 0,25 worden! Het springt een beetje heen en weer.
Gaat die waarde dan toch af en toe weer van 0,25 aflopen?
Gelukkig niet; het zit hem hier in een fout van de GR. Dat komt omdat de waarde van √(x² + 4) - 2 extreem dicht bij nul komt te liggen als x naar 0 gaat. Meer decimalen dan je rekenmachine aankan.

Voorbeeld 2.

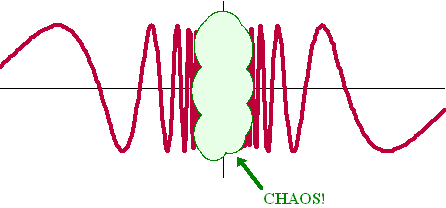
Een tabelletje staat hiernaast.
Nou dat lijkt overduidelijk: daar komt nul uit.
Maar als je per ongeluk probeert x = 0,06 dan vind je een waarde 0,866...
Wat is er aan de hand?
Voor waarden van x = ¹/_n (met n een geheel getal) komt er inderdaad steeds nul uit deze formule. Maar daartussenin niet!
Dat zit hem in de grafiek van y = sin(^π/_x), want die ziet er zó uit in de buurt van nul:

x	sin(^π/_x)
0,1	0
0,05	0
0,01	0
0,001	0
0,0001	0

Dat is een sinusgrafiek met steeds kleinere wordende periode, en die kan je rekenmachine niet tekenen. Dat geeft chaos. De grafiek gaat steeds sneller heen en weer tussen 0 en 1, maar nadert niet naar een bepaalde waarde. Daarom moeten we vaststellen dat er niet zoiets bestaat als "DE" limiet. (in de ε-δ definitie: als je ε < 1 kiest zijn er altijd weer δ's die de boel bederven waarvoor sin^π/_x groter dan ε wordt).