© h.hofstede (h.hofstede@hogeland.nl)
De stelling van Pythagoras.
Pythagoras was een Griek die zo'n 500-600 jaar voor Christus leefde, en die een school runde die zich vooral bezig hield met  GETALLEN. En dat waren in zijn geval alleen maar mooie gehele getallen.
Nou hielden die Grieken helemaal niet zoveel van getallen op zich; ze vonden meetkunde eigenlijk veel en veel interessanter. Daarom probeerden ze zoveel mogelijk om hun ontdekkingen over getallen te vertalen naar meetkundige beweringen.

Pythagoras (of misschien wel één van zijn leerlingen) ontdekte dat er tussen de lengte van de zijden van een rechthoekige driehoek een vast verband bestond.

Als je de zijden a, b, en c noemt, dan geldt:

a2 + b2  = c2
Maakt het nog uit welke je a, b of c noemt?
Jazeker!
Dat zie je al wel aan de formule. Die a en b die kun je vrij met elkaar verwisselen, dat verandert niks aan de formule. Maar die c, die is wel belangrijk.  Die staat alleen en dat is de langste van de drie.
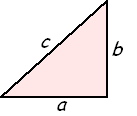
c is de schuine zijde.
Als je niet zeker weet welke dat is:  het is de langste, en hij zit tegenover de rechte hoek.
c is de zijde tegenover de rechte hoek.
a en b zijn de andere twee.
   
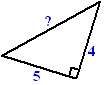
Voorbeeld 1.  Bereken het vraagteken in de figuur hiernaast
Oplossing:
x2 = 42 + 52 = 16 + 25 = 41
Dus x = √41

   
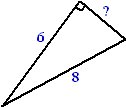
Voorbeeld 2.  Bereken het vraagteken in de figuur hiernaast.
Oplossing:
82 = 62 + x2
64 = 36 + x2
x2 = 28
Dus x = √28.

   
 
  De Pythagoras-aanhangers vertaalden alles het liefst naar meetkundige figuren en de oppervlaktes daarvan in plaats van getallen.
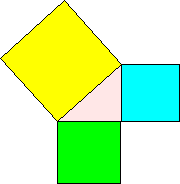
Daarom vertaalden zij de formule a2 + b2 = c2 ook in termen van oppervlaktes.
Een Pythagoreeër zou zich niet druk maken om letters, maar hij zou van de figuur hiernaast simpelweg beweren:
geel = groen + blauw
Ik hoop dat je snapt dat deze bewering in feite dezelfde is als de stelling van Pythagoras   a2 + b2 = c2
Leuk Voorbeeldje!!

Iemand spant een touw over een voetbalveld. Het veld is 100 meter lang en het touw loopt van de ene doelpaal strak over de grond naar de doelpaal aan dezelfde kant van de tegenoverliggende goal. Het touw is dus 100 meter lang. Vervolgens knipt hij op de middellijn het touw door en knoopt er een meter extra touw tussen.
Daardoor is het touw net iets te groot en kan hij het bij de middellijn een stukje van de grond optillen.
Hoe ver?
 
a.  er kan een knikker onderdoor rollen.
b.  er kan een krat bier onderdoor schuiven.
c.  er kan een tafel onderdoor schuiven.
d.  er kan een mens rechtop onderdoor lopen.
e.  er kan een vrachtauto onderdoor rijden.
 
Maak eerst een schatting!
Het halve touw was eerst 50 meter lang, en is nu 50,5 meter lang geworden. Als je het zo ver mogelijk optilt krijg je met dat halve touw een rechthoekige driehoek met een schuine zijde van 50,5 en een rechthoekszijde van 50.
Dan geldt dus:  50,52 = 502 + b2  ofwel b2 = 50,52 - 502 = 50,25.
Dus b = √50,25 ≈ 7,1 meter!   Kortom:  antwoord   e) is het juiste.
   
 
 
OPGAVEN
   
1. Bereken het vraagteken in de volgende driehoeken. Rond je antwoord af op twee decimalen.
       
 

       
     

A: 9,43;  B: 6,00
C: 12,65;  D: 54,15
2. Bereken het vraagteken in de volgende driehoeken. Rond je antwoord af op twee decimalen.
       
 

     

6,32 en 10,15
3. Een driehoek met zijden  10-12-12 heeft dezelfde oppervlakte als een driehoek met zijden  10-13-13.
Bewijs dat!
       
4. In gelijkzijdige driehoek ABC met zijden 12 is M het midden van BC en N is het midden van AM

Bereken de lengte van BN.
     

© h.hofstede (hhofstede@hogeland.nl)