Nog meer haakjes...

© h.hofstede (h.hofstede@hogeland.nl)

((( )( )( ))( ))( )(((( )( ))((((( )( )( )(((((( )( )( )( ))(( )))))))) ( )( )(((( ) ( )(( )( )( )))( )( )(( )((( ))(((( ))))))(( )( )( )( ))( )( ))(( )( )( )( )( )(( )( )(((((((( )))((( )( )( ))( ))( )(((( )( ))((((( )( )( )(((((( )( )( )( ))(( )))))))) ( )( )(((( ) ( )(( )( )( )))( )( )(( )((( ))(((( ))))))(( )( )( )( ))( )( ))(( )( )( )( )( )(( )( )(((((((( )))((( )( )( ))( ))( )(((( )( ))((((( )( )( )(((((( )( )( )( ))(( )))))))) ( )( )(((( ) ( )(( )( )( )))( )( )(( )((( ))(((( ))))))(( )( )( )( ))( )( ))(( )( )( )( )( )(( )( )(((((((( )))((( )( )( ))( ))( )(((( )( ))((((( )( )( )(((((( )( )( )( ))(( )))))))) ( )( )(((( ) ( )(( )( )( )))( )( )(( )((( ))(((( ))))))(( )( )( )( ))( )( ))(( )( )( )( )( )(( )( )(((((((( )))((( )( )( ))( ))( )(((( )( ))((((( )( )( )(((((( )( )( )( ))(( )))))))) ( )( )(((( ) ( )(( )( )( )))( )( )(( )((( ))(((( ))))))(( )( )( )( ))( )( ))(( )( )( )( )( )(( )( )(((((((( )))((( )( )( ))( ))( )(((( )( ))((((( )( )( )(((((( )( )( )( ))(( )))))))) ( )( )(((( ) ( )(( )( )( )))( )( )(( )((( ))(((( ))))))(( )( )( )( ))( )( ))(( )( )( )( )( )(( )( )(((((((( )))((( )( )( ))( ))( )(((( )( ))((((( )( )( )(((((( )( )( )( ))(( )))))))) ( )( )(((( ) ( )(( )( )( )))( )( )(( )((( ))(((( ))))))(( )( )( )( ))( )( ))(( )( )( )( )( )(( )( )(((((((( )))...
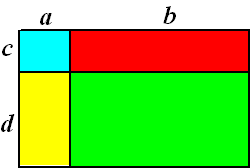
Kijk naar de rechthoek hiernaast. Die is verdeeld in 4 kleinere rechthoeken.
De oppervlakte van die rechthoek kun je op twee manieren gaan opschrijven.

manier 1.

Je zegt gewoon oppervlakte = lengte Χ breedte
In dit geval is de lengte  a + b  en de breedte  c + d
De oppervlakte is dus  O = (a + b) • (c + d)

manier 2.
Je kunt ook zeggen: ik bereken de oppervlakte door de oppervlaktes van de vier kleinere gekleurde rechthoeken apart uit te rekenen en dan die vier getallen bij elkaar op te tellen.
Dan krijg je oppervlakte  O = a • c + a • d + b • c + b • d

(a + b) • (c + d) = ac + ad + bc + bd

Wat gebeurt er nou eigenlijk?  Je moet elk getal binnen dat eerste paar haakjes vermenigvuldigen met elk getal binnen dat tweede paar haakjes. Met onze blokjes-notatie zou dat er zσ uitzien:

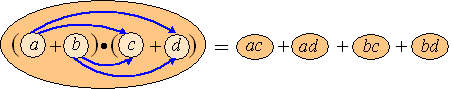Dat enorme blok links is gesplitst in vier kleine blokjes rechts.
•  Denk erom dat in plaats van die a, b, c of d  ook elk ander blokje kan staan.
•  En bedenk verder dat je misschien het antwoord (die 4 kleine blokjes rechts) nog weer eenvoudiger kunt schrijven door blokjes samen te nemen.

voorbeeldjes:

(2x + 3) • (4 + 5x) = 2x • 4 + 2x• 5x + 3 • 4 + 3 • 5x  =  8x + 10x2 + 12 + 15x  = 23x + 10x2 + 12

(4 - 2p) • (5 + p) = 4 • 5 + 4 • p  + -2p • 5 + -2p • p = 20 + 4p - 10p - 2p2 = 20 - 6p - 2p2

1. Schrijf zonder haakjes en zo eenvoudig mogelijk:
a. (x + 4)(x + 5)

x2 + 9x + 20
h. (2 - 3p)(-3p - 2)

9p2 - 4
b. (x + 7)(x - 3)

x2 + 4x - 21
i. (x - 6)(x + 6)

x2 - 36
c. (a - 5)(a - 6)

a2 - 11a + 30
j. (x + y)(2x + 3y)

2x2 + 5xy + 3y2
d. (p + 3)(2p + 2)

2p2 + 8p + 6
k. (2a - 4)(7 - a)

-2a2 + 18a - 28
e. (b - 4)(5 + 3b)

3b2 - 7b - 20
l. (3x - 1)(x + 2) - 5x

3x2 - 2
f. (2k - 2)(k - 4)

2k2 - 10k + 8
m. (2x + 4)(2x - 3) - 4x2

2x - 12
g. (3 - 2h)(3h + 1)

-6h2 + 7h + 3
n. q2 + (-1 - q)(2q + 2) + 4q

-q2 - 2
Speciaal geval 1:  Kwadraat.
Vroeger heb je ooit geleerd dat  "kwadraat = getal keer zichzelf". 
Dus x2 = x • x  en  a2 = a • a.
Nou, het goede nieuws is:  met "blokjes" gaat dat precies zo, overal mee trouwens!

Dus is ook (x - 3)2 = (x - 3) • (x - 3)
Dat kunnen we uitwerken tot  x2 - 6x + 9  (reken het zelf maar na)

(a + b)2 = (a + b)(a + b)
Speciaal geval 2:  Er staat nog mιιr!
Wat gebeurt er als er vσσr zulke blokjes met haakjes nog meer staat?
Neem bijvoorbeeld:  3(x + 2)(x - 4)

Hier staan eigenlijk drie blokjes keer elkaar. 
De oplossing is voor de hand liggend:  combineer eerst twee van zulke blokjes met elkaar, en combineer vervolgens je resultaat met het derde blokje.
De volgorde waarin je dat doet maakt niet uit. Er komt hetzelfde uit als je eerst 3 • (x + 2) uitrekent, dan wanneer je eerst (x + 2)(x - 4) uitrekent,  kijk maar:

   

   

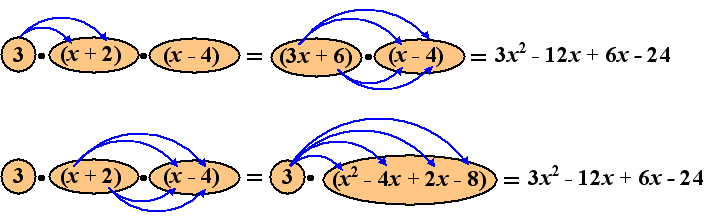ontbinden in factoren

    

som-productmethode
   
OPGAVEN
2. Schrijf zonder haakjes en zo eenvoudig mogelijk:
a. (x + 2)2

x2 + 4x + 4
f. 2 + 4(x - 2)2 

4x2 - 16x + 18
b. (x - 5)2

x2 - 10x + 25
g. 3x(2 + x)2 

3x3 + 12x2 + 12x
c. (6 + 3x)2

9x2 + 36x + 36
h. x2 - (x - 4)2 

8x - 16
d. (2a + b)2

4a2 + 4ab + b2
i. 5x + (1 + 2x)2 + x2

5x2 + 9x + 1
e. 2(x + 1)2

2x2 + 4x + 2
j. p2(2p - 3)2 

4p4 - 12p3 + 9p2
3. Schrijf zonder haakjes en zo eenvoudig mogelijk:
a. (x + 1)(x - 2)(x + 3)

x3 + 2x2 - 5x - 6
c. (x + 4)3

x3 + 12x2 + 48x + 64
b. (a + 2)(b + 3)(a - 2)

a2b + 3a2 - 4b - 12
d. (2p - 3)3

8p3-36p2 + 54p - 27
   
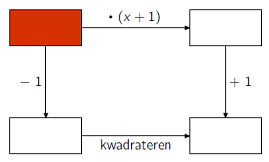
4. Vlaamse Olympiade.

Jeroen schrijft in elk vakje een veelterm in x, verschillend van 0, zodat het schema klopt.

Wat staat er in het gekleurde vakje?
     

x + 3
       

© h.hofstede (h.hofstede@hogeland.nl)