| |
 |
| Werken
met Wortels. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
|
|
|
|
Eerst even iets over de notatie
met wortels.
Ook met wortels zijn blokjes mogelijk. Dat kun je op twee manieren
noteren.
Op de eerste plaats kun je natuurlijk haakjes gebruiken: dat maakt er
automatisch één geheel van. Maar je kunt ook een streep boven het
wortelteken doortrekken. Dit betekent precies hetzelfde: |
|
|
|
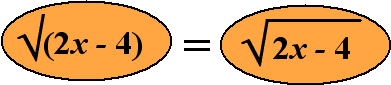 |
|
|
| Het is beide één blokje. |
|
|
Bij het werken met wortels is het
erg belangrijk om in de gaten te houden wat er wel en wat er niet mag.
Er zijn twee hoofdregels: |
|
|
| regel 1: |
Je kunt niet de wortel uit een negatief
getal nemen |
| regel 2: |
De wortel uit een
getal is altijd positief. |
|
|
|
|
| De eerste regel lijkt me vrij
logisch. Je weet dat wortel nemen het omgekeerde van kwadrateren is.
Omdat er uit een kwadraat geen negatief getal kan komen, kan een wortel
van een negatief getal dus niet bestaan. Als je √(-3)
wil uitrekenen dan zoek je het getal dat keer zichzelf -3 oplevert. Maar
dat bestaat niet. Als je een getal keer zichzelf doet komt er altijd een
positief getal uit! Dat kan nooit -3 worden!!! |
|
|
De tweede regel is wat lastiger.
Als je wortel ziet als omgekeerde van kwadraat, dan zeg je dus
bijvoorbeeld √9 = 3 want 32
= 9. Maar ja, dan kun je net zo goed zeggen √9
= -3 want (-3)2 = 9, dat klopt immers óók.
Maar ja, dan zou er uit √9 zowel 3 als -3
kunnen komen.
Dat vinden wiskundigen heel irritant......
Ze willen graag dat er uit elke bewerking (dat noemen ze trouwens een functie)
maar één antwoord komt.
De fabrikant van je rekenmachine vindt dat trouwens ook wel prettig. Het zou
nogal lastig zijn als je √9 intoetst dat er
dan TWEE antwoorden in het venster moeten komen!!
Daarom hebben "we" met elkaar afgesproken dat de wortel van een getal
altijd positief is.
Dus eigenlijk moeten we bovenstaande regels veranderen in een regel en
een afspraak: |
|
|
| regel: |
Je kunt niet de wortel uit een negatief
getal nemen. |
| afspraak: |
De wortel uit een getal is altijd
positief. |
|
|
|
|
|
|
|
|
| rekenen
met wortels |
|
|
|
Kijk wat er gebeurt als we √5
• √3 in het kwadraat nemen:
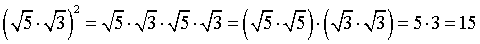
Hier staat eigenlijk:
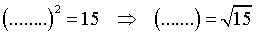
De enige mogelijke conclusie is dat √5 • √3 = √15.
En met letters werkt het natuurlijk precies zo, dat heb je hopelijk
intussen al wel door. |
|
|
|
|
|
|
De regel mag je natuurlijk ook
andersom lezen. Zo kun je bijvoorbeeld zien dat √(4x)
= √4 • √x
= 2√x
En omdat delen wiskundig gezien eigenlijk bijna hetzelfde is als
vermenigvuldigen (delen door 4 is immers vermenigvuldigen met 0,25?) mag
het ook bij delen: |
|
|
|
|
|
|
Maar wat met vermenigvuldigen wél
mag, is met optellen of aftrekken streng verboden. Als er onder de
wortel wordt opgeteld of afgetrokken dan kun je niet vereenvoudigen.
Daar moet je afblijven.
Dat moet je gewoon laten staan.
En toch gaat dat vaak fout. Ik snap dat wel, dat komt doordat we zoveel
met haakjes hebben geoefend. Daar moesten we steeds boogjes maken om ze
weg te werken. Geef toe, dit is wel erg aantrekkelijk om met elkaar te
vergelijken: |
|
|
|
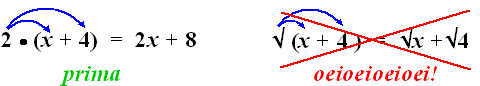 |
|
|
De eerste is goed maar de tweede
is de grootste flauwekul!!!!
Dan krijg je bijvoorbeeld onzin als √2
= √(1 + 1) = √1
+ √1 = 1 + 1 =
2 jaja: dus √2
= 2......???
Trap daar niet in! Zo'n wortel mag je niet verdelen over losse dingen
die er onder staan. |
|
|
|
|
|
|
|
|
|
|
| Iets
buiten de wortel halen. |
|
|
Die regel van √(ab)
= √a • √b
is erg handig, maar je moet er wel mee uitkijken....
Met getallen gaat het meestal wel goed, kijk maar: √(48)
= √(16 • 3) = √16
• √3 = 4√3.
Niks aan de hand.
Geen vuiltje aan de lucht...
Maar met letters kun je wel eens in de problemen komen: √(5x2)
= √5 • √(x2)
=
√5 • x ??????
Lijkt logisch niet?
Maar kijk wat er gebeurt als we bijvoorbeeld nemen x = -2, dan is
5x2 = 5 • 4 = 20.
Met x = -2 staat er dan √20
= √5 • -2
Maar dat KAN NIET KLOPPEN, want
links staat een wortel en die is positief, en rechts staat iets dat
negatief is!!!
Dat kan nooit gelijk zijn!
Wáár oh wáár hebben we een fout gemaakt?
Het zit hem allemaal in die √(x2).
Die is niet altijd gelijk aan x.
Als je een getal in het kwadraat neemt, en daarna er weer de wortel van
neemt, dan hoeft niet het getal zelf er weer uit te komen. Voor
negatieve getallen klopt dat niet. Kijk maar: (-3)2
= 9 maar √(9) = 3
Het zit hem allemaal in die afspraak dat een wortel positief moet zijn.
Dus: √(x2 ) = x
maar x moet wel positief zijn. Als hij negatief is moet je hem
positief maken.
Wiskundigen hebben daar uiteraard weer een notatie voor verzonnen:
|
|
|
|
|
|
|
| En die rechte strepen betekenen
"maak het positief" . |
|
|
|
|
|
|
|
|
| 1. |
Schrijf de volgende wortels zo
eenvoudig mogelijk; zorg dat er een zo klein mogelijk (geheel)
getal onder het wortelteken staat. |
|
|
|
|
|
|
|
|
a. |
√(54) |
|
e. |
√(80) |
|
|
b. |
√(300) |
|
f. |
√(108) |
|
|
c. |
√(56) |
|
g. |
√(252) |
|
|
d. |
√(18) |
|
h. |
√(98) |
|
|
|
|
|
|
|
|
| 2. |
GOED of FOUT? |
|
|
|
|
|
|
|
|
a. |
√(36x) = 6√x |
|
e. |
√x + √x
= √(2x) |
|
| |
|
|
|
|
|
|
|
b. |
√(9 + x) = 3 + √x |
|
f. |
√(4 + x) • √(4
+ x) = 16 + x |
|
| |
|
|
|
|
|
|
|
c. |
√(x)• √(x
+ 1) = √(x2 + 1) |
|
g. |
√(x + x
+ 2x) = 2√x |
|
| |
|
|
|
|
|
|
|
d. |
√(x) + √(2x)
= √(3x) |
|
h. |
√(9x) - √(4x)
- √(x) = 0 |
|
| |
|
|
|
|
|
|
| 3. |
Door de wortels kleiner te maken kun
je de volgende uitdrukkingen veel eenvoudiger schrijven. Doe
dat. |
|
|
|
|
|
|
|
|
a. |
√(28) + √(112) |
|
c. |
√(45) + √(80) |
|
|
b. |
√(50) - √(18) |
|
d. |
√(18) - √(32)
+ √(2) |
|
|
|
|
|
|
|
|
| 4. |
Schrijf de volgende wortels zo
eenvoudig mogelijk: |
|
|
|
|
|
|
|
|
a. |
√(x4) |
|
e. |
√(x2
+ 2x + 1) |
|
|
b. |
√(2x + 7x) |
|
f. |
(x√x)4 |
|
|
c. |
√(x3 +
3x2) |
|
g. |
√(4x2
+ 2x2) |
|
|
d. |
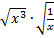 |
|
h. |
√(x2
+ 9) |
|
|
|
|
|
|
|
|
| 5. |
Wat moet er op de stippeltjes staan? |
|
|
|
|
|
|
|
|
a. |
√(3) + √(....)
= √(48) |
|
b. |
√(x) + √(16x)
= √(....) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
| 6. |
Examenvraagstuk VWO
Wiskunde A, 2013.
Voor het berekenen van de lichaamsoppervlakte bij
kinderen worden vooral de volgende twee formules gebruikt: |
| |
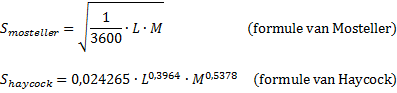 |
| |
|
|
|
| |
In deze formules is S de lichaamsoppervlakte in m2,
L de lichaamslengte in cm en M het lichaamsgewicht in kg.
Om de formules beter met elkaar te kunnen vergelijken is
het handig om de formule van Mosteller in dezelfde vorm te schrijven als
de formule van Haycock.
Schrijf de formule van Mosteller in de vorm S
=
c •
La •
Mb en licht toe hoe
je je antwoord gevonden hebt. |
| |
|
|
|
| 7. |
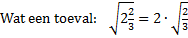 |
| |
| |
|
|
|
| a. |
Toon aan dat dat inderdaad zo is |
| |
|
|
|
| b. |
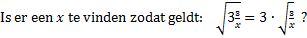 |
|
| |
|
|
|
|
| |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
 |