lengte van een vector


De lengte van een vector.	© h.hofstede (h.hofstede@hogeland.nl)

De lengte van een vector, daar valt niet zoveel spectaculaire wiskunde aan te bedrijven. 't Is eigenlijk alleen maar Pythagoras, meer niet.
Als de kentallen a en b zijn, dan is de lengte √(a² + b²), that's it folks!

De lengte wordt ook wel de norm van een vector genoemd, en meestal genoteerd door de naam van de vector tussen absolute waarde strepen te zetten.

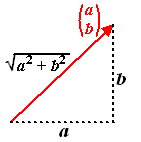Door een vector met een gewoon getal te vermenigvuldigen kun je de lengte ervan veranderen. Dat kun je gebruiken door een vector met een gevraagde lengte te maken.

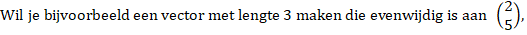dan moet je je eerst bedenken dat die laatste vector lengte √(2² + 5²) = √29 heeft. Dus om die op lengte 3 te brengen moet je hem vermenigvuldigen met ³/_√29.

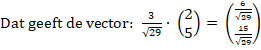Waarom zou je dat in vredesnaam willen?

Een voorbeeld is denk ik het duidelijkst.

Voorbeeld 1.

Geef een vergelijking van de lijn die afstand 3 tot de lijn y = ¹/₂x + 1 heeft.

Met "afstand" wordt hier "kortste afstand" bedoeld, en dat is de loodrechte afstand.
Je kunt dus niet simpel zeggen "Oh, ik schuif hem gewoon 3 omhoog of omlaag en dan krijg ik y = ¹/₂x + 4 of y = ¹/₂x - 2" Wa nt dan krijg je de verticale afstand en niet de loodrechte afstand.

Het kan als volgt wél.
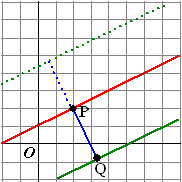
Kies een punt van de lijn, bijvoorbeeld P(2, 2), en maak een vector PQ die loodrecht op de gegeven lijn staat.

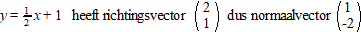De lengte van die normaalvector is √(1² + 2²) = √5 en dat moet worden 3, dus die moet je vermenigvuldigen met ³/₅√5.

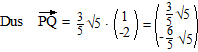Dan is Q het punt (2 + ³/₅√5, 2 - ⁶/₅√5)
De gevraagde lijn heeft vergelijking y = ¹/₂x + b en gaat door dat punt Q.
Dat geeft 2 - ⁶/₅√5 = ¹/₂ • (2 + ³/₅√5) + b ofwel b = 1 - 1¹/₂√5 en de lijn is dus y = ¹/₂x + 1 - 1¹/₂√5.

(merk op dat we één van beide mogelijkheden hebben gevonden, de andere (met die stippellijnen in de figuur) vind je door de normaalvector de andere kant op te nemen, dus met -1 te vermenigvuldigen).

Bewegingen in het platte vlak.

Als het gaat om punten die in het vlak bewegen is het vaak handig om als l van een lijn de tijd t te nemen.
Neem in de volgende voorbeelden steeds aan dat roosterhokjes afmetingen van 1 cm bij 1 cm hebben.

Voorbeeld 2.

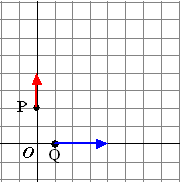
Punt P beweegt met snelheid 2 ^cm/_sec langs de y-as omhoog , en punt Q beweegt met een snelheid van 3 ^cm/_sec langs de x-as naar rechts. Op t = 0 start punt P in het punt (0, 2) en punt Q in het punt (1,0). M is het midden van lijnstuk PQ.
Toon aan dat de punten M op een rechte lijn liggen en geef een vectorvoorstelling van die lijn.

Voor de plaatsvectoren van de oorsprong naar P en Q als functie van de tijd t kun je het volgende opstellen:

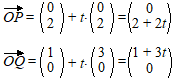M is het midden van die twee, dus moet je het gemiddelde van de x- en de y-coördinaten nemen:

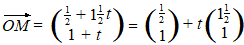Daar is de gevraagde lijn al.

Kijk uit met schuine lijnen! Om die snelheden dan in de goede verhouding te krijgen zou ik er voor zorgen dat de richtingsvectoren van de gebruikte lijnen dezelfde lengte hebben.

Bijna voorbeeld 2 nog een keer.

Punt P beweegt met snelheid 2 ^cm/_sec verticaal omhoog, en punt Q beweegt met een snelheid van 4 ^cm/_sec langs de lijn y = x naar rechtsboven . Op t = 0 start punt P in het punt (2, 4) en punt Q in de oorsprong. M is het midden van lijnstuk PQ.
Toon aan dat de punten M op een rechte lijn liggen en geef een vectorvoorstelling van die lijn.

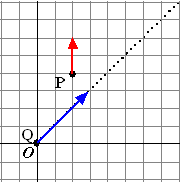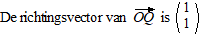Die heeft lengte √2, en dat moet lengte 4 worden, dus moet je vermenigvuldigen met 4/_√2 = 2√2. Dat geeft de volgende plaatsvectoren:

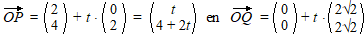Het midden M is weer het gemiddelde van de x-coördinaten en de y-coördinaten:

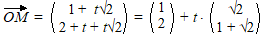Voorbeeld 3.

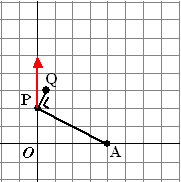
Punt P begint op t = 0 langs de y-as omhoog te bewegen met snelheid 3 ^cm/_sec, met als beginpunt (0,2)
A is het vaste punt (4,0)
Q is een punt rechts van P waarvoor geldt dat PQ loodrecht op AP staat en waarvoor PQ = ¹/₄AP.
Onderzoek de baan van de punten Q.

Op tijdstip t geldt:

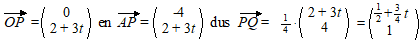Denk erom dat je even controleert dat deze normaalvector inderdaad een punt rechts van P oplevert, dus dat je hem niet per ongeluk de verkeerde kant op hebt genomen. Hier zie je dat direct doordat de y gelijk is aan 1 en dat is positief.

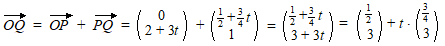De punten Q liggen op de lijn met deze vectorvoorstelling (dat is trouwens de lijn y = 4x + 1, ga dat zelf maar na).

OPGAVEN

1.	De punten P en Q liggen beiden op de lijn y = 3x - 6. Punt P is het punt (8, 18). Punt Q ligt op afstand 10 van P. Geef de coördinaten van Q (er zijn twee mogelijkheden).

2.	De punten P en Q beginnen beiden op t = 0 vanuit de oorsprong te bewegen. Punt P beweegt met een snelheid van 2 ^cm/_sec langs de lijn y = ⁴/₃x naar rechts. Punt Q beweegt met een snelheid van 4 ^cm/_sec langs de lijn y = -⁵/₁₂x omlaag. Geef een formule voor de afstand PQ op tijdstip t.

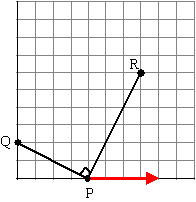
3.	Q is het vaste punt (0, 2). P is een punt dat op t = 0 begint in (4, 0) en dat met een snelheid van 4 ^cm/_sec naar rechts over de x-as beweegt (de roosterhokjes zijn 1 cm). R is een punt met positieve y-coördinaat, zodat QP en PR loodrecht op elkaar staan en waarvoor bovendien geldt PR = 1¹/₂PQ. Toon aan dat de punten R op een rechte lijn liggen, en geef een vectorvoorstelling van die lijn.

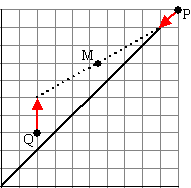
4.	Punt P beweegt vanaf t = 0 met een snelheid van 1 ^cm/_sec over de lijn y = x vanaf punt (10,10) richting de oorsprong. Punt Q beweegt vanaf t = 0 met een snelheid van 2 ^cm/_sec vanaf punt (2, 3) recht omhoog over de lijn x = 2 M is het midden van lijnstuk PQ. Beschrijf de baan van M.

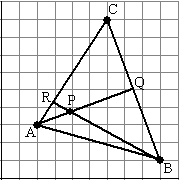
5.	Gegeven is driehoek ABC met A(2, 3) en B(9, 1) en C(6, 9) AQ is de hoogtelijn vanuit A. P is een punt op AQ zodat AP : PQ = 1 : 2. Het verlengde van BP snijdt AC in R. Bereken de coördinaten van R

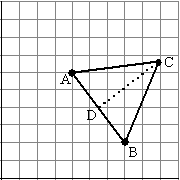
6.	ABC is een gelijkzijdige driehoek met zijden 5. A = (4, 6) en B = (7, 2)

	a.	Ga na dat inderdaad geldt dat AB = 5

	CD is de hoogtelijn vanuit C van deze driehoek.

	b.	Geef een vectorvoorstelling van CD

	Van een gelijkzijdige driehoek met zijden 5 heeft de hoogtelijn lengte 2¹/₂√3

	c.	Toon dat aan.

	d.	Bereken de coördinaten van punt C.