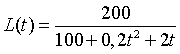De kettingregel.

© h.hofstede (h.hofstede@hogeland.nl)
Het leven is niet eerlijk!

Je hebt net allemaal regels om de afgeleide te maken geleerd en geoefend.
Dus je weet blindelings de afgeleides van √x en  4x3  en  2/x en  ....  noem maar op te geven.  Geen enkel probleem!
Maar wat gebeurt er?
Staat daar opeens geen x maar iets anders met x!!!!!

BAH!

Dus er staat bijvoorbeeld niet  √x  maar bijvoorbeeld  √(2x + 4)  of  √(x2 - 8x)  of  √(x3 + 2x + 1) of .......
in het algemeen:  √[     ]  waarbij dat blokje één of andere formule met x is.
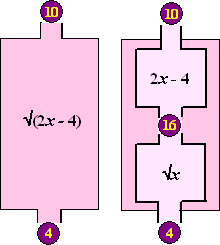
Het komt er eigenlijk op neer dat een andere functie je vóór is geweest!
Zit je net klaar om lekker op je gemak de afgeleide van √x te gaan maken, maakt een andere functie eerst  gauw van die x een [2x + 4]  of  [x2 - 8x] of  [    ] noem maar op.
Eigenlijk is de functie die je wilt differentiëren nu ineens het resultaat van twee functies na elkaar geworden.
Dat zie je hiernaast. De functie y = √(2x - 4) bestaat eigenlijk uit eerst
y = 2x - 4  en daarna  y = √x aan elkaar geschakeld.
Zo'n geschakelde functie heet daarom een KETTINGFUNCTIE.

Die laatste functie is eigenlijk degene die je wilde differentiëren (√x), maar die eerste heeft eerst x veranderd. Die is dat vervelende blokje [   ], die ervoor zorgt dat je niet f(x) moet differentiëren maar f([    ])

EN NU?? Volgende som dan maar???

Hoe het moet valt misschien met een voorbeeld te beredeneren.

Stel dat het aantal konijnen (A) in een bos in de loop van de tijd groeit volgens de formule  A(t) = 100 + 0,2t2  + 2t   (t in maanden).  Als dat bos in totaal 200 km2 groot is, dan is de leefruimte L van een konijn (dat is hoeveel een konijn gemiddeld aan ruimte heeft) afhankelijk van het aantal konijnen volgens L(A)  =  200/A .
Deze leefruimte kun je dan natuurlijk ook als functie van de tijd opschrijven:
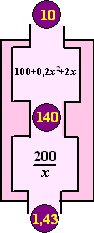
Neem t = 10. Dan is  A(10) = 140  en  L(10) ≈ 1,43.
De ketting werkt als in de figuur hiernaast en je moet L(t) eigenlijk lezen als L([  ]). Als we willen bekijken hoe snel de leefruimte afneemt als functie van de tijd, dan moeten we de afgeleide L'(t) berekenen.
 
Laten we de afgeleide gaan uitrekenen. De formule is voorlopig te moeilijk om te differentiëren, dus we vallen terug op onze grote vriend de TI-83. Voer de formule voor L(t) in bij Y1 in je grafische rekenmachine en gebruik calc - dy/dx en dan x = 10 om de helling te berekenen. Daar komt uit  L'(10) = -0,0612, en dat betekent dus dat de leefruimte per konijn na 10 maanden aan het afnemen is met 0,0612 km2  per maand.

Wat heeft dat met A(t) te maken? En met L(A)?

Laten we ook de hellingen van L(A) en A(t) berekenen bij t = 10. Misschien schiet ons iets te binnen. Je weet maar nooit.
Die hellingen kunnen we wel algebraïsch:
L(A) = 200/A = 200 • A-1  dus  L'(A) = -200 • A-2  dus  L'(140) = -0,0102.
A'(t) = 2 • 0,2t + 2  = 0,4t + 2  dus  A'(10) = 6.

Prijsvraag:  wat hebben  L'(t) = -0,0612 en  L'(A) = -0,0102  en  A'(t) = 6   met elkaar te maken?
Je hoeft geen Einstein te zijn om dat te zien, denk ik.
Het lijkt erop dat geldt:
L'(t) = L'(A) • A'(t)

Is dat logisch?
Dat kun je op twee manieren inzien. De gezond-verstand-manier  en de formule-manier.

• de gezond-verstand-manier:
Als de  leefruimte afneemt met 0,0102 km2 per konijn en tegelijkertijd neemt het aantal konijnen toe met 6 per maand, dan zal in een maand elk van die zes konijnen zorgen voor een afname in de leefruimte van 0,0102, dus in totaal zal L dan in die maand afnemen met  6 • 0,0102 = 0,0612.
• de formule-manier.
Bedenk dat geldt  y' = dy/dx
Dan geldt:

Dat leidt dan eindelijk tot de kettingregel:

Als je een differentieerregel (die je hebt geleerd voor x) wilt gebruiken,
maar in plaats van x staat er één of ander blokje (formuletje),
dan pas je die differentieerregel gewoon toe op dat blokje,
maar dan moet je daarna vermenigvuldigen met de afgeleide van dat blokje.

ofwel:

 
Voorbeelden van de regel in  werking:

Voorbeeld 1.     f(x) = √(4x - 5)
Het blokje is hier  (4x - 5)  dus de afgeleide van het blokje is 4.
De afgeleide van √x is 1/2√x  dus √[   ] geeft  1/2√[  ]
Dat geeft dus samen  f '(x) = 1/2√(4x - 5) • 4   en dat is  het zelfde als  2/√(4x - 5)

Voorbeeld 2.    f(x) = (6 - 3x)5
Het blokje is hier  (6 - 3x)   dus de afgeleide van het blokje is  -3.
De afgeleide van x5 is  5x4  dus   [  ]5  geeft  5 • [   ]4 
Dat geeft dus samen  f '(x) = 5(6 - 3x)4 • -3   en dat is het zelfde als  -15 • (6 - 3x)4

Voorbeeld 3.   f(x) =  2/(x² + x)
Het blokje is hier  (x2 + x)  dus de afgeleide van het blokje is  2x + 1
De afgeleide van  2/x  is  -2/x²   dus  2/[  ]   geeft  -2/[  ]² 
Dat geeft dus samen  f '(x) =  -2/(x² + x)² • (2x + 1)

 
  OPGAVEN
1. Geef de afgeleide van de volgende functies:
a. y = 2√(x2 + 3x)   e. y = 3(x2 + 4x - 6)3 
b. f(x) = (2x3 - x)5    f. y =  1/(4x³ - 2x) + 3x2
c. f(x) = 6/(6x + 8)²   g. f(x) = 6 - (4 - x)4 
d. y = (2x + 3) • √(2x + 3)   h. f(x) = √(1 + √x))
2. Gegeven is de functie  f(x) = (2x - x4 )3
Geef een vergelijking van de raaklijn aan de grafiek van  f  in het punt waarvoor x = 1.
     

y = -6x + 7
3. De hoeveelheid huishoudelijk afval die een stad produceert in een jaar is uiteraard afhankelijk van het aantal inwoners. Er blijkt te gelden  V(n) = 0,08√(0,1n3 + 10n)  waarin V de hoeveelheid afval (in duizenden kg) is en n het aantal inwoners (in duizenden).
a. Toon aan dat V(n) een stijgende functie is.
Als een klein stadje groeit, dan neemt de hoeveelheid afval  per inwoner  vaak eerst af. Dat komt door een efficiëntere manier van gescheiden inzamelen en verwerken van afval bij iets meer inwoners.  Wordt een stad te groot dan verdwijnt dit gunstige effect en neemt de hoeveelheid afval per inwoner juist toe. Dat komt deels doordat er meer artikelen te verkrijgen zijn en dus gekocht worden in een grotere stad, en deels doordat de sociale controle veel kleiner is. 
Voor de hoeveelheid afval per inwoner volgt uit bovenstaande formule dat die gelijk is aan 
V/n = 0,08√(0,1n + 10/n)
b. Toon dat aan.
c. Bereken algebraïsch bij welk inwoneraantal de hoeveelheid afval per inwoner minimaal is.

 10000
Een klein stadje heeft nu  (t = 0, t in jaren)  2000 inwoners, dus n = 2. Het inwoneraantal groeit echter behoorlijk, en de planologen verwachten  dat  n(t) = 2 + 0,1t2  een goede formule is om dit inwoneraantal de komende jaren te berekenen.
 
d. Bereken hoe snel de hoeveelheid afval die dit stadje produceert zal toenemen over 15 jaar.
     

551 kg/jaar
4. Examenvraagstuk HAVO wiskunde B, 1990 (deels)

Een luchtkussen is in een machine aangebracht om trillingen van een onderdeel op te vangen. Het volume van het luchtkussen verandert daarbij voortdurend. Daarmee samenhangend verandert ook de luchtdruk in het luchtkussen. Het volume (V) en de luchtdruk (P) zijn beiden functies van de tijd t. Het verband tussen luchtdruk en volume wordt gegeven door  P = 1/V
Gemakshalve worden hier voor de grootheden volume, druk en tijd niet nader gespecificeerde eenheden gebruikt.
Hieronder staat de grafiek van  V(t)  

a. Op t = 5 geldt  V = 0,5 en V ' = 0,20.  Bereken P' voor t = 5.
   

- 0,8
b. op t = 10 geldt  P = 1,25  en  P' = 0,3.  Bereken  V' voor t = 10.
     

- 0,192
       
5. Uit een lek vat stroomt olie de zee in.
Die olie vormt een cirkelvormige plas rondom het vat met een straal r en een dikte van 0,1 mm.
Op een bepaald moment is de straal van de olieplas gelijk aan 80 cm en op dat moment neemt de straal toe met 10 cm/minuut.
Hoe snel stroomt de olie op dat moment uit het vat?
     

50,26 cm3/min
       
6.
       
  Twee honden, een boxer (links) en een herder (rechts) zitten aan één touw van 20 meter lang aan elkaar vast. Het touw loopt over een katrol die op 3 meter hoogte boven hun halsbanden vastzit. Zie de tekening.
De herder wil naar rechts, de boxer wil naar links.
De herder wint, en loopt met een constante snelheid van 0,2 m/s naar rechts.
Hoe snel loopt de boxer naar achteren op het moment dat hij 4 meter van P af is?

0,98 m/s
7. De temperatuur van de lucht boven het aardoppervlak wordt op een bepaalde plaats gegeven door:
T(h) = 20 - √(10 + h2)
Daarin is h de hoogte in honderden meters en T de temperatuur in ºC.
       
  a. Op welke hoogte is de temperatuur 5ºC?
     

1466 m
  b. Hoe snel daalt de temperatuur (in ºC/m) op een hoogte van 600 meter?
     

0,00032
  Een parachutist springt op t = 0 op hoogte 2 km vanuit een vliegtuig. Hij valt naar benden, en voor zijn hoogte h geldt:  h(t) = 20 + 0,1 • (t - t2)
Daarin is h weer in honderden meters, en t in seconden.
       
  c. Bewijs met de formule dat de parachutist eerst omhoog springt en daarna past valt.
       
  d. Op welk tijdstip valt hij met 90 m/sec?
     

5 sec.
  e. Hoe snel (in ºC/sec) verandert de temperatuur voor de parachutist op t = 5?
     

-0,89
       
8.

       
  De koplampen van een auto maken twee cirkelvormige lichtplekken op een muur waar de auto naar toe rijdt met een snelheid van 3 m/s.
Met welke snelheid verandert de oppervlakte van zo'n lichtplek als de auto 6 m van de muur af is?
     

12π m2/sec
       
9. Examenvraagstuk HAVO Wiskunde B, 2002.
       
  Gegeven is de verzameling functies 
g(x) = (px + 4)3.
In de figuur hiernaast is voor een aantal waarden van p de bijbehorende grafiek getekend.

Voor elke waarde van p snijdt deze grafiek de y-as in het punt C(0,64)

De helling van de grafiek van g in het punt C is afhankelijk van de waarde van p.

Bereken exact voor welke waarde van p deze helling gelijk is aan 10.

       
10. In een kegelvormige silo (straal bovenvlak 0,5 m, hoogte 2 m) loopt een vloeistof weg met een snelheid van 1200 cm3/sec. 

De inhoud van een kegel is gelijk aan 1/3 • πr2 • h.
Als de hoogte van de vloeistof in de kegel gelijk is aan h, dan is de inhoud ervan gelijk aan  1/48πh3

       
  a. Toon deze formule aan.
       
  b. Hoe snel (in cm/sec) zakt het vloeistofoppervlak als het peil op 1 m hoogte staat?
         
11.

         
  Een auto en een trein rijden beiden richting een spoorwegovergang.  De autoweg staat loodrecht op de spoorbaan.
De auto is op t = 0  op afstand 3 km van de overgang en rijdt met 120 km/uur.
De trein is op t = 0  op afstand 2 km van de overgang en rijdt met 80 km/uur.
Oei!!
Dat gaat een botsing geven!!

Voor de onderlinge afstand A van auto en trein op tijdstip t geldt:  A(t) = √(20800t2 - 1040t + 13)
         
  a. Toon aan dat deze formule juist is.
         
  b. Geef een formule voor de relatieve snelheid v  van de auto en de trein.
         
  c. Plot de grafiek van de snelheid en leg uit wat ermee aan de hand is.
         
  d Toon aan dat je conclusies uit c)  ook al volgen uit de formule van b)
         
   
   
Erg veel vraagstukken waar je de kettingregel bij nodig hebt (en dus kunt oefenen!) kun je nog vinden in deze opgavenles over het optimaliseren van wortelfuncties.
   
 

© h.hofstede (h.hofstede@hogeland.nl)