© h.hofstede (h.hofstede@hogeland.nl)
En nu alles door elkaar.....
We hebben al erg veel verschillende principes en methodes van de kansrekening besproken.
Het wordt hoogste tijd om alles eens lekker door elkaar te gooien.
Eerst nog even de hoofdlijnen:
Principe 1:  EN  - OF
Als er twee gebeurtenissen A en B zijn, dan geldt algemeen:
P(A én B)

•

 P(A) • P(B)  met P(B) in de nieuwe situatie

•

 P(A) • P(B) als A en B onafhankelijk zijn
P(A óf B)

•

 P(A) + P(B) - P(A én B)
  Daarbij is P(A én B) nul als A en B niet tegelijk kunnen voorkomen.
 
Principe 2:  Kansboom of Vaasmodel?

Voor het berekenen van kansen hebben we twee basismethodes:

Kansboom.
• bereken de kans op een tak door de kansen te vermenigvuldigen.
• tel de gunstige takken op.

•

 speciaal geval:  binomiaal (n, p, k).
Vaasmodel.
• zonder terugleggen.
• bereken gunstig/mogelijk  met combinaties.
• maak bij voorwaardelijke kansen een kruistabel.
 
Het volgende voorbeeld laat zien hoe deze verschillende aspecten gecombineerd in een opgave kunnen voorkomen.

voorbeeld 1.

Een spin zit in zijn web en probeert de vliegen die voorbijkomen te vangen. De kans dat hij een vlieg vangt is 60%.
Maar als een spin 4 vliegen op een dag heeft gevangen, dan zit hij vol en is verder niet geïnteresseerd in vliegen.
De kans dat een voorbijkomende vlieg dan nog gevangen wordt is nul.

Op een dag komt de achtste vlieg van die dag voorbij. Hoe groot is de kans dat deze vlieg gevangen wordt?

oplossing
Je moet jezelf bedenken dat er twee verschillende mogelijkheden zijn op het moment dat de achtste vlieg de spin passeert.
Mogelijkheid A: de spin heeft al 4 vliegen gevangen van de vorige 7.
Mogelijkheid B: de spin heeft nog geen 4 vliegen gevangen van de vorige 7.

Nu geldt:  P(achtste vlieg wordt gevangen) = P(B) • 0,6.

P(B) is de kans dat de spin 3 of minder vliegen heeft gevangen van de 7 waarbij elke keer de kans op vangen 0,6 is en op niet-vangen 0,4. Dat is dus een binomiaal experiment met n = 7,  p = 0,6.
P(k ≤ 3) = binomcdf(7, 0.6, 3) = 0,289792.

De kans dat de achtste vlieg wordt gevangen is daarom  0,289792 • 0,60 = 0,1738752.
voorbeeld 2

Ik heb een trommel met 9 lollies erin:  3 kersensmaak, 3 aardbeiensmaak en 3 citroensmaak.
Op het feestje van mijn zoontje zijn 5 kinderen aanwezig, die allemaal natuurlijk een eigen lievelingssmaak hebben.
Hoe groot is de kans dat ieder zijn eigen lievelingssmaak kan krijgen?

oplossing.

Het is handiger om de kans uit te rekenen dat NIET iedereen zijn eigen lievelingssmaak kan krijgen.
Dat is zo als er 4 kinderen OF 5 kinderen zijn met dezelfde lievelingssmaak.
Zet de kinderen op volgorde en noteer hun lievelingssmaak.
5 dezelfde smaak:   kkkkk, aaaaa, ccccc en dat zijn 3 mogelijkheden.
4 dezelfde smaak:   kkkkX, aaaaX, ccccX en die X kan op vijf plekken staan en kan steeds twee mogelijke letters zijn. Dat zijn in totaal dus  3 • 5 • 2 = 30 mogelijkheden.
Het gunstige aantal mogelijkheden is daarmee 33.
Het totaal aantal mogelijkheden is  35 = 243.
De kans is dan  33/243 op NIET iedereen zijn lievelingssmaak, dus  1 - 33/243 = 210/243  op WEL iedereen zijn eigen lievelingssmaak.
voorbeeld 3

In de winter is de kans dat het regent 80%, in de rest van het jaar is die kans 40%
Het regende de afgelopen week maar liefst 5 van de 7 dagen.
Hoe groot is de kans dat het winter is?
oplossing.
Dit is een voorwaardelijke kans, want de kans op winter wordt gevraagd gegeven dat  het 5 van de 7 dagen regende.
We gaan daarom een kruistabel maken voor de eigenschappen A: het regent 5 van de 7 dagen  en  B: het is winter
In de winter is de kans op 5 van de 7 dagen regen  binompdf(7,0.8,5) = 0,2753
In de rest van het jaar is die kans binompdf(7, 0.4, 5) = 0,0774
Daarmee is de tabel hiernaast ingevuld voor 1000 dagen.
Je ziet dat de kans op winter nu  68,83/126,86 ≈ 0,54 is
  5 dagen regen niet 5 dagen regen totaal
winter 68,83 181,18 250
niet winter 58,05 691,95 750
totaal 126,86 873,13 1000
EN NU ZELF:
1. Het verjaardagsprobleem.
Hoe groot is de kans dat van een groep van 30 mensen er minstens twee op dezelfde dag jarig zijn?
     

0,7063
2. Twee spelers doen mee aan een knock-out tennis toernooi. 
Er zijn 32 deelnemers, en elke ronde wordt geloot wie tegen wie moet. Zodra een speler verliest is hij uitgeschakeld en doet niet meer mee.
Neem aan dat alle spelers even sterk zijn (dus kans 1/2 hebben om van elke andere te winnen of verliezen)

Hoe groot is de kans dat de twee spelers elkaar tegenkomen?
     

0,0625
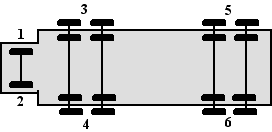
3. De onderkant van een vrachtwagen ziet eruit als hiernaast. Hij heeft 18 banden.
Er zijn 6 groepen banden. Zie de figuur.
Plotseling exploderen 4 banden. 
Hoe groot is de kans dat tenminste één van de groepen in zijn geheel kapot is?

     

0,1092
4.
Enkele vrienden spelen met elkaar het volgende kansspel:
• Iedereen betaalt als inzet €1,-
• eerste ronde: iedereen gooit met 1 dobbelsteen
• tweede ronde: wie de eerste ronde even heeft gegooid mag nog eens gooien.
• derde ronde:  wie de tweede ronde een zes heeft gegooid mag nog eens gooien.
Het spel is nu afgelopen en de pot wordt gelijkelijk verdeeld over het aantal zessen dat is gegooid. Als niemand een zes heeft gegooid blijft het geld in de pot voor de volgende ronde. 
a. Bereken de kans dat een speler meedeelt in de pot.

2/9
Voor het aantal zessen dat een speler gooit geldt bij benadering de volgende tabel;
aantal zessen 0 1 2 3
kans 0,778 0,185 0,032 0,014
b. Bereken het getal 0,185 exact.

5/27
Drie spelers spelen samen dit spel. 
c. Hoe groot is de kans dat na 8 spellen nog steeds niemand iets heeft gewonnen?
 

0,0024
d. Hoe groot is de kans dat een speler bij één spel 1/3 deel van de pot krijgt?
     

0,0157
5. Een tuinder gaat 12 bomen in een rij planten. Het zijn 3 appelbomen, 4 perenbomen en 5 kersenbomen.
Hij plant ze in willekeurige volgorde.
Hoe groot is de kans dat er nergens twee kersenbomen naast elkaar staan?
     

0,0707
6. Bij het spel Yahtzee gooi je met 5 dobbelstenen.
Een "Full House" betekent dat je van één cijfer er drie hebt gegooid en van een ander cijfer twee.

Bereken de kans op een full house.

     

0,0386
7. Examenvraagstuk HAVO Wiskunde A, 1993.
       
  Aanstekers zijn niet allemaal even goed. De ene aansteker heeft een grotere kans om een vlam te geven dan de andere. Zo'n kans noemen we de vlamkans. Neem aan dat voor iedere aansteker geldt dat de vlamkans bij iedere poging gelijk is en onafhankelijk van eerdere pogingen.
       
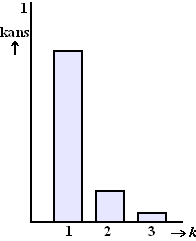
  Stel dat een aansteker een vlamkans heeft van 0,8.
In het histogram hiernaast is voor k = 1, 2 ,3 aangegeven hoe groot de kans is dat deze aansteker pas bij de k-de poging voor het eerst een vlam geeft.

     
  a. Bereken de kansen die horen bij k = 2 en k = 3
   

0,16 en 0,032
  Voordat een aansteker de fabriek verlaat wordt hij getest. Bij een test wordt de aansteker goedgekeurd als hij in maximaal 3 pogingen een vlam geeft.
Stel weer dat een aansteker een vlamkans heeft van 0,8. Deze kans is vrij hoog, maar dat betekent nog niet automatisch dat de aansteker wordt goedgekeurd.
     
  b. Bereken de kans dat die aansteker goedgekeurd wordt.
   

 0,992
 
  c. Bij welke vlamkans is de kans dat een aansteker goedgekeurd wordt gelijk aan  95%?
     

0,368
  Andere manieren van testen zijn ook mogelijk. Bijvoorbeeld:  elke aansteker wordt 10 keer achter elkaar geprobeerd. Als hij drie of meer keren achter elkaar heeft geweigerd in die serie van 10 wordt de aansteker afgekeurd, anders goedgekeurd.

Bij een bepaalde aansteker krijgt men het volgende resultaat bij de test:

N N J N N J N N J N    (N = werkt niet, J = werkt wel)

Deze aansteker wordt dus goedgekeurd.
       
  d. Hoeveel verschillende series van 3 keer J en 7 keer N zijn er mogelijk waarbij de aansteker goedgekeurd wordt?
       
  e. Hoe groot is de kans dat een aansteker met vlamkans 0,8 goedgekeurd wordt?
       
8. Een kubus van 3 bij 3 bij 3 wordt helemaal rood geverfd.
Vervolgens wordt hij in 27 gelijke kubusjes van 1 bij 1 bij 1 gesneden.
Die 27 kubusjes doe je in een doos, en daar pak je willekeurig een kubusje uit.
Dat gooi je op tafel.

     
  a. Hoe groot is de kans dat het vlak van dat kubusje dat bovenop ligt rood is?
     
  b. Hoe groot is die kans als je een n bij n bij n kubus verdeelt in allemaal kubusjes van 1 bij 1 bij 1?
       
       
9. Anton, Betty, Conny, Diana en Erik gaan op willekeurige plaatsen om een ronde tafel zitten.

Hoe groot is de kans dat dat Bettie precies tussen Anton en Conny in komt te zitten (dus dat Bettie naast Anton én naast Conny zit)?

     

1/6
       
10. Een  jongetje gaat langs de deuren om kinderpostzegels te verkopen. Hij verkoopt mapjes van 1 euro.  Het ventje heeft echter geen wisselgeld bij zich, en moet dus maar hopen dat de mensen vaak gepast kunnen betalen. Pas als hij een aantal mapjes van 1 euro heeft verkocht, dan heeft hij natuurlijk wel wisselgeld. Neem aan dat alle mensen óf gepast betalen, óf met een muntstuk van 2 euro (waarbij ze dus een euro terug moeten krijgen). De kans op beide mogelijkheden is 0,5.
       
  a. Hoe groot is de kans dat hij de eerste drie mapjes die hij verkoopt zonder wisselproblemen kan verkopen?
     

3/8
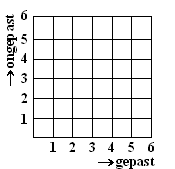
  b. Geef in het rooster hiernaast alle routes aan waarbij er bij de eerste zes mapjes niemand op wisselgeld hoeft te wachten.

Hoe groot is de kans dat er bij de eerste zes mapjes geen wisselproblemen zijn?

   

20/64
  c. Hoe groot wordt de kans op vraag b) als het jongetje in het begin twee losse euromunten bij zich heeft?
   

50/64
 
       
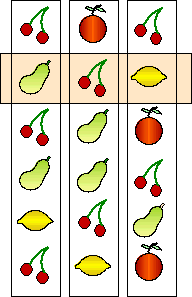
11. Een fruitautomaat bestaat uit drie onafhankelijk van elkaar draaiende schijven met daarop fruitsymbolen getekend. We bekijken in deze opgave een klein fruitautomaatje met kers, peer, citroen en tomaat. Op elke schijf staan zes van deze symbolen. In de figuur hiernaast zie je hoe de symbolen over de schijven zijn verdeeld. Op de eerste schijf staat bijvoorbeeld 3 keer kers, 2 keer peer en 1 keer citroen.
Door de schijven te laten draaien en dan te stoppen komen er drie willekeurige symbolen voor het venster te staan, van elke schijf één. In de figuur zie je voor het venster peer - kers - citroen staan. 

     
  a. Bereken de kans dat bij drie keer draaien de eerste schijf steeds peer geeft.
   

1/27
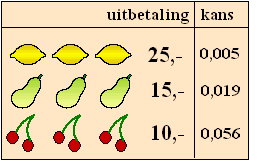
  Er zijn drie manieren om geld te winnen. De uitbetaling staat in de tabel hiernaast (de bedragen zijn in euro's). De kans op elke uitbetaling staat ook aangegeven.

     
  b. Bereken de drie kansen uit de tabel exact.
   

1/216, 4/216, 12/216
  c. Bereken de kans dat iemand die twee keer speelt in totaal 25 euro krijgt.
   

0,007
 
  d. Hoeveel verwacht je gemiddeld per keer spelen te krijgen?
     

0,949
       
12. Het is het jaar 2016 en Nederland heeft de finale van het wereldkampioenschap voetbal gehaald. In deze finale tegen Italië is het 0-0 geworden en ook na verlenging is het nog steeds 0-0. Kortom: er worden strafschoppen genomen.
Nadat elk team 10 strafschoppen heeft genomen is de stand nog steeds gelijk.

We gaan nu "Sudden Death" spelen. Dat betekent dat steeds na 2 strafschoppen (één van elk team) er gekeken wordt of er al een winnaar is. Als dat zo is, is het afgelopen,  anders komen de volgende twee strafschoppen.
  De kans dat een speler van Nederland scoort is 63%, voor Italië is dat 82%
       
  Voor zo'n serie van twee strafschoppen blijkt de volgende tabel te gelden:
       
 
Gebeurtenis Kans
Italië wint 0,30
Nederland wint 0,11
Geen beslissing 0,58
       
  a. Bereken deze kansen in vier decimalen nauwkeurig
     

0..034, 0.1134, 0.5832

  b. Bereken de kans dat Italië na drie series of minder van Nederland wint.
     

0,5835
  c. Bereken in drie decimalen nauwkeurig de kans dat Nederland uiteindelijk wint.
     

0,272
       
13. Een vaas bevat evenveel rode als blauwe knikkers (minstens 4 in totaal).
Je haalt er 4 uit en berekent de kans op 2 roden.
Dat kun je doen zonder terugleggen, maar ook met terugleggen, en dat geeft twee verschillende kansen.
Als je het aantal knikkers laat toenemen, dan worden deze twee kansen langzaam aan elkaar gelijk. Voor welk totaal aantal knikkers in de vaas is het verschil tussen deze beide kansen voor het eerst minder dan 1%?
     

78
     
14. Een kaartspel bestaat uit 16 plaatjes (AHVB van elke soort) en 36 niet-plaatjes (T98765432 van elke soort).
Een volledig kaartspel wordt geschud zodat alle kaarten willekeurig door elkaar zitten.
Hoe groot is de kans dat in de stapel kaarten die je dan hebt er nergens 2 plaatjes naast elkaar zitten?
       
 
hint:   leg de niet-plaatjes op een rij, op hoeveel manieren kunnen de plaatjes daartussen?
     

0,000124
       
15. Een kameleon heeft een lange kleverige roltong waarmee hij voorbijvliegende vliegen kan vangen. Mannetjeskameleons zijn daarin beter dan vrouwtjes. Als er een vlieg voorbijkomt, is de kans 80% dat een mannetjeskameleon hem vangt, en bij een vrouwtje is dat slechts 65%. Gelukkig voor de vliegen is slechts 30% van de kameleons een mannetje
 
 
     
  a. Als een vlieg langs een kameleon vliegt, en niet wordt gevangen, hoe groot is dan de kans dat de kameleon een mannetje is?
     

0,1967
 

Als een kameleon op een dag al 10 vliegen heeft gevangen, dan wordt hij lui, en dan is de kans dat hij een volgende vlieg vangt voor mannetjes en vrouwtjes nog maar 40%

Op een dag komt de 11de vlieg voorbijgevlogen langs een mannetjeskameleon
       
  b. Hoe groot is de kans dat de kameleon die vlieg zal vangen?
     

0,7570
16. examenvraagstuk VWO, 1982
       
  In een vaas V bevinden zich twee rode, drie gele en vijf blauwe knikkers.
       
  a, Men neemt aselect een greep van drie knikkers uit V.
Bewijs dat de kans dat in deze greep alle drie de kleuren voorkomen gelijk is aan 1/4.
Bereken de kans dat in deze greep precies één kleur niet voorkomt.
       
  b. Men neemt aselect en met terugleggen vijftig maal een greep van drie knikkers uit V.
Bereken in vier decimalen nauwkeurig de kans dat daarbij ten hoogste dertig grepen zijn waarin niet alle kleuren rood, geel en blauw voorkomen.
       
  c. Men trekt aselect en zonder terugleggen telkens één knikker uit V totdat men voor de tweede maal een rode knikker heeft verkregen. Het aantal trekkingen is een stochast R
Stel de kansverdeling van R op.
       
17. examenvraagstuk VWO, 1983
       
  Een vaas bevat twee gele, drie rode en vijf blauwe knikkers.
       
  a. Men trekt aselect in één greep drie knikkers uit de vaas en legt ze terug in de vaas.
Dit experiment voert men tien maal uit.
Bereken in vier decimalen nauwkeurig de kans dat er bij deze tien grepen precies vier grepen zijn waarin geen blauwe knikker voorkomt.
       
  b. Men trekt aselect in één greep vier knikkers uit de vaas.
Bereken de kans dat er evenveel gele als rode knikkers in de vaas achterblijven.
       
  c. Men trekt aselect en met terugleggen tien maal een knikker uit de vaas.
Bereken in vier decimalen nauwkeurig de kans dat er bij deze tien trekkingen precies drie maal een gele en precies drie maal een rode knikker getrokken wordt.
       
18. examenvraagstuk VWO, 1984
       
  Een vaas bevat n balletjes, genummerd van 1 tot en met n  (n ≥ 3)
Een aselecte greep van drie balletjes uit de vaas is een trekking.
Na een trekking worden de nummers van de getrokken balletjes genoteerd; daarna worden de getrokken balletjes teruggelegd in de vaas.
       
  a. Neem n = 12.
Bereken de kans dat in een trekking de som van de nummers kleiner is dan 11.
       
  b. Voor welke n geldt: de kans dat een trekking drie balletjes met drie opeenvolgende nummers oplevert is 1/100?
       
  c. Neem n = 6
Bereken in drie decimalen nauwkeurig de kans dat in vijf trekkingen het balletje met nummer 1 precies drie maal voorkomt en het balletje met nummer zes niet voorkomt.
       
19. examenvraagstuk VWO, 1999.

In de Verenigde Staten zijn loterijen erg populair. Een ervan is Powerball. Voor 1 dollar kun je meedoen. Je moet dan een formulier invullen waarop een witte en een rode tabel staan, elk met de getallen 1 tot en met 45. In de witte tabel moet je vijf getallen omcirkelen, en in de rode tabel één getal. Bij de trekking worden aselect zonder teruglegging vijf ballen getrokken uit een trommel met 45 genummerde witte ballen en één bal uit een andere trommel met 45 genummerde rode ballen. De organisatie publiceert het volgende overzicht:
       
 
goed geraden prijs kans
5 witte en de rode
5 witte, niet de rode
4 witte en de rode
4 witte, niet de rode
3 witte en de rode
3 witte, niet de rode
2 witte en de rode
1 witte en de rode
0 witte en de rode		 jackpot
$ 100000
$ 5000
$100
$100
$5
$5
$2
$1		 1 op 54979155
1 op 1249526
1 op 274896
1 op 6248
1 op 7049
1 op 160
1 op 556
1 op 120
1 op 84
       
  Alle prijzen behalve de jackpot zijn vaste bedragen per deelnameformulier. De getallen in de kolom 'kans' zijn afgerond op gehele getallen.
Volgens het overzicht is de kans op $5000 gelijk aan  1/274896
       
  a. Toon met een berekening aan dat de kans op $5000 klopt.
       
  De klantenservice van de organisatie wordt regelmatig benaderd door mensen die menen dat de kans op $1 niet 1 op 84 maar 1 op 45 is. De klantenservice legt uit dat zij zich vergissen in wat je goed geraden moet hebben om de prijs van $1 te winnen.
       
  b. Bij welke voorwaarde zou de kans op een prijs wel 1 op 45 zijn? Licht je antwoord toe.
       
  De organisatie stort van elke ingezette dollar 0,3082 dollar in de jackpot. De jackpot wordt na elke trekking verdeeld over alle deelnameformulieren waarop alles goed geraden is. Als die er niet zijn, wordt het bedrag uit de jackpot toegevoegd aan de jackpot van de volgende trekking.
In 1998 viel de jackpot pas na zestien trekkingen op precies één deelnameformulier.
De winnaar kreeg een bedrag van 190 miljoen dollar.
       
  c. Hoeveel deelnameformulieren waren er in totaal ingevuld bij deze zestien trekkingen? Licht je antwoord toe.
       
  De organisatie gaat er van uit dat per trekking 19,72% van het ingezette geld besteed moet worden aan de uitbetaling van de prijzen behalve de jackpot.
       
  d. Toon met een berekening aan dat die 19,72% naar verwachting klopt.
       
  Er zijn twee trekkingen per week. Iemand speelt een jaar lang (104 trekkingen) bij elke trekking met één formulier mee.
       
  e. Bereken de kans dat hij hierbij meer dan één keer een prijs wint.
       
20. Examenvraagstuk HAVO Wiskunde B, 2001

Een restaurant van een warenhuis bestelt een grote partij perssinaasappels voor de bereiding van verse jus d'orange. De sinaasappels worden aangevoerd in volle dozen van 50 stuks.

De ervaring leert dat ongeveer één van de honderd sinaasappels beschimmeld is. Ga er bij de vragen 1, 2  en 3 van uit dat de kans op een beschimmelde sinaasappel 0,01 is.

Voor een groot glas jus d'orange zijn drie sinaasappels nodig. Een medewerker pakt aselect drie sinaasappels.
       
  a. Bereken de kans dat er precies één beschimmelde sinaasappel bij zit. Geef je antwoord in drie decimalen nauwkeurig.
     

0,029
  De kans op een doos sinaasappels zonder schimmel is ongeveer gelijk aan 0,605.
       
  b. Laat met een berekening zien dat dit zo is.
       
  Bij een kwaliteitscontrole worden vijf volle dozen sinaasappels gecontroleerd. Een doos is "in orde" als er geen enkele beschimmelde sinaasappel in zit. Als vier of vijf van de dozen niet in orde zijn wordt de partij afgekeurd.
       
  c. Bereken de kans dat de partij wordt afgekeurd. Geef je antwoord in drie decimalen nauwkeurig.
     

0,083
       
21. Examenvraagstuk HAVO Wiskunde B, 2003

Bij de introductie van een nieuw biermerk organiseert de fabrikant een reclameactie. Op de binnenkant van elke kroonkurk laat hij een letter van het alfabet afdrukken. Alle 26 letters van het alfabet worden in gelijke hoeveelheden afgedrukt. De bierflesjes worden willekeurig over de bierkratten verdeeld.
Wie een kroonkurk met de letter P inlevert krijgt een gratis flesje bier van dit merk.
Een klant drinkt elke dag één flesje bier van het nieuwe merk.
       
  a. Bereken hoeveel flesjes bier hij moet drinken om tien gratis flesjes te kunnen verwachten.
     

260
  b. Bereken de kans dat hij op de derde dag voor het eerst een kroonkurk met de letter P heeft. Rond je antwoord af op drie decimalen.
     

0,036
  c. Bereken de kans dat hij bij de eerste tien flesjes minstens één letter P heeft. Rond je antwoord af op drie decimalen.
     

0,324
  d. Bereken de kans dat hij met de letters van de eerste vier kroonkurken het woord 'PILS'  kan vormen. Geef je antwoord in procenten. Rond af op vier decimalen.
     

0,0053%
       
22. Examenvraagstuk HAVO, Wiskunde B, 2007.

Het spel ‘Biggen’ wordt gespeeld met twee ‘dobbelstenen’ in de vorm van kleine plastic varkentjes. De spelers werpen met deze dobbelstenen, biggen genaamd. Hoeveel punten een speler krijgt, hangt af van hoe deze biggen terecht komen. Doel van het spel is zo veel mogelijk punten te scoren. Wie het eerst 100 punten of meer heeft, wint.

Een big kan op zes verschillende manieren terecht komen: op zijn linkerzij, op zijn rechterzij, rechtop op zijn poten, op zijn rug, op zijn snuit of op zijn wang. (Zie de foto’s.) De big is niet volledig symmetrisch. Zo is de kans dat de big op zijn linkerzij terecht komt niet gelijk aan de kans dat hij op zijn rechterzij terecht komt. Bovendien kan de big niet op zijn rechterwang blijven liggen, maar wel op zijn linkerwang. Daarom duiden we deze situatie simpelweg aan met wang.
       
 
       
  In de volgende tabel zijn de kansen voor de verschillende worpen met één big en de punten die daarbij horen gegeven.
       
 
big valt op linkerzij rechterzij poten rug snuit wang
kans 0,29 0,35 0,08 0,23 0,04 0,01
punten 0 0 5 5 10 15
       
  Uit deze tabel blijkt dat bij 50 worpen met één big de big naar verwachting vier keer (50×0,08) op zijn poten terecht komt. In de praktijk is het natuurlijk wel mogelijk dat de big acht keer of vaker op zijn poten terecht komt.
       
  a. Bereken de kans dat een big bij 50 worpen acht keer of vaker op zijn poten terecht komt.
     

0,04379
  Bij een worp met twee biggen worden de punten van de twee biggen opgeteld. Dit geldt echter niet wanneer bij een worp beide biggen op exact dezelfde manier terecht zijn gekomen. Dan krijg je namelijk meer punten. Zie onderstaande tabel.
       
 
beide biggen
vallen op		 linkerzij rechterzij poten rug snuit wang
punten 1 1 20 20 40 60
       
  Zolang een speler doorgaat met gooien, worden de punten van zijn worpen bij elkaar opgeteld. Als hij vrijwillig stopt, worden zijn punten genoteerd en is de volgende speler aan de beurt.
Het doorgaan met gooien heeft echter ook een risico: als bij een worp één big op zijn linkerzij valt én de andere big op zijn rechterzij, moet de speler stoppen en is hij alle punten van deze beurt kwijt. De kans dat dit gebeurt, is afgerond op 2 decimalen 0,20.
       
  b. Toon dit met een berekening aan.
       
  c. Bereken de kans dat een speler drie keer achter elkaar kan gooien zonder dat hij zijn punten kwijt raakt.
     

0,5
  Twee spelers spelen het spel. Op een gegeven moment heeft een van de spelers 98 punten. Hij is aan de beurt. Hij wil graag weten hoe groot de kans is dat hij het spel zal winnen in deze beurt. Je mag er daarbij van uitgaan dat zodra de speler 100 punten of meer heeft gehaald, hij zal stoppen met gooien omdat hij dan al heeft gewonnen. Je mag er ook van uitgaan dat wanneer de speler in zijn eerste worp 1 punt haalt, hij zal doorgaan met gooien.
       
  d. Bereken de kans dat deze speler in deze beurt het spel wint.
     

0,7587
       
23. Examenvraagstuk VWO, Wiskunde B, 2006.

Een spelprogramma op televisie telt bij aanvang 16 deelnemers. Het spel wordt gespeeld in vier rondes. In elke ronde nemen de spelers het in een spelletje van één-tegen-één tegen elkaar op. Van elk tweetal gaat de winnaar door naar de volgende ronde; de verliezer doet niet meer mee. In elke ronde wordt het aantal deelnemers dus gehalveerd; men spreekt van een knock-out-systeem.
De spelletjes zijn van zodanige aard dat de uitslag volledig bepaald wordt door het toeval. Bij elk spelletje hebben beide spelers dus kans 1/2 om te winnen.
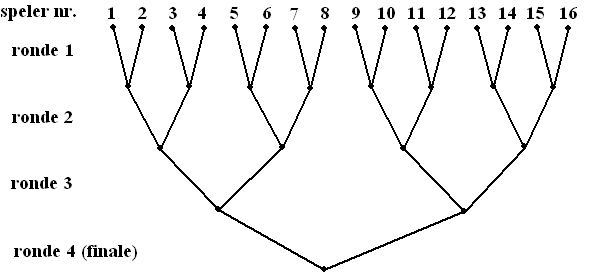
Vooraf wordt een speelschema opgesteld; zie de volgende figuur.
       
 

       
  Elke deelnemer krijgt door loting een nummer. Dit nummer is zijn plaats in het schema. Boven in het schema zie je wie tegen wie speelt in de eerste ronde. Na de eerste ronde zijn er nog acht spelers over. De winnaar van de spelers 1 en 2 speelt in de tweede ronde tegen de winnaar van de spelers 3 en 4, enzovoort. In de vierde ronde wordt de finale gespeeld door de twee overgebleven deelnemers.

Er nemen 8 mannen en 8 vrouwen aan het spelprogramma deel.
       
  a. Bereken de kans dat de nummers 1 tot en met 4 worden gegeven aan drie mannen en een vrouw.
     

16/65
  b. Bereken de kans dat speler 1 de finale speelt tegen speler 16 en speler 1 deze finale wint.
     

1/128
  c. Elke deelnemer speelt 1, 2, 3 of 4 rondes.
Bereken de verwachtingswaarde van het aantal rondes dat een deelnemer speelt.
     

1,875
  In een jaar is het spelprogramma 52 keer op televisie geweest. Elke keer hebben er evenveel mannen als vrouwen meegedaan. Er is enige twijfel of elke deelnemer wel evenveel kans heeft om het spelprogramma te winnen. Misschien hebben vrouwen meer kans.
Daarom wordt het aantal keren geteld dat een vrouw het spelprogramma won. Daarna berekent men de kans op dat aantal of een hoger aantal, aangenomen dat alle deelnemers evenveel kans hebben om het spelprogramma te winnen. Het aantal wordt abnormaal hoog gevonden als deze kans kleiner is dan 5%.
       
  d. Bereken welke aantallen vrouwelijke winnaars abnormaal hoog worden gevonden.
     

33 of meer
       
24. Examenvraagstuk VWO, Wiskunde B, 2007.

Een toets bestaat uit tien meerkeuzevragen. Elke vraag heeft drie alternatieven, waarvan er precies één het juiste antwoord op de vraag geeft. Elke leerling maakt een lijstje met antwoorden. Bij het nakijken wordt er een controle op spieken uitgevoerd. We werken in deze opgave met het volgende model voor leerlingen die goed voorbereid meedoen aan de toets:
  -
-
-		 de kans dat ze bij een vraag het juiste antwoord kiezen is 0,8
de kans dat ze bij een vraag het ene onjuiste alternatief kiezen is 0,1
de kans dat ze bij een vraag het andere onjuiste alternatief kiezen is ook 0,1
       
  a. Een leerling die goed geleerd heeft, en dus aan bovenstaand model voldoet, maakt de toets. Bereken de kans dat ten minste één van de tien vragen door hem fout wordt beantwoord.
     

0,8926
  Twee leerlingen die beiden goed geleerd hebben, en dus aan bovenstaand model voldoen, maken de toets. De kans dat zij bij een willekeurige vraag hetzelfde antwoord geven is 0,66.
       
  b. Toon dit aan.  
       
  De twee leerlingen blijken precies hetzelfde antwoordenlijstje ingeleverd te hebben. Ze hebben dus allebei dezelfde vragen goed beantwoord en bij de fout beantwoorde vragen hebben ze hetzelfde foute alternatief gekozen. De docent vraagt zich af of er gespiekt is. Hij berekent de kans dat twee leerlingen die zich beiden goed op de toets hebben voorbereid en die niet gespiekt hebben, toch precies dezelfde antwoordenlijstjes inleveren. Als deze kans kleiner is dan 1%, zal de docent concluderen dat er gespiekt is en een strafmaatregel treffen. Als deze kans 1% of groter is, zal hij geen strafmaatregel treffen.
       
  c. Zal de docent een strafmaatregel treffen? Licht je antwoord toe.
     

NEE: 0,0157
       
25. In de M&M fabriek worden blauwe, oranje, gele, rode en groene M&M’s gemaakt. Van alle gemaakte M&M’s is  30% blauw, 20% oranje, 20% geel, 15% rood en 15% groen.
Om een zakje M&M’s te vullen worden willekeurig uit deze enorme voorraad  50 M&M’s gekozen om een zakje te vullen. Daardoor kan het aantal M&M’s van een kleur per zakje variëren.

       
  a. Leg uit waarom je dit probleem mag opvatten als een trekking met terugleggen.
       
  b.

Hoe groot is de kans dat er in dit zakje precies 10 oranje M&M’s zitten?
     

 0,1398
  Stel dat in het zakje uiteindelijk van elke kleur 10 stuks zitten

     
  c. Als je er dan willekeurig 5 M&M’s uithaalt, hoe groot is dan de kans op precies 2 blauwen?
     

0,2098
26. Examenvraagstuk VWO, Wiskunde C, 2013.
       
  Kakkerlakkensalade is een kaartspel uit Duitsland. Een variant van het spel wordt gespeeld met 112 groentekaarten met daarop de groenten paprika, bloemkool, sla en tomaat. Van elk van deze vier soorten groente zijn er evenveel kaarten. Aan het begin van het spel worden de kaarten geschud en krijgen alle spelers evenveel kaarten.

Annet, Beyza, Carin en Dick spelen dit spel.

Dick schudt de kaarten en geeft als eerste Annet vier kaarten uit het volledige spel kaarten.
       
  a. Bereken de kans dat Annet bij haar eerste vier kaarten precies twee bloemkoolkaarten krijgt.
     

0,2122
  Tijdens een vakantie gaan deze vier vrienden het spel 150 keer spelen.
Annet is benieuwd hoe vaak de eerste kaart die uit een volledig spel gedeeld wordt een tomaatkaart zal zijn.
       
  b. Bereken de kans dat dit vaker dan 37 keer gebeurt.  
     

0,4937
       
27. De wiskunde kermis....
Op een kermis staat een kraampje waar je door te gokken geld kunt winnen en verliezen.
  Men wacht steeds tot er vier deelnemers zijn. Die betalen elk €1,-  en krijgen elk een dobbelsteen.
 
Wie bij de eerste worp 6 gooit mag straks meedelen in de prijs, en gooit verder niet meer.
Wie bij de eerste worp 1 of 2 gooit is af, en gooit verder niet meer.
Wie bij de eerste worp 3, 4, 5 gooit mag nog een keer gooien.

Bij de tweede worp geldt precies hetzelfde als bij de eerste worp.

Bij de derde worp  krijg mag iedereen die 6 gooit meedelen in de prijs, de rest is af.

Alle spelers die mee mogen delen in de prijs verdelen daarna eerlijk onder elkaar het ingelegde geld.

De kans dat iemand meedeelt in de prijs is  7/24
       
  a. Toon dat aan.
       
  b. Bereken de kans dat jij als enige het gehele inleggeld wint.
     

0,1037
  c. Bereken hoeveel geld de eigenaar van dit spel aan wie je het inleggeld moet betalen gemiddeld per spel zal winnen.
     

1,01
  d. Bereken hoeveel worpen iemand gemiddeld doet.
     

1,75
       
28. Een fabrikant van serviezen produceert borden, die op grond van eventuele kleine productiefoutjes in drie kwaliteitsklassen A, B en C worden ingedeeld.
De volgende tabel geeft de aantallen van de verschillende soorten borden en de bijbehorende prijs van een bord.
       
 
klasse A B C
aantal 50% 30% 20%
prijs €4,- €2,- €1,-
       
  a. Bereken de kans dat drie willekeurig gekozen borden tot drie verschillende klassen behoren.
     

0,18
  b. Bereken de kans dat drie willekeurig gekozen borden samen minder dan €10,- zullen kosten
     

0,65
  c. Hoeveel zul je gemiddeld voor een willekeurig gekozen bord moeten betalen?
     

€2,80
  d. Hoe groot is de kans dat een partij van 100 borden minstens 25 borden van klasse C zal hebben?
     

0,1314
29. Voor mij liggen 6 portemonnees met in elk 4 briefjes van €20  en  12 briefjes van  €10.
Ik ga willekeurig 6 briefjes pakken en wil graag precies €80 hebben.
Die briefjes kan ik op twee verschillende manieren pakken:
       
  1. Uit elke portemonnee 1 briefje
  2. Uit één portemonnee 6 briefjes.
       
  De kans dat ik bij methode 1 precies €80 heb is groter dan bij methode 2.
       
  a. Hoeveel groter?  
     

0,4597
  Oh, wacht; er is nog een derde methode:  Kies willekeurig drie portemonnees uit en neem uit elke 2 briefjes.
       
  b. Hoe groot is nu de kans op precies €80?  
     

0,3094
       
30. Examenvraagstuk VWO Wiskunde C, 2017-II
       
 

Aan het eind van de achttiende eeuw kon je in het casino van de Russische stad Sint-Petersburg een bijzonder spel spelen. Hiervoor moest de speler eerst een vast aantal roebels  inzetten. Deze inzet laten we in deze opgave buiten beschouwing. Het spel ging als volgt:
Het casino legt 1 roebel in de pot. Vervolgens mag de speler net zo lang gooien met een zuiver muntstuk, tot hij munt gooit. Dan is het spel ten einde en ontvangt de speler de inhoud van de pot. Elk keer als de speler kop gooit, verdubbelt de bank de inhoud van de pot en mag de speler opnieuw het muntstuk gooien.
De speler ontvangt dus 1 roebel als hij met de eerste worp al munt gooit.
Als hij bijvoorbeeld eerst drie maal kop (k) gooit en dan munt (m), ontvangt hij 8 roebel.
De kans hierop is P(kkkm) = (1/2 • 1/2 • 1/2 ) • 1/2 = (1/2)4 =  1/16

De kans dat de speler in een spel 8 roebel of meer ontvangt is 1/8
       
  a. Toon dit aan.
       
  Een speler speelt het spel vier keer.
       
  b. Bereken de kans dat hij minstens één keer 8 roebel of meer ontvangt.
     

0,4138
  Na vier keer spelen van het spel heeft een speler twee keer 1 roebel, één keer 2 roebel en één keer 8 roebel ontvangen.
       
  c. Bereken de kans dat dit zich voordoet.
     

0,046875
  Het bedrag dat een speler kan ontvangen, loopt snel op. Maar de kans om zo’n hoog bedrag te ontvangen, wordt ook snel heel klein.
       
  d. Bereken de kans dat een speler in één spel meer dan 5000 roebel ontvangt.
     

0,000122
  In dit spel is het mogelijk dat de speler een heel groot bedrag ontvangt. De kans hierop is echter heel klein.
Het casino wil niet te veel risico lopen en daarom wordt een extra regel ingevoerd. De speler mag in een spel maximaal vijf keer met het muntstuk gooien. Als hij dan nog geen munt heeft gegooid, krijgt hij dus niets uitbetaald.
       
  e. Bereken de verwachte uitbetaling aan deze speler.
     

2,5 roebel
       
 

© h.hofstede (h.hofstede@hogeland.nl)