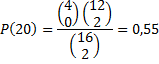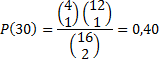© h.hofstede (h.hofstede@hogeland.nl)

       
1. P(minstens 2 op dezelfde dag = 1 - P(allemaal op een verschillende dag)
P(allemaal verschillend) = 1 • 364/365 • 363/365 • ... • 336/365 = 0,2937
P(minstens 2 op dezelfde dag) = 1 - 0,2937 = 0,7063
       
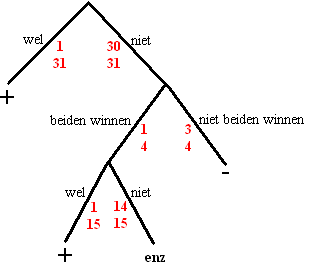
2. Zie het begin van de kansboom hiernaast

P(elkaar tegenkomen) = P(1e ronde) + P(niet in eerste, beiden winnen, wel in 2e) + .....

=  1/31    (in eerste ronde)
+ 30/31 • 1/4 • 1/15   (in tweede ronde)
+ 30/31 • 1/4 • 14/15 • 1/4 • 1/7  (in derde ronde)
+ 30/31 • 1/4 • 14/15 • 1/4 • 6/7 •  1/4 •  1/3  (in vierde ronde)
+ 30/31 • 1/4 • 14/15 • 1/4 • 6/7 • 1/4 •  2/3 • 1/4 • 1 (in finale)
= 0,03226 + 0,01613 + 0,00806 + 0,00403 + 0,00202
Daar komt 0,0625 uit.

Het kan ook zo:
  De kans is voor iedereen gelijk: het probleem is symmetrisch.
Er worden 16 + 8 + 4 + 2 + 1 = 31 wedstrijden gespeeld met 2 spelers, dus 62 keer wordt er door een speler gespeeld.
Dat is gemiddeld 62/32 wedstrijden per speler.
De kans om de ander te treffen is elke keer 1/31 dus samen geeft dat  62/32 • 1/31 = 0,0625
       
3.

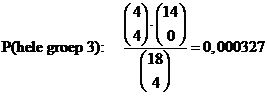  En die kans is voor de andere groepen ook 0,000327
 		  
 

 
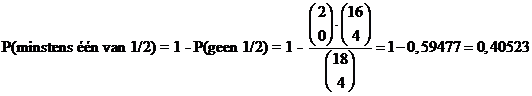
  Omdat de gebeurtenissen elkaar uitsluiten mag je de kansen optellen.
Samen geeft dat kans  4 • 0,000327 + 0,40523 = 0,4065
       
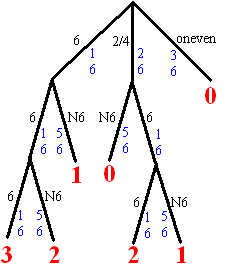
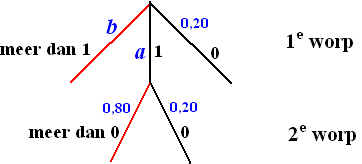
4. a. Zie de kansboom hiernaast. Rood staat het aantal gegooide zessen, blauw staan de kansen

P(0 zessen) = 3/6 + 2/6 • 5/6 = 7/9
P(meedelen) = 1 - 7/9 = 2/9
 

     
  b. P(1 zes) = 1/6 • 5/6 + 2/6 • 1/6 • 5/6 = 5/27
     
  c. P(speler heeft nul zessen) = 0,778
P(3 spelers hebben 8 spellen lang 0 zessen)
= P(24 keer nul zessen) = 0,77824 = 0,0024
       
  d. Je krijgt 1/3 van de pot als je 1/3 van het aantal zessen hebt gegooid.
Dat is  (1 van de 3) of (2 van de 6) of (3 van de 9)
Laten we de kans uitrekenen dat de eerste speler 1/3 van de pot krijgt:

= P(111) + P(120) + P(102) + P(222) + P(231) + P(213) + P(333)
= 0,1853 + (0,185 • 0,032 • 0,778) • 2 + 0,0323 +  (0,032 • 0,185 • 0,014) • 2 + 0,0143
= 0,0157
       
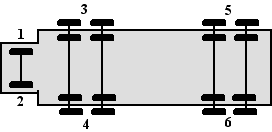
5. Het totaal aantal manieren om deze bomen te planten  is het aantal rijtjes AAAPPPPKKKKK
Dat zijn er (12 nCr 3) • (9 nCr 4) = 27720

Hoeveel rijtjes zijn er zonder twee kersenbomen naast elkaar?
plant eerst de appel- en perenbomen:  AAAPPPP kan op  7 nCr 3 = 35 manieren.
In het rijtje  •A•A•A•P•P•P•P•  staan 8 stippen waarvan je er 5 moet kiezen om een kersenboom te planten.
Dat kan op  8 nCr 5 = 56 manieren.
In totaal zijn er dus 35 • 56 = 1960 manieren om de bomen te planten zonder twee kersenbomen naast elkaar..

De kans is dan  1960/27720 = 0,0707
       
6. De kans op ιιn specifiek fullhouse, bijv.  66655  is  (1/6)5 • (5 nCr 3) = 0,001286
Hoeveel verschillende full-housen zijn er?
Voor het drietal zijn er  6 mogelijkheden, en daarna voor het tweetal nog 5, dus 6 • 5 = 30
De kans is dan 30 • 0,001286 = 0,0386
       
7. a. P(k = 2) = P(NW) = 0,2 • 0,8 = 0,16
P(k = 3) = P(NNW) = 0,2 • 0,2 • 0,8 = 0,032
       
  b. P(geen vlam in 3 pogingen) = 0,2 • 0,2 • 0,2 = 0,008
P(minstens ιιn vlam) = 1 - 0,008 = 0,992
       
  c. P(afkeuren) = 0,05 dus  p3 = 0,05
Dan is p = 0,051/3 = 0,3684
       
  d. (10 nCr 3) = 120  
       
  e. P(goedkeuren) = P(0 weigeringen OF 1 weigering OF 2 weigeringen)
Het aantal weigeringen is binomiaal verdeeld
n = 10
p = 0,2
P(X ≤ 20 binomcdf(10, 0.2, 2) = 0,6778
       
8. a. Er zijn 3 • 3 • 3 = 27 kubusjes, dus 27 • 6 = 162 zijvlakken
Daarvan zijn er 9 • 6 = 54 rood
Omdat elk vlakje even grote kans heeft bovenop te komen is de kans  54/162 = 1/3
       
  b. dan zijn er n3 kubusjes, dus 6n3 zijvlakken.
Daarvan zijn er  6n2 rood
De kans is dus 6n³/6n² = 1/n
       
9. Bereken de kans dat dat gebeurt met Bettie op de noordelijkste plaats.
Dan zijn er voor Anton en Connie twee mogelijkheden
Voor Diana en Erik ook 2 mogelijkheden, dus er zijn 2 • 2 = 4 gunstige mogelijkheden.
In totaal zijn er 5 • 4 • 3 • 2 • 1 = 120 mogelijkheden om plaats te nemen.
De kans is dus  4/120 = 1/30
Maar de kans  is voor elke plaats even groot, dus de totale kans dat Bettie tussen Antonm en Connie zit is 5 • 1/30 = 1/6 

OF:
Voor de plaatsen naast Bettie moet je twee personen kiezen uit de 4. Dat kan op 4 nCr 2 = 6 manieren, dus de kans dat dat precies het tweetal Anton en Connie is is 1/6.
       
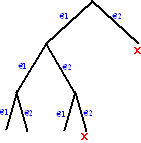
10. a. Zie de kansboom hiernaast
De takken met een rood kruis gaan fout, de rest gaat goed.

De kans is dan 0,5 • 0,5 • 0,5 • 3 =  3/8

       
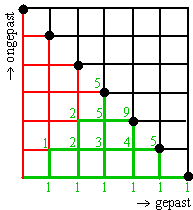
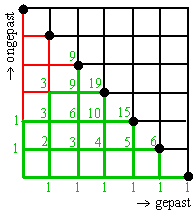
  b. Zie hiernaast.
Het aantal gepast moet steeds groter of gelijk aan het aantal ongepast zijn, dus mag je niet boven de diagonaal van dit rooster komen.
Dat geeft de groene routes hiernaast. De roden zijn foute routes.
Aan de groene getallen zie je dat er 5 + 9 + 5 + 1 = 20 toegestane routes zijn van de 26 = 64 in totaal.

De kans is dus 20/64 dat er geen wisselproblemen zijn

       
  c. Met twee losse euro's bij zich schuift de hele groene figuur 2 hokjes omhoog.

Ni zijn er 9 + 19 + 15 + 6 + 1 = 50 van de 64 goed.

De kans dat er geen wisselproblemen zijn is  50/64

       
11. a. P(PPP) = 2/6 • 2/6 • 2/6 = 1/27  
       
  b. P(CCC) = 1/6 • 1/6 • 1/6 = 1/216
P(PPP) = 2/6 • 2/6 • 1/6 = 4/216
P(KKK) = 3/6 • 2/6 • 2/6 = 12/216
       
  c. De kans op geen geld is per keer  1 - 0,005 - 0,019 - 0,056 = 0,92

P(25) = P(25-0) + P(0-25) + P(10-15) + P(15-10)
= 0,005 • 0,92 + 0,92 • 0,005 + 0,056 • 0,019 + 0,019 • 0,056 =  0,0113
       
  d. 25 • 0,005 + 15 • 0,019 + 10 • 0,056 + 0 • 0,92 = €0,97
       
12. a. P(Italiλ wint) = P(Italiλ raak en Nederland mis) = 0,82 • 0,37 = 0,3034
P(Nederland wint) = P(Nederland raak en Italiλ mis) = 0,63 • 0,18 = 0,1134
P(geen beslissing) = 1 - 0,3034 - 0,1134 = 0,5832
     
  b. P(Italiλ wint na 1 serie) = 0,30
P(Italiλ wint na 2 series) = 0,58 • 0,30 = 0,174
P(Italiλ wint na 3 series) = 0,58 • 0,58 • 0,30 = 0,10092
Samen geeft dat kans  0,30 + 0,174 + 0,10092 = 0,5749
     
  c. P(Nederland wint ) =
0,11 + 0,58 • 0,11 + 0,582 • 0,11 + 0,583 • 0,11 + 0,584 • 0,11 + .........
Noem deze kans K

K        =  0,11 + 0,58 • 0,11 + 0,582 • 0,11 + 0,583 • 0,11 + 0,584 • 0,11 + .........
0,58K =             0,58 • 0,11 +  0,582 • 0,11 + 0,583 • 0,11 + 0,584 • 0,11 + 0,585 • 0,11.........
K - 0,58K = 0,11
0,42K = 0,11
K = 0,11/0,42 = 0,2619
     
13. Stel dar er 2n knikkers in de vaas zitten.

P(2 roden MET terugleggen) = binompdf(4, 0.5, 2) = 0,375        (of  0,54 • (4 nCr 2))

P(2 roden ZONDER terugleggen) = (4 nCr 2) • n/2n • (n - 1)/(2n - 1) • n/(2n - 2) • (n -1)/(2n - 3)

Voer die laatste kans in bij Y1 van de GR en kijk bij TABLE wanneer dat minder dan 0,385 is

Dat geeft n = 39 dus bij 78 knikkers in de vaas
     
14. Leg de 36 niet-plaatjes op een rij.  Dat kan op 36! = 3,72 • 1041 manieren.
Dan zijn er 37 plaatsen waar een plaatje kan komen (de tussenruimtes en voor en achteraan)
Daaruit kun je op 37 nCr 16 = 1,29 • 1010  een groepje van 16 kiezen waar de plaatjes komen.
De 16 plaatjes kun je tenslotte op 16! = 2,09 •1013 manieren op die plekken leggen.
Samen geeft dat  3,72 • 1041 • 1,29 • 1010 • 2,09 • 1013 = 1,00 • 1064  manieren.

Zonder voorwaarden zijn er in totaal  52! = 8,07 • 1067 manieren om een rij te maken.

De kans op een gunstige rij is dan  (1,00 • 1064) / (8,07 • 1067 ) =  0,12 • 10-3 = 0,00012  
     
15. a. bekijk 1000 gevallen:
     
   
  wel gevangen niet gevangen  
mannetje 240 60 300
vrouwtje 455 245 700
  695 305 1000
     
    Van de 305 niet-gevangen vliegen waren er 60 bij een mannetje. De kans is dus 60/305 = 0,1967
     
  b. P(eerste 10 allemaal gevangen) = 0,810 = 0,1074
De kans op een luie kameleon is dus 0,1074 en de kans op een actieve kameleon is 1 - 0,1074 = 0,8926

P(11e vangen) = P(eerste 10 allemaal EN 11e) + P(eerste 10 niet allemaal EN 11e)
=  0,1074 • 0,40 + 0,8926 • 0,80 = 0,7570
     
16. a.
     
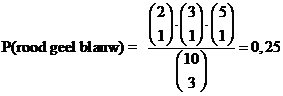    P(ιιn kleur niet) = P(niet rood) + P(niet geel) + P(niet blauw)
   
     
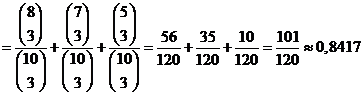  b. P(niet alle kleuren) = 1 - 1/4 = 3/4
Dit is binomiaal verdeeld.
n = 50
p = 3/4
P(X ≤ 30) = binomcdf(50, 0.75, 30) = 0,0139
     
  c. De laatste knikker ligt steeds vast: dat moet een rode zijn.
Van de overige knikkers moet er dan nog ιιn rode zijn, en de rest niet-rood
Dat geeft de volgende kansen:
   
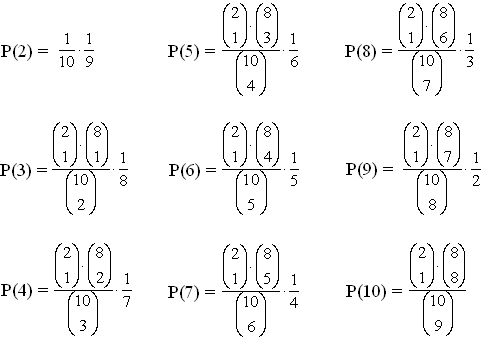    uitrekenen geeft deze kansverdeling:
     
   
R 2 3 4 5 6 7 8 9 10
P 0,0111 0,0444 0,0667 0,0889 0,1111 0,1333 0,1556 0,1778 0,2000
     
17. a.
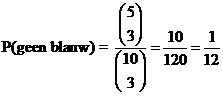    Kan op vier keer geen blauw (van de 10 keer)  is dan  binompdf(10, 1/12, 4) = 0,0060
     
  b. Als er evenveel gele als rode achterblijven is er ιιn gele meer dan rode getrokken.
Dat kan op 2 manieren :  (2 gele, 1 rode, 1 blauwe)  of  (1 gele, 0 rode, 3 blauwe)
   
     
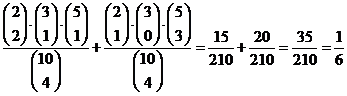  c. P(3 geel, 3 rood, 4 blauw)
= 0,23 • 0,33 • 0,54 • (10 nCr 3) • (7 nCr 3)
= 0,0567
     
18. a. P(som kleiner dan 11)
= P(123 of 124 of 125 of 126 of 127 of 234 of 235)  en dat zijn 7 mogelijkheden.
In totaal zijn er 12 nCr 3 = 220 mogelijkheden
De kans is daarom  7/220
     
  b. Voor 3 opeenvolgende nummers zijn er n - 2 mogelijke drietallen.
in totaal zijn er  (n  nCr 3) drietallen
de kans is dan  (n - 2)/(n  nCr 3)
Invoeren in de GR bij Y1 en dan bij TABLE kijken wanneer 0,01 is. 
Dat geeft  n = 25

Maar in 1984 deden ze dat vast algebraοsch!! Dat gaat zσ:
   
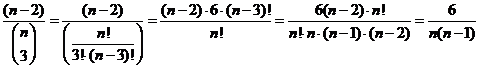    Als dat 1/100 is, dan is  600 = n (n - 1)
n2 - n - 600 = 0
(n - 25)(n + 24) = 0
n = 25   (of n = -24 maar die valt af)
     
  c.
   
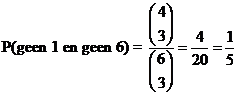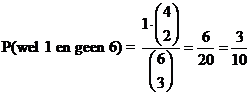    van de vijf keer moet de eerste 2 keer voorkomen en de tweede 3 keer.
Dat geeft kans  (1/5)2 • (3/10)3 • (5 nCr 2) = 0,0108
     
19. a. Voor de 5 witten zijn er 45 nCr 5 = 1221759 mogelijkheden
Voor de rode zijn er 45 mogelijkheden
In totaal zijn er 45 • 1221759 = 54979155 mogelijkheden waarvan er maar ιιn goed is.
     
  b. De kans zou 1 op 45 zijn bij de voorwaarde dat alleen de rode bal goed is.
     
  c. 0,3082 • x = 190000000  geeft  x = 616.482.803  dus ruim 616 miljoen formulieren.
     
  d. verwachtingswaarde per ingevuld formulier (zonder de jackpot):
100000 • 1/1249526 + 5000 • 1/274896 + 100 • 1/6248 + 100 • 1/7049 + 5 • 1/160 + 5 • 1/556 + 2 • 1/120 + 1 • 1/84 =
= 0,1972248 en dat is inderdaad ongeveer 19,72%
     
  e. P(prijs) = 1/54979155 + 1/1249526 + 1/274896 + 1/6248 + 1/7049 + 1/160 + 1/556 + 1/120 + 1/84 = 0,0286
Het aantal prijzen is binomiaal verdeeld.
n = 104
p = 0,0286
P(X > 1) = 1 - P(X ≤ 1) = 1 - binomcdf(104, 0.0286, 1) = 0,8013
     
20. a. Het aantal beschimmelde sinaasappels is binomiaal verdeeld met n = 3 en p = 0,01
P(1 beschimmeld) = binompdf(3 , 0.01 , 1) = 0,029

OF
Noem B = beschimmeld (kans 0,01)  en N = niet-beschimmeld (kans 0,99)
1 beschimmeld kan bijv. via de serie BNN en de kans daarop is  0,01 • 0,992
Er zijn  3 nCr 1 = 3 zulke series, dus de totale kans wordt  3 • 0,01 • 0,992 = 0,029
     
  b. Het aantal beschimmelde sinaasappels in een doos is binomiaal verdeeld met n = 50 en p = 0,01
De kans op en doos zonder beschimmelde sinaasappels is dan binompdf(50 , 0.01 , 0) = 0,605

OF
Dan moeten alle sinaasappels goed zijn en de kans daarop is  0,9950 = 0,605
     
  c. De kans op een doos die niet in orde is is  1 - 0,605 = 0,395.
Het aantal dozen dat niet in orde is is binomiaal verdeeld met n = 5 en p = 0,395.
P(X ≥ 4) = 1 - P(X ≤ 3) = 1 -binomcdf(5 , 0.395 , 3) = 1 - 0,917 = 0,083
     
21. a. Gemiddeld zal hij per 26 flesjes ιιn gratis flesje krijgen.
Dus 10 gratis flesjes bij gemiddeld 260 flesjes.
     
  b. De kans op een P is  1/26,  dus de kans op geen P is  25/26.
De kans op  niet P - niet P - wel P  is dan  (25/26)•(25/26)•(1/26) » 0,036
     
  c. Het aantal kurken met een P is binomiaal verdeeld met  n = 10  en  p = 1/26
P(X ³ 1) = 1 - P(X = 0) = 1 - binompdf(40 , 1/26 , 0) = 1 - 0,67556... = 0,32443...  dus ongeveer 0,324
(Je kunt de kans op  X = 0  natuurlijk ook uitrekenen door  (25/26)10 te berekenen)
     
  d. De kans op precies de volgorde  P-I-L-S is  (1/26)•(1/26)•(1/26)•(1/26)
Er zijn  4•3•2•1 = 24 zulke volgorden te maken.
De totale kans wordt dus 24 • (1/26)4 = 0,000053... en dat is ongeveer 0,0053%

OF
De kans op een goede letter bij de eerste kurk is  4/26
De kans op een goede letter bij de tweede kurk is  3/26
De kans op een goede letter bij de tweede kurk is  2/26
De kans op een goede letter bij de tweede kurk is  1/26
De totale kans wordt dan  (4/26)•(3/26)•(2/26)•(1/26) = 0,000053... en dat is ongeveer 0,0053%
     
22. a. Binomiaal met  n = 50,  p = 0,08
P(X ≥ 8) = 1 - P(X ≤ 7) = 1 - binomcdf(50, 0.08, 7) = 0,04379
     
  b. P(linkerzij-rechterzij) + P(rechterzij-linkerzij) = 0,29 • 0,35 + 0,35 • 0,29 = 0,20
     
  c. P(punten kwijt) = 0,20
P(punten niet kwijt) = 1 - 0,20 = 0,80
P(niet-niet-niet) = 0,80 • 0,80 • 0,80 » 0,5
     
  d. De volgende kansboom geldt:
   

    De behaalde punten zijn zwart, de kansen blauw.
a:  P(linkerzij-linkerzij) + P(rechterzij-rechterzij) = 0,29 • 0,29 + 0,35 • 0,35 = 0,2066
b:  1 - 0,20 - 0,2066 = 0,5934
De rode takken leveren winst op:
0,5934 + 0,2066 • 0,8 = 0,75868
     
23. a. P(MMMV) = 8/16 • 7/15 • 6/14 • 8/13 = 4/65
Er zijn  4 nCr 1 = 4  zulke mogelijke volgorden, dus de totale kans is 4 • 4/65 = 16/65
     
  b. Dan moet speler 1 vier wedstrijden winnen: kans (1/2)4 = 1/16
verder moet speler 2 de eerste drie wedstrijden winnen: kans (1/2)3 = 1/8
Samen geeft dat een kans van  1/16 • 1/8 = 1/128
     
  c.
aantal wedstrijden 1 2 3 4
kans 1/2 1/2 • 1/2 = 1/4 1/2 • 1/2 • 1/2 = 1/8 1/2 • 1/2 • 1/2 = 1/8
     
    De verwachtingswaarde is dan  1 • 1/2 + 2 • 1/4 + 3• 1/8 + 4 • 1/8 = 1,875

of:
Er worden 8 + 4 + 2 + 1 = 15 wedstrijden gespeeld, dus wordt 30 keer door iemand een wedstrijd gespeeld.
Er zijn 16 deelnemers, dus gemiddeld is dat 30/16 = 1,875 wedstrijden per persoon.

     
  d. Stel V het aantal vrouwen dat wint, en g het grensgetal waarnaar we opzoek zijn;
P(V ≥ g , n = 52, p = 1/2) < 0,05
1 - P(V ≤ g - 1) < 0,05
Voer dus in Y1 = 1 - binomcdf(52, 0.5, X - 1) en kijk met TABLE wanneer de waarde voor het eerst kleiner is dan 0,05. Dat is bij X = 33 (P = 0,0352)
Dus 33 of meer vrouwelijke winnaars wordt abnormaal hoog gevonden.
     
24. a. Het aantal  fout beantwoorde vragen is binomiaal verdeeld met n = 10 en p = 0,2
P(X ≥ 1) = 1 - P (X ≤ 0) = 1 - binomcdf(10, 0.2, 0) = 0,8926
     
  b. Stel dat er drie antwoorden zijn waarvan A het goede is.
P(A) = 0,8  en  P(B) = P(C) = 0,1
Dan is  P(AA) + P(BB) + P(CC)  = 0,82 + 0,12 + 0,12 = 0,66
     
  c. P(1 vraag hetzelfde) = 0,66  (zie vraag 9)
P(10 vragen hetzelfde) = 0,6610 = 0,0157
Dat is niet kleiner dan 1% dus de docent zal geen strafmaatregelen treffen.
     
25. a. Omdat het aantal M&M heel groot is zal het feit dat er al eentje is getrokken niet veel invloed hebben op de kansen bij de volgende M&M. Die kansen zullen ongeveer gelijk blijven.
     
  b. n = 50
p = 0,20
P(X = 10) = binomdf(50, 0.20, 10) = 0,1398
     
  c. vaasmodel: er zijn 10 blauwen en 40 niet-blauwen.
   
     
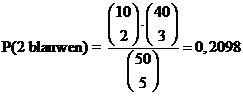26. a. Dit is een vaasmodel.
Er zijn 28 bloemkoolkaarten en 84 andere kaarten.
     
       
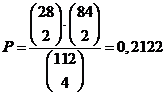  b. Het aantal keren de de eerste kaart een tomaat is, is binomiaal verdeeld.
n = 150, p = 0,25
P(X > 37) = 1 - P(X ≤ 37) = 1 - binomcdf(150, 0.25, 37) = 0,4937
       
27. a. P(meedoen) = P(6) + P(345 en dan 6) + P(345 en dan 345 en dan 6)
= 1/6 + 1/2 • 1/6  + 1/2 • 1/2 • 1/6 = 7/24
       
  b. 7/24 • (17/24)3 = 0,1037  
       
  c. Hij wint 4 euro als niemand wint:  kans  (17/24)4 = 0,2517
Hij wint niets als er wel iemand iets wint:  kans  1 - 0,2517 = 0,7483

Gemiddelde winst is  4 • 0,2517 + 0 • 0,7483 = €1,01
       
  d. P(1) = P(6 of 12) = 1/2
P(2) = P(345 en dan 126) = 1/2 • 1/2 = 1/4
P(3) = P(345 en dan 345) = 1/2 • 1/2 = 1/4

Gemiddelde:   1 • 1/2 + 2 • 1/4 + 3 • 1/4 = 1,75
       
28. a. P(ABC) = 0,50 • 0,30 • 0,20 = 0,03
er zijn 6 zulke volgorden mogelijk , dus de kans is 6 • 0,03 = 0,18.
       
  b. minstens dan 10:   AAA of AAB
de kans daarop is 0,5 • 0,5 • 0,5 + 3 • 0,5 • 0,5 • 0,3 = 0,35
P(minder dan 10) = 1 - 0,35 = 0,65
       
  c. de verwachtingswaarde:   0,5 • 4 + 0,3 • 2 + 0,2 • 1 = €2,80
       
  d. bninomiaal m,et n = 100, p = 0,2
P(X > 25) = 1 - P(X ≤ 24) = 1 - binomcdf(100, 0.2, 24) = 0,1314
       
29. a. Voor €80  moet je 2 briefjes van €20 en 4 briefjes van €10 pakken

Methode 1.
per portemonnee is de kans op €20 gelijk aan 4/16 = 1/4
De kans op 2 van de zes is dan  binompdf(6, 1/4, 2) = 0,8306

Methode 2.
dit is een vaasmodel.

   
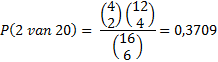    Het verschil is  0,8306 - 0,3709 = 0,4597
       
  b. Uit ιιn portemonnee kun je  20 of 30 of 40 euro halen.
     
   

   

    P(40) = 1 - 0,55 - 0,40 = 0,05  
       
    Voor de drie portemonnees geldt nu:
P(80 totaal) = P(20, 20, 40) + P(30, 30, 20)
= 3 • 0,55 • 0,55 • 0,05  +  3 •  0,40 • 0,40 • 0,55 = 0,3094
       
30. a. Hij krijgt minstens 8 roebel als hij begint met 3 keer kop.
P(kkk) = 1/2 • 1/2 • 1/2 = 1/8
De rest doet er niet toe..
       
  b. P(minstens ιιn keer) = 1 - P(nooit) = 1 - P(Niet, Niet, Niet, Niet)
= 1 - 7/8 • 7/8 • 7/8 • 7/8 = 1659/4096 = 0,4138
       
  c. P(1) = P(k) = 1/2
P(2) = P(km) = 1/2 • 1/2 = 1/4
P(8) = P(kkkm) = 1/2 • 1/2 • 1/2 • 1/2 = 1/16

P(1-1-2-8) = 1/2 • 1/2 • 1/4 • 1/16 = 1/256
Maar dat kan op  (4 ncr 2) • 2 = 12 volgorden.
De totale kans is dus  12/256 = 3/64 = 0,046875
       
  d. na ιιn keer kop  21 = 2 roebel
na 2 keer kop  22 = 4 roebel
.....
na 10 keer kop  210 = 1024 roebel
na 11 keer kop  211 = 2048 roebel
na 12 keer kop  212 = 4096 roebel
na 13 keer kop  213 = 8192 roebel.

er moet dus 13 keer kop worden gegooid.
de kans daarop is  (1/2)13 = 1/8192 = 0,000122
       
  e.
uitkomst m km kkm kkkm kkkkm kkkkk
uitbetaling 1 2 4 8 16 0
kans 1/2 1/4 1/8 1/16 1/32 1/64
             
    gemiddelde:  1 • 1/2 + 2 • 1/4 + 4 • 1/8 + 8 • 1/16 + 16 • 1/32 + 0 • 1/64 = 2,5 roebel.
       

© h.hofstede (h.hofstede@hogeland.nl)